平时二十三测

昨日AK，今日垫底，我简直是在坐过山车；

以后记住有返回值的函数一定要写返回值，不然全部输出0

题解:

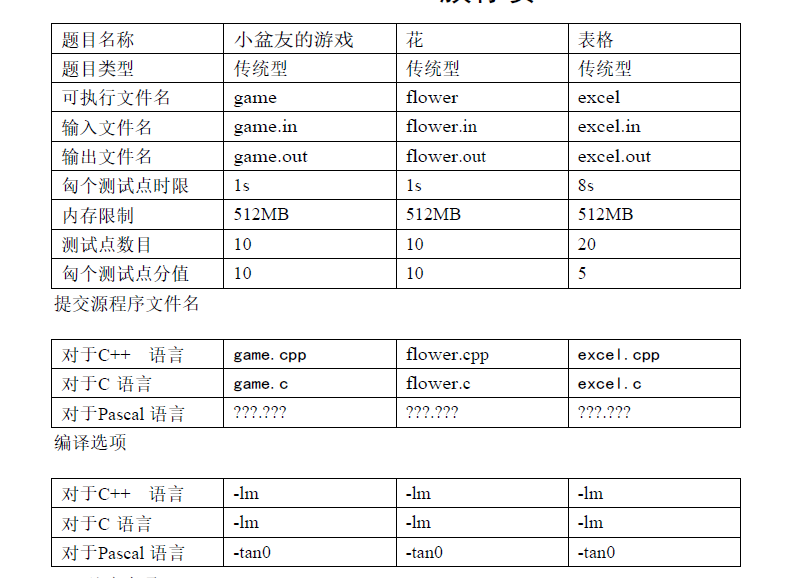
第一题：全是-1，是2^(n-1)-1,不会证，样例很明显；

对于有X个跟班的人，设它的期望函数f(X)=2^X-1；

利用期望的线性性，Ｅ（Ａ）＋Ｅ（Ｂ）＝Ｅ（Ｃ），则Ｅ（Ｂ）＝Ｅ（Ｃ）－Ｅ（Ａ）；

Ｅ（Ｃ）＝初始都是－１的局面到之剩一个人；

Ｅ（Ａ）＝当前到只剩一个人；

求Ｅ（Ｂ）就直接用打表的规律；整个局面的期望函数值为：所有人期望函数值之和。

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int M = 1e6 + 5;
int cnt[M], bin[M];
const int mod = 1e9 + 7;int main(){freopen("game.in","r",stdin);freopen("game.out","w",stdout);int n, u;scanf("%d", &n);for(int i = 1; i <= n; i++){scanf("%d", &u);if(u != -1) cnt[u]++;}bin[0] = 1;for(int i = 1; i <= n; i++) bin[i] = (bin[i-1]<<1) % mod;int ans = bin[n-1] - 1;for(int i = 1; i <= n; i++)ans = (ans - (bin[cnt[i]]-1) + mod) % mod;printf("%d\n", ans);
}

View Code

第二题：ｄｐ［ｉ］［０／１］［０／１］　一维表示考虑到第ｉ个数，二维表示前一个数是否与当前一样，三维表示是否已经合法，

转移就像扫雷一样用中间的转移；

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int M = 1e6 + 10;
const ll mod = 1e9 + 7;
#define RG register
ll dp[M][2][2];int main(){freopen("flower.in","r",stdin);freopen("flower.out","w",stdout);//int cc=clock();int T;scanf("%d", &T);while(T--){int L, S;scanf("%d%d", &L, &S);memset(dp, 0, sizeof(dp));dp[1][0][0] = S;int u = 0;for(RG int i = 1; i < L; i++){dp[i+1][0][0] = (dp[i+1][0][0] + dp[i][0][0]*(S-1)%mod)%mod;dp[i+1][1][0] = (dp[i+1][1][0] + dp[i][0][0])%mod;dp[i+1][0][1] = (dp[i+1][0][1] + dp[i][0][1]*(S-1)%mod)%mod;dp[i+1][1][1] = (dp[i+1][1][1] + dp[i][0][1])%mod;dp[i+1][0][0] = (dp[i+1][0][0] + dp[i][1][0]*(S-1)%mod)%mod;dp[i+1][1][1] = (dp[i+1][1][1] + dp[i][1][0])%mod;dp[i+1][0][1] = (dp[i+1][0][1] + dp[i][1][1]*(S-1)%mod)%mod;}ll ans = (dp[L][0][1] + dp[L][1][1]) % mod;printf("%lld\n",ans);}//int tt=clock();//fprintf(stderr, "%d\n", tt-cc);
}

View Code

第三题：利用扫描线算法，首先将所有坐标离散化，然后按照正方向枚举x坐标，每次求出当前这个横坐标能看见的某个矩形，将其标记并更新答案。直到这个横坐标所有能看见的矩形均被标号为止。

并且，将每个颜色的权值设为其操作的编号将每个矩形视作两条线段：矩形的左侧视为加入当前矩形，右侧+1的位置视为删去当前矩形。用线段树+set维护。对于每个线段树上的节点，存储两个值与一个set，分别设为maxv,minv,S

maxv表示：当前区间内能够看见的，编号最大的未被
标记的颜色。
 minv表示：当前区间内能看见的最小的颜色。（用于更
新maxv）
 S存储完全覆盖了当前区间的所有颜色。
 接下来是更新maxv和minv

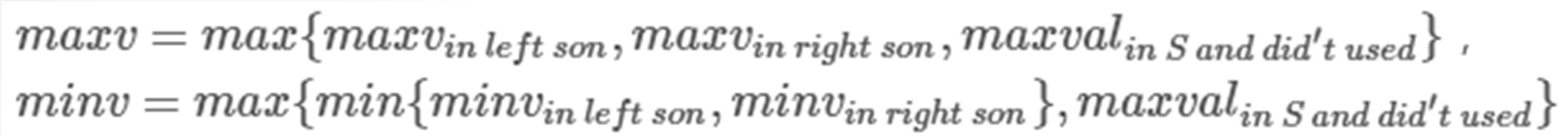
理解起来很容易，maxv的更新就不用说了，对minv的更新：里层的min就是左右区间内能看见颜色的最小值，而外层的max是因为：当前区间内都被这个值覆盖，所以取max。

然后，若maxv<minv，说明当前maxv这个颜色一定被其他已更新颜色覆盖掉了，因为它连当前区间内能看见的最小的值都不够。所以将maxv修正为-1，即记为当前区间不含可以被更新的颜色。

每更新一次，继续判断根节点的maxv是否为-1，若不是则继续标记，若是则停止。

Ｏ（ｎｌｏｇ＾２）

#include<bits/stdc++.h>
using namespace std;const int M = 6e5 + 5;int tox, toy, dx[M], dy[M], ls[M], rs[M], N;
bool used[M];struct query{int l, r, del, id, x;bool operator < (const query &rhs) const{if(x == rhs.x) return l < rhs.l;return x < rhs.x;}
}blo[M];void pushx(int x){dx[++tox] = x; dx[++tox] = x-1; dx[++tox] = x+1;
}
void pushy(int y){dy[++toy] = y; dy[++toy] = y-1; dy[++toy] = y+1;
}struct Node{int mx, mi;set <int> s;Node *ls, *rs;void up(){if(ls==NULL && rs==NULL){if(s.empty()){mi = mx = -1;return ;}mi = mx = *s.rbegin();if(used[mx]) mx = -1;}else {mi = min(ls->mi, rs->mi);mx = max(ls->mx, rs->mx);if(s.empty()) return ;int ins = *s.rbegin();mi = max(mi, ins);if(mx < ins){if(used[ins]) mx = -1;else {if(mi <= ins) mx = ins;else mx = -1;}}}}
}pool[M << 2], *tail = pool, *root;Node *build(int lf = 1, int rg = N){Node *nd = ++tail;nd->mi = nd->mx = -1;if(lf == rg) ;else {int mid = (lf + rg) >> 1;nd->ls = build(lf, mid);nd->rs = build(mid + 1, rg);}return nd;
}
#define Ls nd->ls, lf, mid
#define Rs nd->rs, mid+1, rg
void add(int L, int R, int opt, int d, Node *nd = root, int lf = 1, int rg = N){if(L <= lf && rg <= R){if(opt == 1) nd->s.insert(d);else nd->s.erase(d);nd->up();return ;}int mid = (lf + rg) >> 1;if(L <= mid) add(L, R, opt, d, Ls);if(R > mid) add(L, R, opt, d, Rs);nd->up();return ;
}void Update(int L, int R, Node *nd = root, int lf = 1, int rg = N){if(L <= lf && rg <= R){nd->up();return ;}int mid = (lf + rg) >> 1;if(L <= mid) Update(L, R, Ls);if(R > mid) Update(L, R, Rs);nd->up();return ;
}int read(){int x = 0; int f = 1; char c = getchar();while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();}while(c<='9'&&c>='0'){x=x*10+c-'0';c=getchar();}return x*=f;
}int main(){freopen("excel.in","r",stdin);freopen("excel.out","w",stdout);int n = read(), cnt = 0;for(int i = 1; i <= n; i++){int xl = read(), yl = read(), xr = read(), yr = read();xr--, yr--;blo[++cnt] = (query) {yl, yr, 1, i, xl};blo[++cnt] = (query) {yl, yr, -1, i, xr+1};pushx(xl); pushx(xr+1);pushy(yl); pushy(yr);}sort(dx + 1, dx + 1 + tox);sort(dy + 1, dy + 1 + toy);tox = unique(dx + 1, dx + 1 + tox) - dx - 1;toy = unique(dy + 1, dy + 1 + toy) - dy - 1;for(int i = 1; i <= cnt; i++){blo[i].x = lower_bound(dx + 1, dx + 1 + tox, blo[i].x) - dx;blo[i].l = lower_bound(dy + 1, dy + 1 + toy, blo[i].l) - dy;blo[i].r = lower_bound(dy + 1, dy + 1 + toy, blo[i].r) - dy;ls[blo[i].id] = blo[i].l, rs[blo[i].id] = blo[i].r;}sort(blo + 1, blo + 1 + cnt);int lst = 1;N = toy;root = build();for(int i = 1; i <= tox; i++){while(lst <= cnt && blo[lst].x == i){add(blo[lst].l, blo[lst].r, blo[lst].del, blo[lst].id);lst++;}while(root->mx != -1){int x = root->mx;used[x] = 1;Update(ls[x], rs[x]);}}int ans = 0;for(int i = 1; i <= n; i++) if(used[i]) ans++;printf("%d\n", ans+1);}