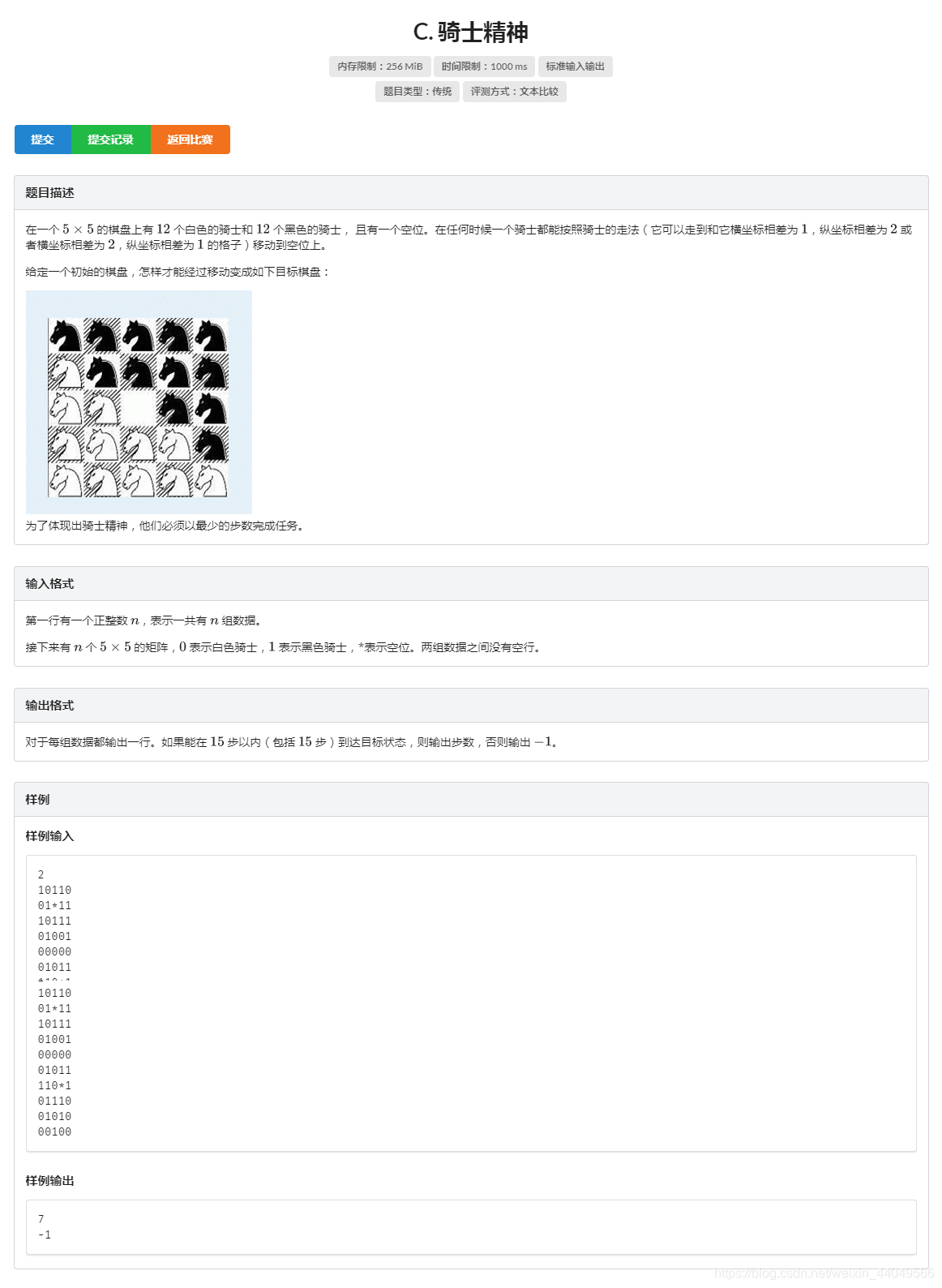
题目
此题根据题目可知是迭代加深搜索。
首先应该枚举空格的位置,让空格像一个马一样移动。
但迭代加深搜索之后时间复杂度还是非常的高,根本过不了题。
感觉也想不出什么减枝,于是便要用到了乐观估计函数(Optimistic Estimation Function)
以3种颜色的格子来表示原棋盘:
如果我们要从一个状态抵达到原棋盘,那么需要的步数绝对是小于当前状态与原棋盘不同的格子的数量、
那么我们的乐观估计函数就出来了。如果当前状态与原棋盘的不同格子数量小于我们的剩余的步数,那么肯定是抵达不了的,return回去就行。
代码
#include <iostream>
#include <cstring>
using namespace std;#define N 510int dir[8][2]={{2,1},{2,-1},{-2,1},{-2,-1},{1,2},{1,-2},{-1,-2},{-1,2}};
int fuck[10][10]={{0,0,0,0,0,0},{0,1,1,1,1,1},{0,0,1,1,1,1},{0,0,0,2,1,1},{0,0,0,0,0,1}};
int a[10][10],T,px,py,len,flag=0;int dif() {int sum=0;for(int i=1;i<=5;i++) for(int j=1;j<=5;j++)if(a[i][j] != fuck[i][j]) sum++;return sum;
}void dfs(int step) {if(step>len) {if(dif()==0) flag=1;return ;}if(dif()>len-step+2) return ;for(int k=0;k<8;k++) {int tx=px+dir[k][0],ty=py+dir[k][1];if( tx<1 || tx>5 || ty<1 || ty>5) continue;swap(a[tx][ty],a[px][py]);swap(px,tx);swap(py,ty);dfs(step+1);swap(a[tx][ty],a[px][py]);swap(px,tx);swap(py,ty);}
}int main() {cin>>T;while(T--) {flag=0;memset(a,0,sizeof(a)); for(int i=1;i<=5;i++) for(int j=1;j<=5;j++) {char l;cin>>l;if(l=='1') a[i][j]=1;else if(l=='0') a[i][j]=0;else a[i][j]=2,px=i,py=j;}for(len=0;len<=15;len++) {dfs(1);if(flag) {cout<<len<<endl;break;}}if(!flag)cout<<-1<<endl;}
}在我的程序里有这一句:
if(dif()>len-step+2) return ;因为有这种特例,保险起见,多加一个1。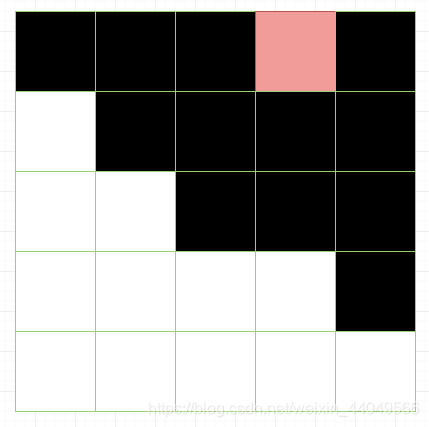






 (差分TLE))






之数组和切片)






