6-3 向二分搜索树中添加元素 6-4 改进添加操作：深入理解递归终止条件

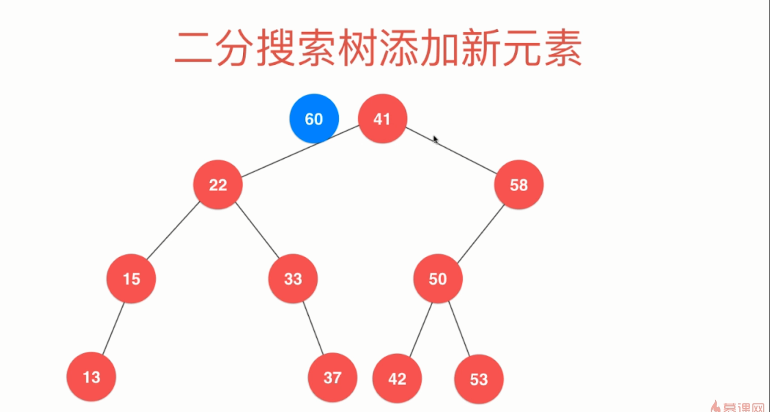
二分搜索树添加新元素60,

60>41(根节点)，所以一定要插入到41的右子树。

接着在和58比较

 

 

 

public class BST<E extends Comparable<E>> {//对于二分搜索树所存储的内容支持泛型，所以在这里写一个E，此外二分搜索树不是支持所有的类型，对这个类型必须要有限制,
    //这个限制是这个类型必须拥有可比较性，放到代码中，就必须对E进行限制，即E extends Comparable<E>（E要满足可比较性）

    private class Node {  //声明节点类
        public E e;  //节点可以存放元素e
        public Node left, right;  //成员变量

        public Node(E e) {  //node的构造函数，用户传来一个e
            this.e = e;   //this.e等于用户传来的e（用户传来的参数和节点类成员变量元素均用e表示，所以节点存放元素用this.e表示）
            left = null;
            right = null;
        }
    }
    //二分搜索树的成员变量root、size
    private Node root;  //root:根节点
    private int size;  //size:记录二分搜索树存储了多少元素

    public BST(){    //二分搜索树的构造函数
        root = null;  //初始化时二分搜索树一个元素也没有存，根节点root为空
        size = 0;
    }

    public int size(){
        return size;
    }

    public boolean isEmpty(){
        return size == 0;
    }

    // 向二分搜索树中添加新的元素e
    public void add(E e){

        if(root == null){
            root = new Node(e);
            size ++;
        }
        else
            add(root, e);
    }

    // 向以node为根的二分搜索树中插入元素e，递归算法
    private void add(Node node, E e){
        //-------------递归的终止条件-------------------//
        if(e.equals(node.e))    //先检查一下要插入的元素e是否等于node的e，如果等于的话，其实就等于我们要插入的元素在二分搜索树中已经有啦。对于这种情况直接return
            return;
        else if(e.compareTo(node.e) < 0 && node.left == null){ //否则，如果要插入的e小于根节点node的e，且node的左子树为空，插入node的左子树
            node.left = new Node(e);
            size ++;
            return;
        }
        else if(e.compareTo(node.e) > 0 && node.right == null){
            node.right = new Node(e);
            size ++;
            return;
        }
        //-------------递归的终止条件----结束---------------//

        //--------------递归调用------------------//
            //如果没有在递归的终止条件成功的return回去的话，就会根据二分搜索树固有的递归结构来看是向节点的左子树插入元素e还是向节点的右子树插入元素e
        if(e.compareTo(node.e) < 0)//如果要插入的e小于根节点node的e
            add(node.left, e);
        else //e.compareTo(node.e) > 0
            add(node.right, e);
    }
}

 

对于二分搜索树的插入操作现在这么写是比较复杂的，在下一小节将改进代码，算法没有变化，但会让代码简洁很多。通过下一节，会让大家体会对于递归算法来说，一方面有不同是写法，另一方面终止条件也会有不同的考量。

 

6-4 改进添加操作：深入理解递归终止条件

 这个递归函数的终止条件非常的臃肿，因为要考虑它的左孩子是不是空、右孩子是不是为空

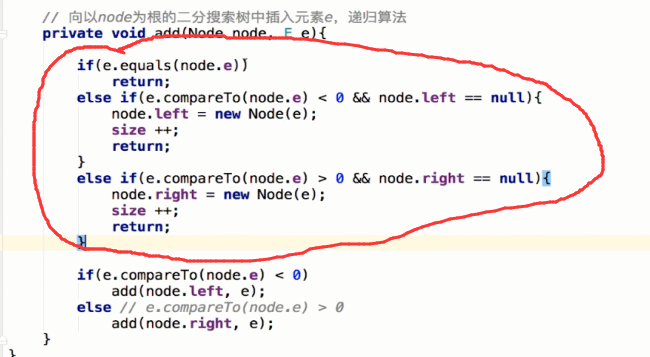
事实上，空本身也是一颗二叉树，如果二叉树为空的话，此时肯定要插入一个节点，

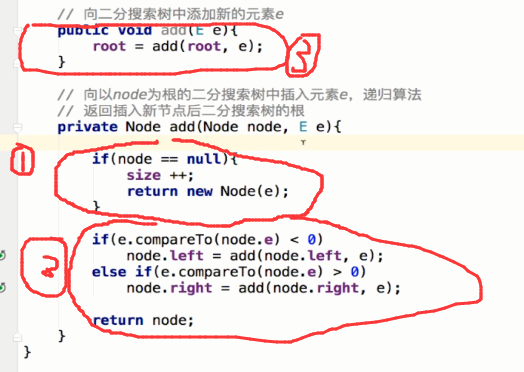
完整代码如下：

public class BST<E extends Comparable<E>> {

    private class Node {
        public E e;
        public Node left, right;

        public Node(E e) {
            this.e = e;
            left = null;
            right = null;
        }
    }

    private Node root;
    private int size;

    public BST(){
        root = null;
        size = 0;
    }

    public int size(){
        return size;
    }

    public boolean isEmpty(){
        return size == 0;
    }

    // 向二分搜索树中添加新的元素e
    public void add(E e){
        root = add(root, e);
    }

    // 向以node为根的二分搜索树中插入元素e，递归算法
    // 返回插入新节点后二分搜索树的根
    private Node add(Node node, E e){
        if(node == null){
            size ++;
            return new Node(e);
        }
        //不管是左子树插入元素还是右子树插入元素，插入完成后，都将当前node的左孩子node.left 、右孩子node.right进行重新赋值，node也会得到更新，最后return node;，返回插入新节点后二分搜索树的根
        if(e.compareTo(node.e) < 0)
            node.left = add(node.left, e);
        else if(e.compareTo(node.e) > 0)
            node.right = add(node.right, e);

        return node;
    }
}