由于时间比较充裕，重新修订一部分。
这次把一些补充的放进来，其他的基础说明见后半部分
这些一共说明：01背包、完全背包、多重背包 将会详细说明。
三种背包混合、二维背包、分组背包、依赖背包、泛化背包 将大致说明。
01背包
如上次说明一般，这次提一下优化和其他说明
首先我做01背包的思路的是在背包价值固定的情况下，不断遍历增加物品，获取当前背包容量下课存放的最大价值
同时也有另一种做法：物品固定，遍历背包大小，获取该物品存放与否对总价值的影响。
后一种肯能优化更高一点 但不会太多，两者复杂度都是O(VN)
其中时间复杂度无法优化，但空间复杂度可以进行简单优化到O(N)
因为创建二维数组的目的是为了记录中间变量，每次记录当前行的值，下一次循环的时候与上一次的值进行比较。
那么就可以优化为以为一维数组，数组记录当前行的值，下一次循环的时候倒序判断，因为每次判断的值是上一行对应的值和上一行列数靠前的值加上物品的价值。
倒序遍历的时候可以把值进行覆盖更新，以便以后多次更新利用。
下面放上代码吧：
1 For(int i= 0, i<N; i++ ){ 2 for(int j = U; j>Ti; j--}{ 3 F[j] = Max(F[j], f[j-Ti]+Vi) 4 } 5 }
同样的需要进行初始化赋值。
这里提一下，之前以为赋值为0就好了，后来发现在大神们的思想里又对问题进行了细分
包括1.只求出最大价值，不要求必须袋子放满 2.恰好装满背包时最大价值
是不是感受到大神们满满的恶意
下面用原话来进行解释（我怕我解释不清楚）
我们看到的求最优解的背包问题题目中，事实上有两种不太相同的问法。有的题目
要求“恰好装满背包”时的最优解，有的题目则并没有要求必须把背包装满。一种区别
这两种问法的实现方法是在初始化的时候有所不同。
如果是第一种问法，要求恰好装满背包，那么在初始化时除了F[0] 为0，其它
F[1::V ] 均设为?1，这样就可以保证最终得到的F[V ] 是一种恰好装满背包的最优解。
如果并没有要求必须把背包装满，而是只希望价格尽量大，初始化时应该将F[0::V ]
全部设为0。
这是为什么呢？可以这样理解：初始化的F 数组事实上就是在没有任何物品可以放
入背包时的合法状态。如果要求背包恰好装满，那么此时只有容量为0 的背包可以在什
么也不装且价值为0 的情况下被“恰好装满”，其它容量的背包均没有合法的解，属于
未定义的状态，应该被赋值为-∞ 了。如果背包并非必须被装满，那么任何容量的背包
都有一个合法解“什么都不装”，这个解的价值为0，所以初始时状态的值也就全部为0
了。
完全背包
下面说一下完全背包，完全背包就是说物品的个数无限个，可以重复放置
这样就要求比较的时候不能与上一个相比，于是状态转移方程式就改为与当前行进行比较
valueData[i][j] = Max(valueData[i-1][j], valueData[i][j-weight[z]]+value[z]);
与01背包的区别是
因为物品存放无个数限制，完全可以多次放置，所以比较对象是当前物品放置历史最优值和不放置当前物品。
如此则完成完全背包的实现。
同样的 完全背包也可以进行空间复杂度的优化，原理与01背包相同。
多重背包
多重背包的定义是物品个数有限个，并且说明当前物品个数。
状态转移方程式
1 valueData[i][j] = Max ( valueData[i-1][j - k*weight[i]] +k*value[i] ) 0<=k<=num[i] 解释起来就是物品放置个数内求出最大价值
混合三种背包
字面意思，三种背包都存在的混合体，有的物品只有一个（01背包），有的物品无限多个（完全背包）
有的物品有限多个（多重背包），这是可以将问题划为三分，分别把之前的背包封装起来，判断物品是哪一类分别调用不同的方法
最终求得最优解
二维背包
物品的属性有两个，要同时满足才可放进去，例如袋子存放物品既要考虑物品体积也要考虑物品重量
对应解决办法是创建的数组也增加维度，
详细的。。。。。不会
分组背包
意思多个物品被分组，且分组内物品相互排斥，只能取出一个
详细。。。。。不会
泛化背包
意思是物品没有固定价值和质量，物品的价值和质量随着分配的空间变化 ，。。。。。。不会
感觉就像液体水一样，好几种水，每个都是泛化对象，但又感觉不会这么简单。。。是在搞不懂大神们是怎么思考问题的
OVER
背包问题说起来就是不断的在基础上提出新的问题，再不断解决、不断提问题
然后大神们津津乐道，我却疯掉了。。
以下是上次分享的内容
第一次分享，并不知道该拿出些什么，之前学的算法好像都还回去了。
最后祭出了背包，可是背包九讲又不全会，于是拿出了最简单的01背包。
话说。。。。01背包也忘了
开始复习ing。
1.01背包
首先01背包是对一个有固定容积的“”盒子“”进行物品存放，有N个物品，
每个物品的价值、体积分别是V1/T1、V2/T2、、、Vn/Tn。
需要求出能存放的最大价值。
按照固有思想，肯定放置性价比最高的，但是存在容积不匹配的情况
随便一个反例，有一个价值10、体积5和一个价值1体积1的物品，放在容量为4的袋子中。
如果选择倒推，则变成了暴力搜索了，时间复杂度就变大了。
在此基础上，机智的前辈们用贪心思想，加上动态规划完成了01背包。
将一个大问题的最优解，分解成一堆堆小问题的最优解，
要求得能放置的最大价值，对于每个物品求出放与不放的最优解。
例如对第i个物品，在能够放置的前提下，求出放这个物品和不放这个物品的最优值。
得到状态转移方程式：
F[i][j] = Max(F[i-1][j], F[i-1][j-Ti]+Vi);
举例说明：
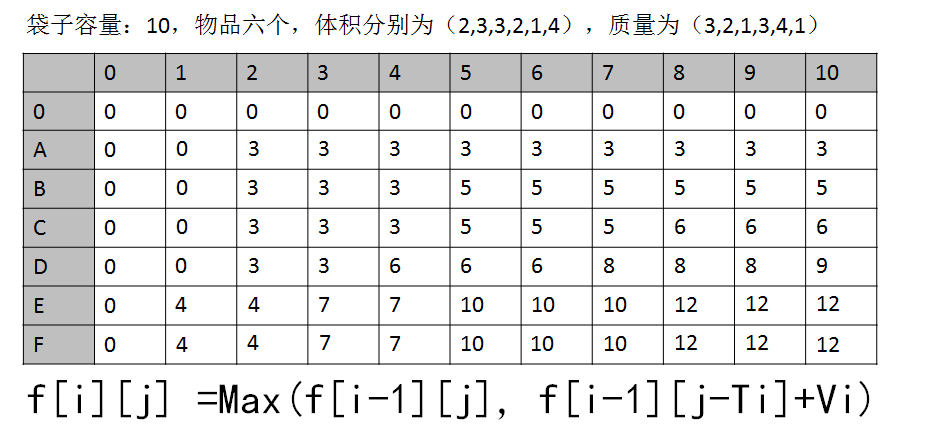
两个0的初始化是为了放置数组越界出现异常。
完全背包、多重背包的拓展
完全背包：在01背包的基础上，每个物品可以无限制存放个数。
状态转移方程式改成与F[i][j-Ti]+Vi。
多重背包：在01背包基础上，每个物品可以放置有限次数且不固定。
01背包中存在价值体积相同的物品，可以转化为01背包思考。
剩下的几种，不会。。。。
