拉格朗日乘子法 (Lagrange multipliers)是⼀种寻找多元函数在⼀组约束下的极值的⽅法。

通过引⼊拉格朗⽇乘⼦，可将有 d 个变量与 k 个约束条件的最优化问题转化为具有 d + k 个变量的⽆约束优化问题求解。

本⽂希望通过⼀个直观简单的例⼦尽⼒解释拉格朗⽇乘⼦法和KKT条件的原理。以包含⼀个变量⼀个约束的简单优化问题为例。如图所示，我们的⽬标函数是f(x) = x + 4x − 1，讨论两种约束条件g(x)：

1. 在满⾜x≤−1 约束条件下求⽬标函数的最⼩值；
2. 在满⾜ x≥−1约束条件g(x)下求⽬标函数的最⼩值。

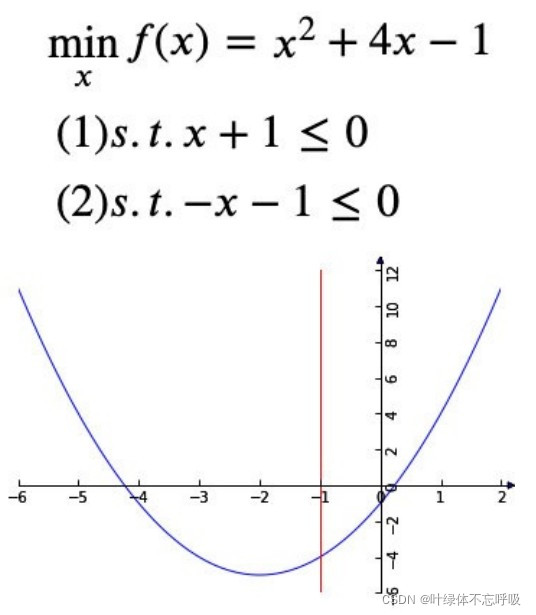
我们可以直观的从图中得到，
对于约束 1) 使⽬标值f(x)最⼩的最优解是x=−2；
对于约束 2) 使⽬标值f(x)最⼩的最优解是x=−1。

下⾯我们⽤拉格朗⽇乘⼦来求解这个最优解。

当没有约束的时候，我们可以直接令⽬标函数的导数为0，求最优值。
可现在有约束，那怎么边考虑约束边求⽬标函数最优值呢？

最直观的办法是把约束放进⽬标函数⾥，由于本例中只有⼀个约束，所以引入⼀个朗格朗⽇乘⼦λ，构造⼀个新的函数，拉格朗⽇函数h(x)，h(x) = f(x) + λg(x)。

该拉格朗⽇函数h(x)最优解可能在g(x)<0区域中，或者在边界g(x)=0上，下⾯具体分析这两种情况，当g(x)<0时，也就是最优解在g(x)<0区域中， 对应约束1) x≤−1的情况。此时约束对求⽬标函数最⼩值不起作⽤，等价于λ=0，直接通过条件∇ॖ(१∗)=0，得拉格朗⽇函数h(x)最优解x=−2。当g(x)=0时，也就是最优解在边界g(x)=0上，对应约束1) x≥−1的情况。此时不等式约束转换为等式约束，也就是在λ>0、约束起作⽤的情况下，通过求∇ॖ(१∗)+௯∇ॗ(१∗)=0，得拉格朗⽇函数h(x)最优解x=−1。

所以整合这两种情况，必须满⾜λg(x)=0
因此约束g(x)最⼩化f(x)的优化问题，可通过引⼊拉格朗⽇因⼦转化为在如下约束下，最⼩化拉格朗⽇函数h(x)，

上述约束条件称为KKT条件。
该KKT条件可扩展到多个等式约束和不等式约束的优化问题。