微信公众号：创享日记
发送：高斯牛顿
获取完整报告（含源程序代码）

---

一、问题的提出
在日常生活和科学研究中，人们经常会遇到这样一类问题：在某些条件下，寻求某一数量指标的最大或最小值。例如：在资源有限的情况下，制造尺寸最大的箱子；如何根据手中的资金情况确定收益最大的投资方向等等。这类问题用数学语言描述就是函数的最值问题，也称为最优化问题。

优化问题的一个重要应用就是数据拟合问题。数据拟合问题需要消除误差或忽略无关细节，从干扰数据中提取信号或找出趋势，将大量数据降低到可管理的数量或用简单的近似来代替复杂函数。完成这个工作的最普遍和最便于计算的方法之一就是最小二乘法。

最小二乘法是从误差拟合角度对回归模型进行参数估计或系统辨识，并在参数估计、系统辨识以及预测、预报等众多领域中得到极为广泛的应用。当我们用一个模型来描述现实中的一系列数据时，模型的预测结果与实际的测量结果总会存在一定偏差，这一偏差就称为残差。非线性最小二乘的目的就是，调整模型的参数，使得总的残差最小。常用的算法有两类，一类是搜索算法，另一类是迭代算法。本报告中采用迭代算法。

在实际生产生活中，非线性最小二乘问题的求解方法在生物、医药、电子、化学、计算机科学等领域有广泛应用。

二、问题的分析
当处理最优化问题时，若f为关于x的线性函数，通常通过对函数直接求导求得函数的全局最优解；而若f为x的非线性函数，则无法直接对函数求导以及准确求得函数的全局最优解，因此只能通过求目标函数的局部最小值，并且尝试从局部最小值拓展到全局最小值。局部最小值的求解过程中需要涉及到驻点以及目标函数的一、二阶导数，故可将该问题转化为多元函数的极值问题。

非线性最小二乘法的原理如下：
有一个未知量x∈R^n，为估计该未知量，我们进行m次观测。根据观测到的数据(t_i,y_i) (i=1,…,m)来拟合一个已知函数y=f(x,t)，其中x为待定系数，且x=(x_1,x_2,…,x_n)(n≤m)。第i次观测的理论模型可用已知函数f_i:R^n→R来描述，而第i次观测的实际值为y_i∈R，i=1,…,m。我们称
r_i (x)=r_i (x,t_i)=y_i-f_i (x,t_i)（1）
为第i次观测的残差。
给定式(1)的数学模型，在工程上，求x的估计量 的一个常用准则是最小二乘准则。该准则认为，使得所有观测的残差的平方和最小的 是最优的。
我们可以将m个残差写成向量形式
r(x)=[r_1 (x),r_2 (x),…,r_m (x)]^T（2）
此时，所有观测的残差的平方和可以写成式(3)

对于非线性最小二乘问题，一般有LM法、信赖域方法、梯度下降法、高斯牛顿法等处理方法。在本文中，主要采用高斯牛顿法研究非线性最小二乘问题。

三、高斯-牛顿算法
3.1算法的原理
高斯-牛顿算法是非线性回归模型中求回归参数进行最小二乘的一种迭代方法，其基本思想是使用泰勒级数展开式近似地代替非线性回归模型，然后通过多次迭代，多次修正回归系数，使回归系数不断逼近非线性回归模型的最佳回归系数，最后使原模型的残差平方和达到最小。其直观思想是先选取一个参数向量的参数值x，若函数f(x,t)在x_0附近有连续二阶偏导数，则在x_0的邻域内可近似地将f(x,t)看作是线性，因而可近似地用线性最小二乘法求解。
假定在第k次迭代后，将残差函数向量r(x)在x^((k))进行一阶泰勒展开，得到r(x)的线性近似

其中，∆x^((k))=(x((k))-x)为第k次迭代后的估计误差

是雅可比矩阵（Jacobian matrix）。
于是根据式(3)，最小二乘最小化的目标函数可以近似为

利用经典的线性最小二乘问题的结论，可得上式的极值点（即第(k+1)次迭代后的最优解）为


接下来再对经典的线性最小二乘问题做一个简要的介绍。线性最小二乘是一种求解线性系统参数的方法，即参数估计的方法。它的特点是需要已知参数与观察量之间的线性函数关系并且存在多余观测。
线型函数关系是指对于一个参数估计问题，我们往往不能直接获得想要的参数值，需要通过间接观测的方式去反向求解。为此，我们总是建立我们想要求解的参数X与我们易于观测量Y之间的函数关系
F(X)=Y (8)
通过已知的Y和已知的函数关系F(X)，反推出X的值。
当我们已知的这个函数关系是线性的时候，我们可以化简为
AX=Y (9)
其中A是参数X与观测Y之间的线性函数关系（线性运算（乘和加）可以由矩阵A表示）。因此，若已知观测Y和线性关系A，则可求解代求参数X。
多余观测是指除了能唯一确定某个几何或物理模型的必要观测之外的其余观测值。当存在多余观测时，无法简单对矩阵A求逆，为更加准确地求出参数X，可以借助最小二乘来求解此类问题。
解决线性最小二乘问题三种常见直接算法：正规方程、QR分解和SVD分解。一般来说，正规方程是最快的，特别是当A的条件数较小时，正规方程几乎和其他方法一样精确。SVD分解最慢，但最可靠。

3.2算法的实现
本文采用MATLAB实现高斯-牛顿算法。
依靠《随机过程》课堂中老师对MATLAB的讲解，同时借助《信号与系统》课程的实验部分学习及网上MATLAB相关教程对MATLAB算法有一定的了解。主要学习了解了本实验中会涉及的MATLAB知识，如：矩阵相关运算，系统预定义的变量eps，图形绘制功能等。
在计算机中实现高斯-牛顿算法时，我们需要给定以下输入：
①残差向量函数r ②雅可比矩阵函数J ③允许的最大迭代次数K
④能够接受的误差阈值ϵ ⑤未知参数初始值x(0)
具体算法基本步骤如下：

应用实例
实例：设一噪声模型形如y=e^(ax2+bx+c)+l，其中l为噪声，a、b、c为待解算系数。
具体代码见附录（详见报告）。
其中给定a=1,b=2,c=3；最大迭代次数K为1000；
残差函数向量为

雅可比矩阵函数为

代码运行后结果如下：

噪声模型拟合曲线如下图：

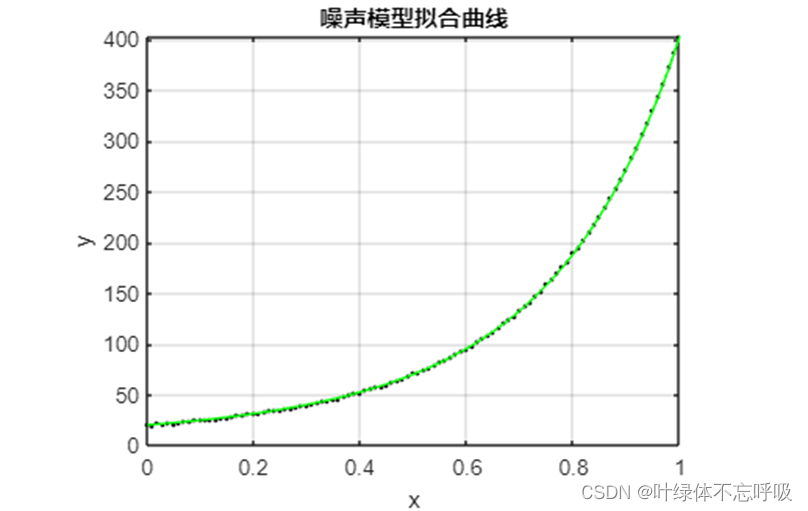
​参考文献及附录程序代码详见报告！