电磁场与电磁波实验一熟悉Matlab软件在电磁场领域的应用

前些天发现了十分不错的人工智能学习网站，通俗易懂，风趣幽默，没有广告，分享给大家，大家可以自行看看。（点击跳转人工智能学习资料）

微信公众号：创享日记
发送：matlab电磁场
获取完整无水印报告

一．实验内容
1．熟悉Matlab软件在电磁场领域的应用
2．熟悉相关代码，知道各函数的不同功能
3．运行所给代码，加深对函数功能的印象与理解

二．实验过程与结果

第1章 MATLAB在场论中的应用
1．标量函数及其可视化
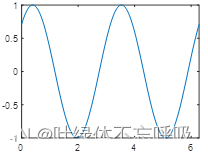
1.1使用plot函数绘制一维标量函数

x = 0:pi/1000:2*pi;         	% x取值范围由0到2π，pi/1000是递增的步长
y =sin( 2*x + pi/4);         	%表示y的函数表达式是sin类型
plot(x,y)

在这里插入图片描述

x = 0:pi/20:2*pi;    
y = sin(2*x +pi/4);   
plot(x,y,'--or')

实验结果：
在这里插入图片描述

x = 0:pi/100:2*pi;          %表示x从0到2π
y1 = sin(x);               %表示y1函数
y2 = sin(x-0.25);           %表示y2的函数
y3= sin(x-0.5);             %表示y3的函数
figure
plot(x,y1,x,y2,'--',x,y3,':')     %绘制y1,y2,y3的函数图像

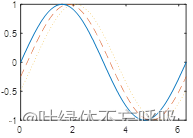
在这里插入图片描述
MATLAB中plot函数常常被用于绘制各种二维图像。利用 plot函数绘制二维点图和线图的基本格式为：plot(X,Y, LineSpec)。
其中，X由所有输入点坐标的X值组成，Y是与X对应的纵坐标所组成的向量或矩阵。若Y和X为同维向量，则以X为横坐标，Y为纵坐标绘制连线图。若X是向量，Y是行数或列数与X长度相等的矩阵，则绘制多条不同色彩的连线图，X被作为这些曲线的共同横坐标。若X和Y为同型矩阵，则以X和Y为对应元素分别绘制曲线，曲线条数等于矩阵列数。LineSpec是用户指定的绘图样式。
注意：在同时绘制多条曲线时，如果没有指定曲线属性，plot按顺序循环使用当前坐标系中颜色和线型两个属性。
1.2使用mesh函数和surf函数及相关拓展函数绘制三维曲面

 x=linspace(-2, 2, 25);     	%在-2到2取25个点
y=linspace(-2, 2, 25);      	%在-2到2取25个点
[xx, yy]=meshgrid(x, y);   	%生成网格采样点
zz=sqrt( xx.^2 + yy.^2);    	%生成矩阵Z
mesh( xx,yy,zz);         	%画出立体网状图

在这里插入图片描述

x=linspace(-2, 2, 25);     	%在-2到2取25个点
y=linspace(-2, 2, 25);      	%在-2到2取25个点
[xx, yy]=meshgrid(x, y);    	%生成网格采样点
zz=sqrt( xx.^2 + yy.^2);     	%生成矩阵Z
surf( xx,yy,zz);            	%画出着色的三维曲面

在这里插入图片描述
MATLAB中提供了mesh和surf函数来绘制三维曲面图。其中，mesh函数用于制三维的网格图，可以用三维网格图来表示绘制要求不是特别精细的三维曲面；surf函数用于绘制三维曲面图，各线条之间的面元用颜色填充。
其调用格式为：mesh(x, y,z,c)和surf(x, y, z, c)
通常情况下,x 、y ,z为维数相同的矩阵；x、y为网格坐标阵；z是网格点上的高度矩阵；c是用来定义相应点颜色等属性的数组，即由数组c指定的颜色来绘制网格图或曲面图。当c省略时，MATIAB默认c=z，即对于颜色的设定是正比于高度的,以便绘制出层次分明的三维图形。当x，y省略时,把z矩阵的列下标当作x轴坐标，把z矩阵的行下标当作y轴坐标，然后绘制三维曲面图。当x、y为向量时，要求x的长度必须等于z矩阵的列数，y的长度必须等于z矩阵的行数。
另外，MATLAB中还包含了两个和 mesh函数相似的函数﹐即带等高线的三维网格曲面函数meshc和带底座的三维网格曲面函数meshz。其用法与mesh函数相类似，区别在于meshc还在xoy平面上绘制曲面在轴方向的等高线，meshz还在xoy平面上绘制曲面的底座。同样地，surf函数也有两个类似的函数surfc和surfl，分别用于绘制具有等高线的曲面和具有光照效果的曲面。
1.3使用contour函数绘制二维和三维等高线

[X,Y]=meshgrid([-2:0.25:2]);                    	%创建X-Y网格坐标平面
Z=X.*exp(-(X.^2+Y.^2));                      	%计算函数值
contour(X,Y,Z);                               	%绘制二维等高线 
figure;     	%重建新的图形窗口
contour3(X,Y,Z,30);                            	%绘制三维等高线

在这里插入图片描述
MATLAB中的contour和contour3函数分别用于绘制标量函数的二维和三维等高线图。其基本的语法格式如下:contour(x, y,z)和contour3(x, y,z)。与mesh 函数和surf函数相同，通常情况下x、y、z为维数相同的矩阵，x、y为网格坐标阵；z是网格点上的高度矩阵。
1.4利用pcolor函数绘制伪彩色图

[X,Y]=meshgrid([0:20]);     %创建X-Y网格坐标平面
Z=sqrt(X.^2+Y.^2);         %计算函数值
figure;
hold on
pcolor(X,Y,Z);             %绘制伪彩色图
plot([0:20],[0:20],'r+');       %绘制x=y对应的点
colorbar;                  %显示色阶，默认为jet

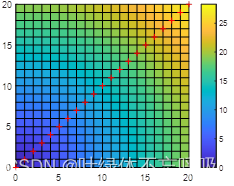
在这里插入图片描述
MATLAB中利用pcolor函数绘制伪彩色图，用于以二维平面图表现三维图形的效果，用颜色来代表三维图形的高度,其调用格式如下：
l) pcolor©
绘制指定颜色C的伪彩色图，参量C为矩阵，其元素都线性地映射于当前色图下标。2) pcolor(X,Y,C)
绘制指定颜色C和相应网格线间间距的伪彩色图，X和Y为指定网格间间距的向量或矩阵。若X、Y为矩阵，则X、Y与C维数相同；若X、Y为向量，则X的长度为矩阵C的列数，Y的长度为矩阵C的行数。
1.5利用isosurface函数绘制三维伪彩色图

[X,Y,Z]=meshgrid(linspace(-10,10));    	%形成网格数据(X,Y,Z)
V=X.^2+Y.^2-Z.^2;                  	%形成体数据V
isosurface(X,Y,Z,V,1);                	%绘制三维隐函数图形X.^2+Y.^2-Z.^2=1
axis equal
colormap([1 0 0]);                    	%改变图形颜色为红色
brighten(0.5);                        	%进行增亮  
camlight right;                       	%设置光源位置
lighting phong;                       	%设置光照模式
figure(2);
fv=isosurface(X,Y,Z,V,1);               	%计算等值面所对应的面元和顶点
p=patch(fv);                         	%绘制等值面
set(p,'FaceColor','red','EdgeColor','none');  	%修饰等值面
axis equal                            	%等比例显示

在这里插入图片描述
isosurface函数是MATLAB中用于绘制三维隐函数图形的工具。其调用格式如下： fv = isosurface(X,Y,Z, V,isovalue)；基于isovalue中指定的数值,计算体数据V并绘制等值面，即等值面连接具有指定V的点；V是关于网格数据（X,Y,Z）的体数据，isovalue是给定的等值面数值。
isosurface函数还可以得到等值面的顶点和面，然后调用patch函数直接画出来。上面语句中，fv就是函数返回的包含有顶点和面的结构。
1.6利用peaks函数演示三维曲面

[x,y,z]=peaks;               	%调用peaks函数，得到相关数据
peaks;                       %绘制peaks函数图像
axis([-inf inf -inf inf -inf inf]);

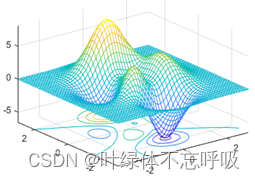
在这里插入图片描述
peaks函数，即多峰函数，可用于三维曲面的演示。在命令框中可以直接输入peaks来绘制该函数，产生一个凹凸有致的曲面，包含三个局部极大点和三个局部极小点。也可以对peaks函数取点，再以不同的方法进行绘制。
1.7采用slice函数绘制切片图

[x,y,z]=meshgrid(-2:0.2:2,-2:0.25:2,-2:0.16:2);	%产生三维立体网格
v = x.*y.*z.*exp(-(x.^2+y.^2+z.^2));	%在网格上定义函数
xslice = [-1.2:0.8:2]; yslice = 2; zslice = [-2,0];	%定义切片位置
slice(x,y,z,v,xslice,yslice,zslice)	%绘制切片图
xlabel('x'); ylabel('y'); zlabel('z');	%标注坐标轴标号
colormap hsv; 	%设置调色板为hsv

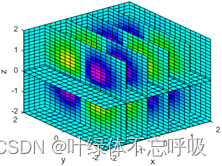
在这里插入图片描述
slice函数可用于绘制立体切片图。slice函数通过体数据来展示正交切片平面，可通过三维实体的四维切片色图来展示四维图像，用三维实体上的颜色来描述函数值的变化情况。其基本调用格式为：slice(X,Y,Z,V,XI,YI,ZI)。利用体数据V沿着由数组XI,YI,ZI定义的表面绘制切片图，V的大小决定了每一点的颜色。
1.8利用NaN函数裁剪图形

[x,y,z]=sphere(30);
z1=z;
z1(:,1:6)=NaN;                 %将大球的一部分裁掉
c1=ones(size(z1));
surf(4*x,4*y,3*z1,c1);           %绘制大球
hold on
z2=z;
c2=2*ones(size(z2));
c2(:,1:6)=3*ones(size(c2(:,1:6)));
surf(2*x,2*y,2*z2,c2);           %绘制小球
colormap([0,1,0;0.5,0,0;1,0,0]);
grid on
hold off

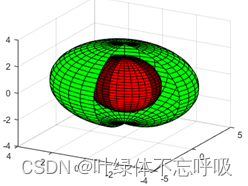
在这里插入图片描述
NaN（Not a Number）可以勇于表示不可使用的数据。利用这个特性，可将图形中需要裁减的部分对应的函数值设置为NaN，这样在绘制函数图像时，函数值为NaN对应的部分将不被显示出来，以达到裁剪的目的。
2.矢量函数及其可视化
2.1利用meshgrid函数获取采样点

x=-3:1:3; y=-2:1:2;
[X,Y]=meshgrid(x,y)

在这里插入图片描述
在利用MATLAB进行3D图形的绘制过程中，往往需要一些采样点,然后根据这些采样点来绘制出整个图形。在进行3D绘图操作时，涉及x、y、z三组数据,而x、y这两组数据可以看作在xoy平面内对坐标进行采样得到的坐标对(x,y)。meshgrid是用于生成网格采样点的函数，也称为格点矩阵。其基本格式为：[X,Y]= meshgrid(x, y)