1矢量分析

1.1 矢量代数

1.1.1 矢量加减法
1.1.2 矢量乘积
矢量的标量积：点积
矢量的矢量积：叉积
标量三重积、矢量三重积

1.2 正交坐标系

正交坐标系
正交坐标系的点积、叉积、标量三重积
度量系数
1.2.1 直角坐标系
1.2.2 圆柱坐标系
1.2.3 球坐标系

1.3 矢量微积分

1.3.1 矢量函数的积分
1.3.2 梯度、散度、旋度
标量场的梯度
矢量，大小为标量的空间最大变化率，方向为标量增加率最大的方向。

标量场的梯度与方向导数

矢量场的散度

矢量场的旋度

矢量场的散度和旋度

拉普拉斯运算符

格林恒等式
亥姆霍兹定理
如果一个矢量场的散度和旋度都已经给定，那么这个矢量场就确定了，最多附加一个常量。

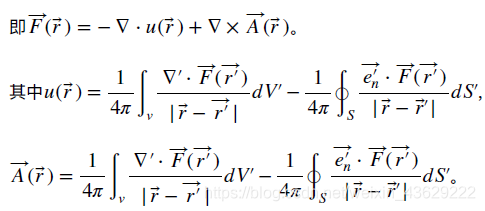
• 通量是单位时间内通过的某个曲面的量
• 散度是通量强度
• 环流量是单位时间内环绕的某个曲线的量
• 旋度是环流量强度

标量场的梯度

1、 标量场的等值面
2、 标量场梯度的定义

3、 标量场梯度的计算

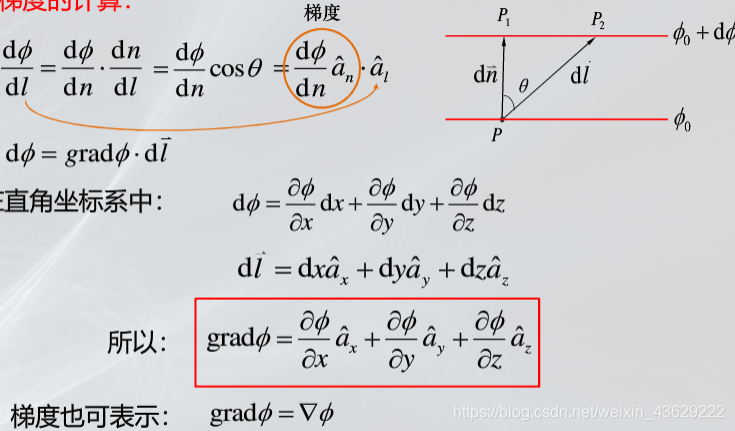
矢量场的散度

1、 矢量场的矢线（场线）
2、 矢量场的通量
3、 散度的定义
矢量场种某点的通量密度称为该点的散度。

4、 散度的计算

5、 散度定理

穿过一封闭曲面的总通量等于矢量散度的体积分。

矢量场的旋度

1、 矢量场的环量
在矢量场中，任意取一闭合曲线，将矢量沿该曲线积分称之为环量。
2、 旋度的定义
一矢量其大小等于某点最大环量密度，方向为该环的法线方向，那么该矢量称为该点矢量场的旋度。

3、 旋度的计算

4、 斯托科斯定理