函数的极限
第一步:判断极限类型
1、
常用方法:①洛必达法则 ②等价无穷小代换 ③泰勒公式
2、
常用方法:①洛必达法则
②分子分母同除以分子和分母各项中最高阶的无穷大
③基本极限:
当n=m时,极限等于
3、∞-∞ 型
常用方法:①通分化为
②根式有理化(适用于根式差)
③提无穷因子,然后等价代换或变量代换(t=
4、0 · ∞ 型
常用方法:f(x)由分子变为分母
5、
常用方法:
①凑基本极限
②改写成指数
③利用结论:
6、
这类函数一定是幂指函数,即
第二步:化简原式
a)两式相加减时考虑:
①提取极限非零的公因子
②拆开后等价无穷小代换
(拆开的条件:加法两式相除的极限≠-1,减法两式相除的极限≠1,
即若
b)看见根号相加减时,考虑有理化
c)分母为
d)幂指函数时:先改写幂指函数为指数函数,再等价代换
当
数列的极限
常见的数列极限有:
1、不定式
与函数极限方法相同,但注意不能直接使用洛必达法则,要先改写为函数极限才可以使用
2、n项和的数列极限
常用方法 ①夹逼原理 ②定积分定义 ③级数求和
当变化部分的最大值与其主体部分相比较是次量级,使用夹逼原理
(如
当变化部分的最大值与其主体部分相比较是同量级,使用定积分定义
( 如
一种常见的极限式:
3、n项连乘的数列极限
常用方法: ①夹逼原理 ②取对数化为n项和
4、递推关系
常用方法:
①当数列具有单调性时:先证明数列收敛(单调有界准则),然后令
等式
②当数列不具有单调性或单调性很难判定时:
先令
证明数列极限的“通法框架”:
(引用 来源:跌落的小刀
链接:https://www.zhihu.com/question/21068499/answer/1156867616)
一个数列极限为A在图形上(即数列的散点图)可表示为①②③三种形态,对①②③三种形态来说,均可使用夹逼定理进行计算,但是对于①②两种形态的数列来说有更为简便的证明方法,即是单调有界准则,而对于③这一种形态的数列来说只能运用夹逼定理进行证明;
- 一个问题的讨论:数列的有界性(①②③三种形态)和单调性(①②两种形态)谁依附于谁?是先证明单调性还是先证明有界性?答案是有界性。因为对于夹逼定理而言,我们需要进行放缩处理(可以结合下面的例题进行思考),而放缩的关键就是数列的有界性必须知道;对于单调有界准则而言,单调性的证明(邻项相减、相除、求导)又依赖于数列有界性;
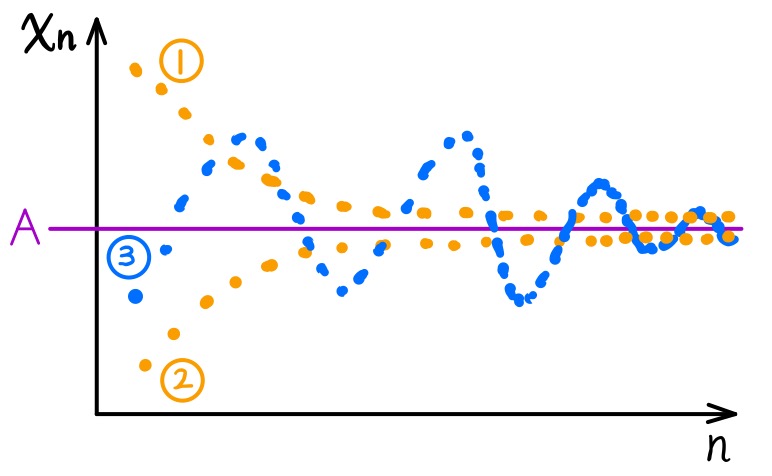
- 如何证明有界性?
我们可以看到数列的极限A在数列的有界性中扮演着重要角色,所以我们需要先求出A。这一步其实很简单,我们可以先假设数列极限存在并为A,利用已知条件解方程求出A即可,之后再证明数列极限的存在就可以了(因为我们是先假设极限存在的)。求出A之后一切就都明了了,我们可以求出数列的前几项的具体数值,然后与A进行比较,就可以知道此数列是①②③中的哪种形态了。然后所有的东西就已经陈列在我们面前:是运用夹逼还是单调有界?是单调增还是减?以及数列的界限在哪也很清楚了。然后我们就可以猜测数列的界限了,当然猜完之后我们还需要证明,也就是许多教科书上运用的归纳法,总的来说单调性的证明就是先猜后证;
- 如何证明单调性?
单调性的证明方法就是:邻项相减、相除、求导;
- 方法的选择:“单调有界准则”or“夹逼定理”?
当我们判断出所求数列属于①②③中的哪种形态时,就可以知道应该使用哪种方法了。对①②③来说均可以使用夹逼定理;对①②来说既可以使用夹逼也可以使用单调有界,但是具体哪个证明方法更简单,就因题而异了;
- 总结:数列极限证明流程
第一步:先假设极限存在并设为A,然后利用已知条件求出A(通常是解方程),继而判断出所求数列属于①②③中的哪种形态;
第二步:由第一步判断出所求数列的形态后,就可以根据数列形态猜测数列的界限了,然后运用归纳法对数列界限进行证明;
第三步:当所求数列属于①②形态时既可以运用夹逼亦可以运用单调有界准则,至于哪个更简单可以自主选择;所求数列属于③形态时,只能运用夹逼;
第四步:单调性的证明(只有数列是①②形态时才进行单调性证明),考研考的都是这种,方法是邻项相减、相除、求导;

)
)



)

)

)
)

)
)


作业 题库)

