线性DP
53. 最大子数组和
思路
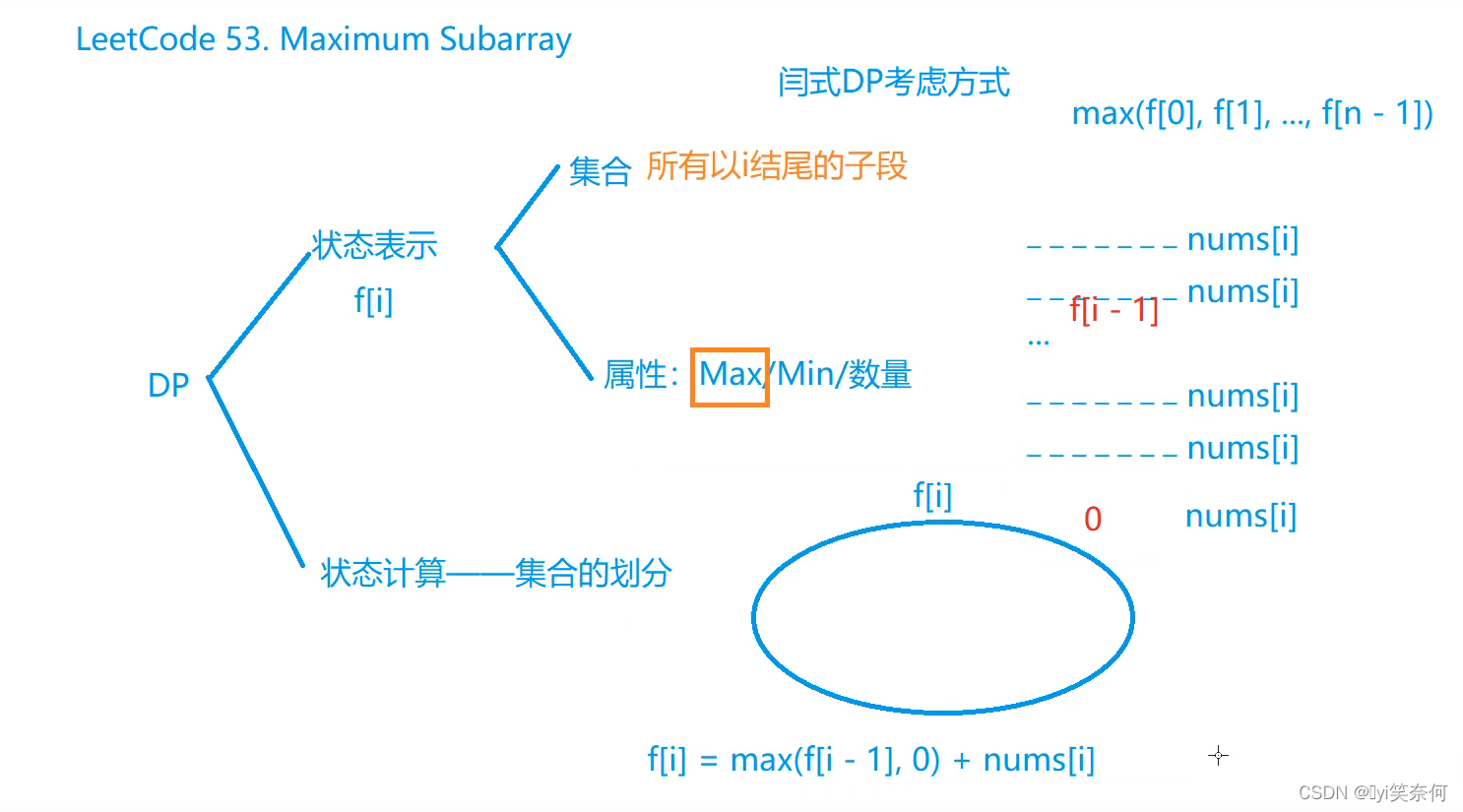
code
int maxSubArray(vector<int>& nums) {//res:最后所有状态的最终Max结果//lat:当前f[i]状态的Maxint res = INT_MIN, last = 0;for (int i = 0; i < nums.size(); i++){//当前f[i]状态最大值(使用下面的状态转移方程得出)//f[i] = max( nums[i] , f[i - 1] + nums[i] )int now = max(last, 0) + nums[i];/*最终是所有状态取一个max所以此处保存前后两个状态相互比较的最终结果*/res = max(now, res);//更新最后,当为i时候,f[i]的最大值,即lastlast = now;}return res;}120. 三角形最小路径和
思路
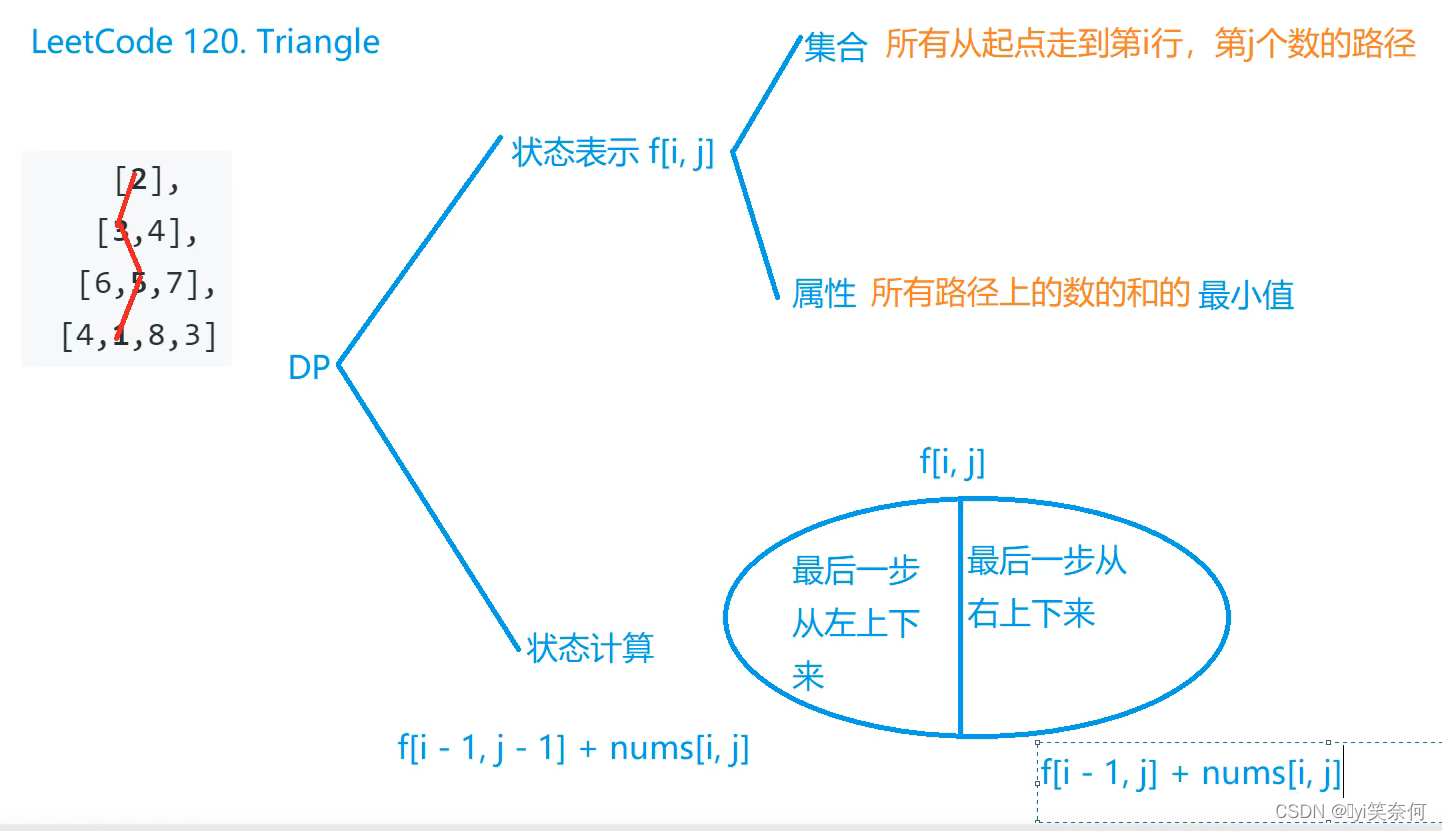
code
//自上而下
int minimumTotal(vector<vector<int>>& nums) {int n = nums.size();vector<vector<long long>>f(n, vector<long long>(n));f[0][0] = nums[0][0];for(int i = 1; i < n ;i++)for (int j = 0; j <= i; j++){f[i][j] = INT_MAX;//边界判断if (j > 0) f[i][j] = min(f[i][j], f[i - 1][j - 1] + nums[i][j]);if (j < i) f[i][j] = min(f[i][j], f[i - 1][j] + nums[i][j]);}long long res = INT_MAX;for (int i = 0; i < n; i++) res = min(res, f[n - 1][i]);return res;}//自下而上不需要考虑边界问题
int minimumTotal(vector<vector<int>>& f) {// f.size()-2 是因为最后一行不需要计算for (int i = f.size() - 2; i >= 0; i--)for (int j = 0; j <= i; j++)f[i][j] += min(f[i + 1][j], f[i + 1][j + 1]);return f[0][0];
}63. 不同路径 II
思路
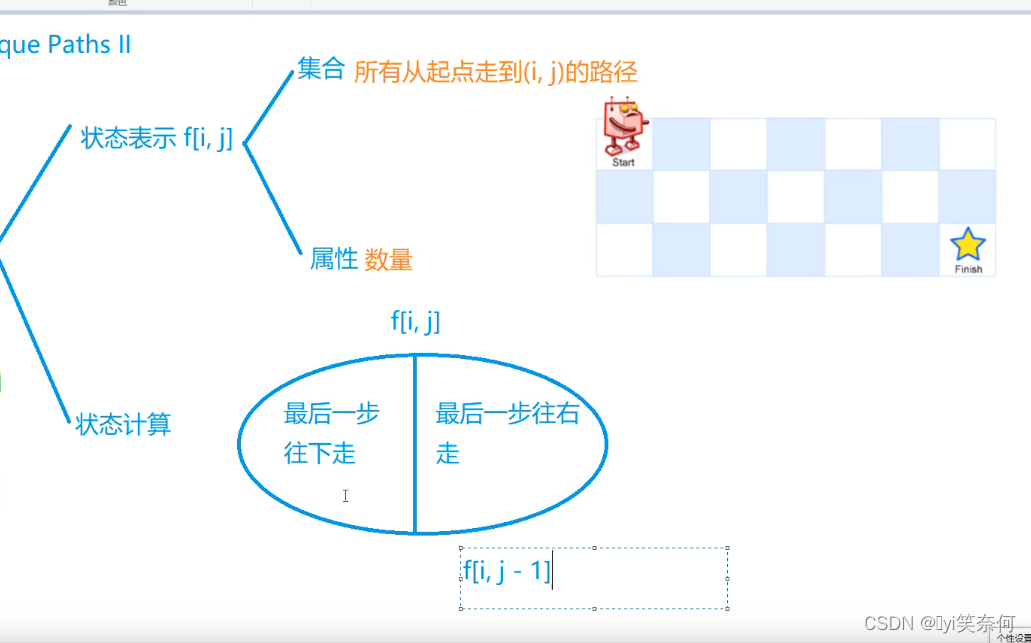
code
class Solution {
public:int uniquePathsWithObstacles(vector<vector<int>>& o) {int n = o.size();if (!n) return 0;int m = o[0].size();vector<vector<int>> f(n, vector<int>(m));for (int i = 0; i < n; i ++ )for (int j = 0; j < m; j ++ )//判断如果不为障碍物的话才执行if (!o[i][j]) {if (!i && !j) f[i][j] = 1;//特判左上角开始位置else {//如果不是第一行if (i) f[i][j] += f[i - 1][j];//如果不是第一列if (j) f[i][j] += f[i][j - 1];}}return f[n - 1][m - 1];}
};
121. 买卖股票的最佳时机
思路
此题目为一个动态规划的过程，目标是需要求得最大的利润。
1.最大利润（分析）把整个区间划分为若干份，计算出区间每一个的局部最大值，然后再比较出整体区间的最大值即为答案。
max(max[0],max[1],max[2],max[---])
2.当前最利润为：当前的元素prices[i] - 过往区间最小的值(minp)，并且更新过往最大利润res
3.最终更新最小值(minp) = min(当前最小值（即prices[i]自身）,过往区间最小值(minp))
4.总结 ：线性记录 res 和 minp 始终为过往区间的(最大利润) 与 (最小值)
code
int maxProfit(vector<int>& prices) {//res为当前最终结果int res = 0;for (int i = 0, minp = INT_MAX; i < prices.size(); i++) {//prices[i] - minp为当天最大利润//max(res, prices[i] - minp)为截止至今日，最大利润//res = max(res, prices[i] - minp);更新当前扫描的最大利润res = max(res, prices[i] - minp);//更新前面最小值(当前更新位置始终为整个区间的最小值)minp = min(minp, prices[i]);}return res;
}
