Beautiful Sequence 贪心，二进制，构造
Cyperation 模拟 ，数学
We Love Strings 分块，二进制枚举，二进制容斥dp
Writing Books 签到
根据相邻两个异或值B，因为前小于等于后，故从高到低遍历B的每一位时，第一个是1的位置，一定决定了前者与后者的大小关系。且前者这一位必定是0，后者这一位必定是1。有根据B的前缀异或和是A1^Ai,如果A1^Ai这一位是0，那么A1这一位必定填1，否则必定填0。
这样处理之后，A1会形成若干确定的填法。而对于剩余没能确定的，也就是字典序产生的由来。继续从高到低遍历每一位，当前位置i若没有确定，如果位置i之前(所有小于位置i)的有x的没有确定的，那么当前填0的贡献为(1<<x),这一贡献如果大于等于k,这一位就必定是0，否则，这一位必定是1。
#include<bits/stdc++.h>
using namespace std;
typedef long long int ll;
const int N=1e6+5;
long long n,k,b[N],T,c[N],d[50];
ll qp(ll base,ll pow)
{ll ans=1;while(pow){if(pow&1)ans=ans*base;pow>>=1;base=base*base;}return ans;
}
int main()
{cin>>T;while(T--){cin>>n>>k;int f=1;for(int i=1; i<n; i++)cin>>b[i],c[i]=c[i-1]^b[i];int t=0;memset(d,-1,sizeof(d));for(int i=1; i<n&&f; i++){for(int j=29; j>=0; j--){if(b[i]>>j) {if(d[j]!=-1&&d[j]!=1^((c[i]>>j)&1)){f=0;break;}d[j]=1^((c[i]>>j)&1);break;}}}int pre[50];memset(pre,0,sizeof(pre));pre[0]=(d[0]==-1);for(int i=1; i<=29; i++){pre[i]=pre[i-1];if(d[i]==-1)pre[i]++;}for(int i=29; i>=1; i--){if(d[i]==-1){ll temp=qp(2ll,pre[i-1]);if(k<=temp){d[i]=0;}else{d[i]=1;k-=(temp);}}}if(d[0]==-1){if(k==1){d[0]=0;}else if(k==2){d[0]=1;k=1;}}if(k>1||f==0)puts("-1");else{int p=0;for(int i=29; i>=0; i--){p=p<<1|d[i];}for(int i=0; i<n; i++){printf("%d ",(p^c[i]));}puts("");}}
}
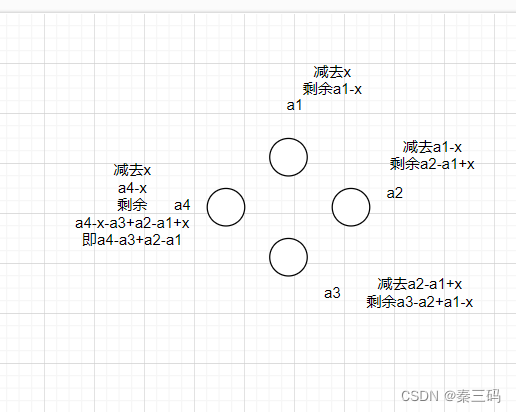
首先一个大环可以拆成若干互不影响的小环。先拆环为链，即设a1和ak共同减去了x,则接下来的删除，是固定方向的，由a1开始到ak结束。上图为偶数情况，一个合法的x，要满足每一轮相减的剩余量都大于等于0，最后的a4剩余量为0.这一过程，维护x的取值范围，判断合法即可。
对于奇数同理，只是多了一个判断剩余量是否能够整除2，和整除解出来的x是否合法。
#include<bits/stdc++.h>
using namespace std;
typedef long long int ll;
int vis[1000000+10],a[1000000+10];
int main()
{cin.tie(0);ios::sync_with_stdio(0);int t;cin>>t;while(t--){int n,k;cin>>n>>k;int zero=0;for(int i=1; i<=n; i++){cin>>a[i];if(a[i])zero=1;vis[i]=0;}if(k>n/2){if(zero){cout<<"NO"<<'\n';}elsecout<<"YES"<<'\n';continue;}int flag=1;for(int i=1; i<=n; i++){if(vis[i])continue;int now=i;ll temp=0;int op=1;ll L=-1e18,R=1e18;//cout<<" ===== "<<endl;while(!vis[now]){vis[now]=1;// cout<<now<<" ";if(op==1){R=min(R,a[now]-temp);}else{L=max(L,temp-a[now]);}op^=1;temp=a[now]-temp;now+=k;now%=n;if(now==0)now=n;}if(L>R){flag=0;break;}if(op==1){if(temp==0)continue;flag=0;}if(op==0){if(temp%2){flag=0;continue;}temp/=2;if(temp<L||temp>R){flag=0;continue;}}}if(flag==0){cout<<"NO"<<'\n';}else{cout<<"YES"<<'\n';}}return 0;
}
这题可以分块做，400给的很巧妙，这就意味这长度小于20的，可以暴力枚举，长度大于20的，不会超过20个，仍然可以暴力枚举。
对于前者，相同长度的可以暴力枚举每一位01情况，然后进行检查，一旦检查出可以的，就答案++
对于后者，也是相同长度的暴力枚举，但枚举方式变为，这x个字符串哪个参与匹配，哪个不参与。对于一个枚举出的方案，若合法(已知位置不冲突)，则这一方案的方案数为其不确定位置的个数的2次幂。但直接统计肯定会有重复。因为如2 3 4组成的集合方案数，就包含了2 3 4 5的方案数。这种重复出现在，2 3 4组成集合的问号区域，乘了2，这个2就包含了2 3 4 5的部分。故需要从2 3 4方案数里面减去。按照二进制容斥原理来说，就是满足小集合的方案数里面包含了满足大集合的，需要从小集合里面容斥掉大集合的。
#include <bits/stdc++.h>
using namespace std;
typedef long long int ll;
vector<string>v[410];
int n;
ll ans;
# define mod 998244353
void workxiao(int len)
{if(v[len].size()==0)return ;for(int i=0;i<(1<<len);i++){for(auto it:v[len]){int flag=0;for(int j=0;j<len;j++){if((i&(1<<j))){if(it[j]=='0')flag=1;}else{if(it[j]=='1')flag=1;}}if(flag==0){ans++;ans%=mod;break;}}}
}
ll dp[(1<<22)],pre[410];
void init()
{pre[0]=1;for(int i=1;i<=400;i++){pre[i]=pre[i-1]*2ll%mod;}
}
int check(string now)
{int ans=0;for(int i=0;i<now.length();i++){ans+=(now[i]=='?');}return ans;
}
void workda(int len)
{if(v[len].size()==0)return ;int nown=v[len].size();string temp="";for(int i=0;i<len;i++){temp+='?';}for(int i=1;i<(1<<nown);i++){dp[i]=0;string now=temp;int flag=0;for(int j=0;j<nown;j++){if((i&(1<<j))){for(int k=0;k<len;k++){if(v[len][j][k]!='?'){if(now[k]=='?'){now[k]=v[len][j][k];}else{if(now[k]!=v[len][j][k]){flag=1;break;}}}}}if(flag)break;}if(flag==0)dp[i]=pre[check(now)];}for(int i=1;i<(1<<nown);i++){for(int j=0;j<nown;j++){if((i&(1<<j))){dp[(i^(1<<j))]=((dp[(i^(1<<j))]-dp[i])%mod+mod)%mod;}}}for(int i=1;i<(1<<nown);i++){ans+=dp[i];ans%=mod;}}
int main()
{init();cin>>n;for(int i=1;i<=n;i++){string s;cin>>s;v[(int)(s.length())].push_back(s);}for(int i=1;i<=20;i++){workxiao(i);}for(int i=21;i<=400;i++){workda(i);}cout<<ans;return 0;
}
签到题，不赘述
