转载自 漫画:什么是二叉堆?(修正版)
什么是二叉堆?
二叉堆本质上是一种完全二叉树,它分为两个类型:
1.最大堆
2.最小堆
什么是最大堆呢?最大堆任何一个父节点的值,都大于等于它左右孩子节点的值。
什么是最小堆呢?最小堆任何一个父节点的值,都小于等于它左右孩子节点的值。
二叉堆的根节点叫做堆顶。
最大堆和最小堆的特点,决定了在最大堆的堆顶是整个堆中的最大元素;最小堆的堆顶是整个堆中的最小元素。
堆的自我调整
对于二叉堆,如下有几种操作:
插入节点
删除节点
构建二叉堆
这几种操作都是基于堆的自我调整。
下面让我们以最小堆为例,看一看二叉堆是如何进行自我调整的。
1.插入节点
二叉堆的节点插入,插入位置是完全二叉树的最后一个位置。比如我们插入一个新节点,值是 0。
这时候,我们让节点0的它的父节点5做比较,如果0小于5,则让新节点“上浮”,和父节点交换位置。
继续用节点0和父节点3做比较,如果0小于3,则让新节点继续“上浮”。
继续比较,最终让新节点0上浮到了堆顶位置。
2.删除节点
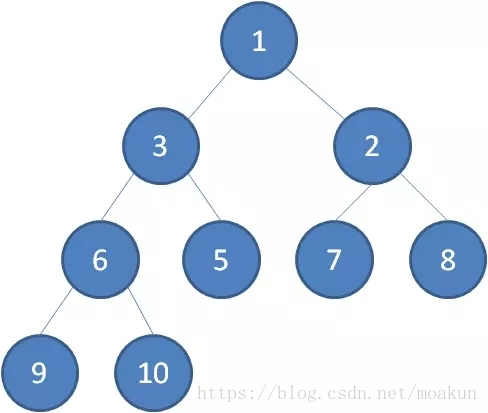
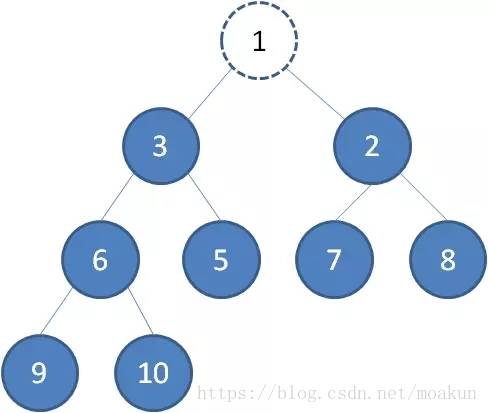
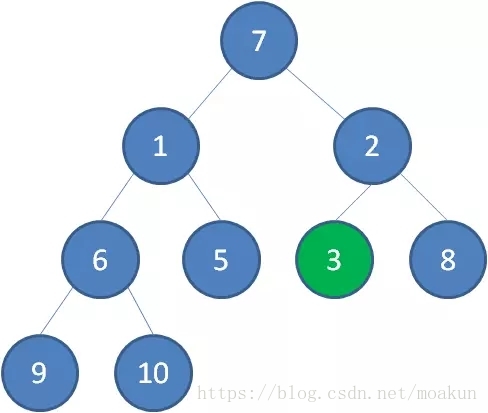
二叉堆的节点删除过程和插入过程正好相反,所删除的是处于堆顶的节点。比如我们删除最小堆的堆顶节点1。
这时候,为了维持完全二叉树的结构,我们把堆的最后一个节点10补到原本堆顶的位置。
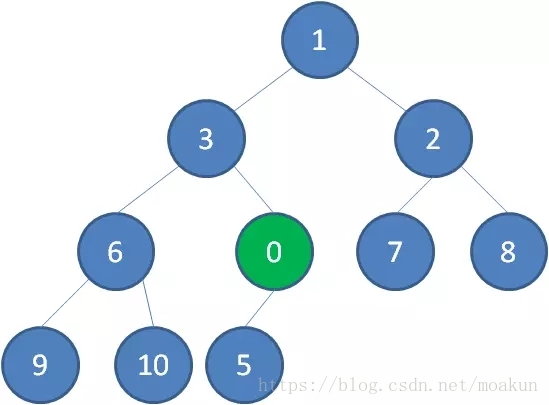
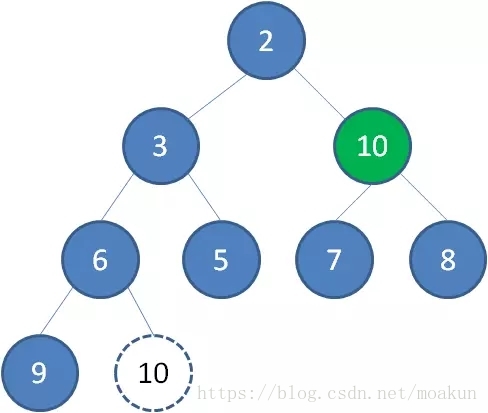
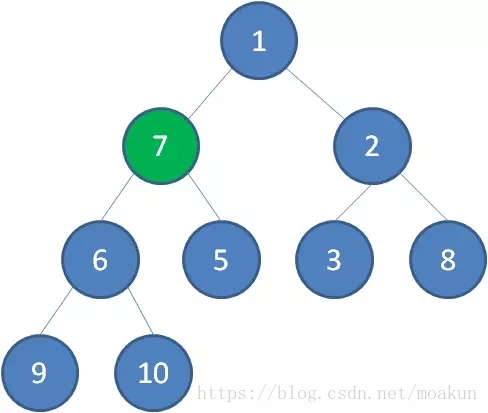
接下来我们让移动到堆顶的节点10和它的左右孩子进行比较,如果左右孩子中最小的一个(显然是节点2)比节点10小,那么让节点10“下沉”。
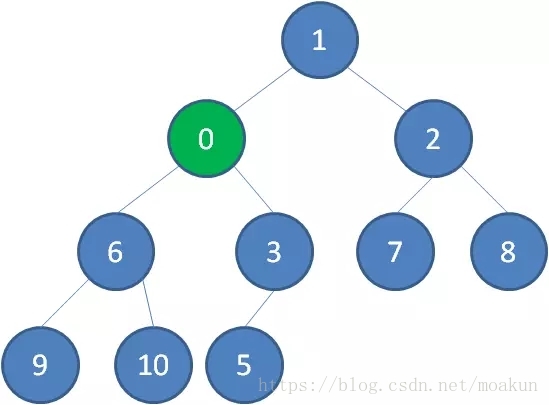
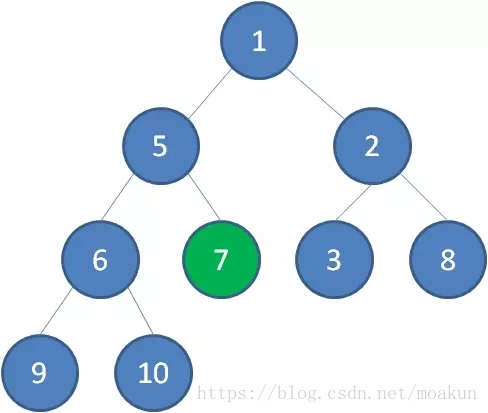
继续让节点10和它的左右孩子做比较,左右孩子中最小的是节点7,由于10大于7,让节点10继续“下沉”。
这样一来,二叉堆重新得到了调整。
3.构建二叉堆
构建二叉堆,也就是把一个无序的完全二叉树调整为二叉堆,本质上就是让所有非叶子节点依次下沉。
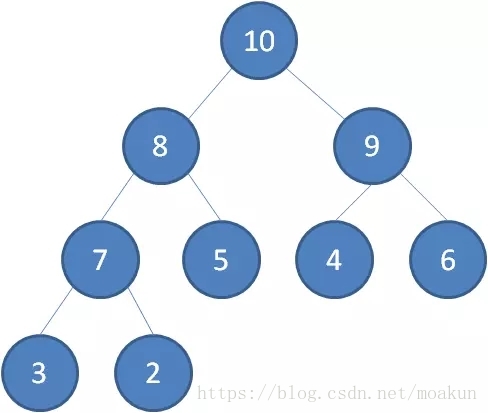
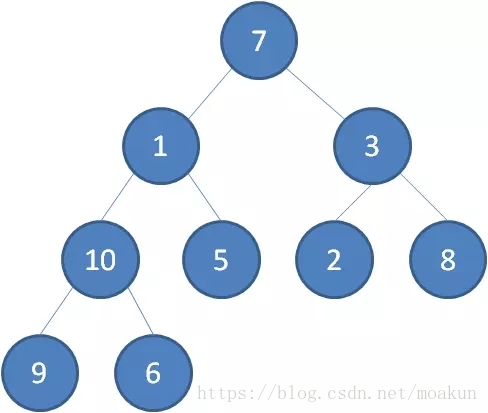
我们举一个无序完全二叉树的例子:
首先,我们从最后一个非叶子节点开始,也就是从节点10开始。如果节点10大于它左右孩子中最小的一个,则节点10下沉。
接下来轮到节点3,如果节点3大于它左右孩子中最小的一个,则节点3下沉。
接下来轮到节点1,如果节点1大于它左右孩子中最小的一个,则节点1下沉。事实上节点1小于它的左右孩子,所以不用改变。
接下来轮到节点7,如果节点7大于它左右孩子中最小的一个,则节点7下沉。
节点7继续比较,继续下沉。
这样一来,一颗无序的完全二叉树就构建成了一个最小堆。
堆的代码实现
在撸代码之前,我们还需要明确一点:
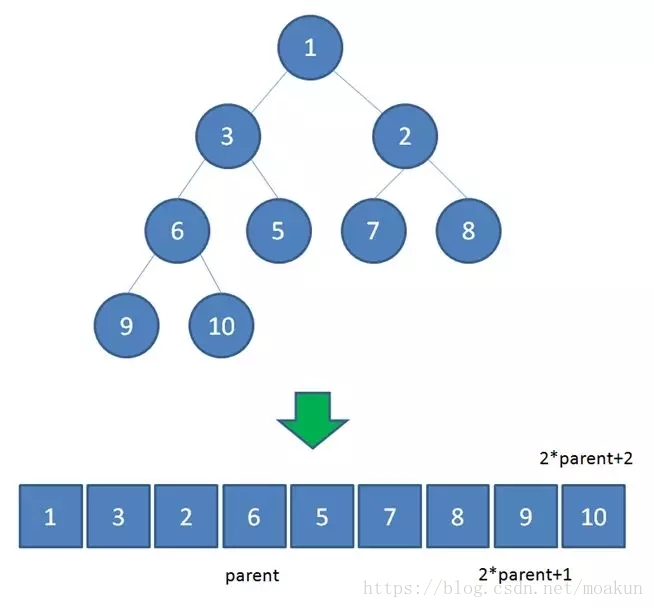
二叉堆虽然是一颗完全二叉树,但它的存储方式并不是链式存储,而是顺序存储。换句话说,二叉堆的所有节点都存储在数组当中。
数组中,在没有左右指针的情况下,如何定位到一个父节点的左孩子和右孩子呢?
像图中那样,我们可以依靠数组下标来计算。
假设父节点的下标是parent,那么它的左孩子下标就是 2*parent+1;它的右孩子下标就是 2*parent+2 。
比如上面例子中,节点6包含9和10两个孩子,节点6在数组中的下标是3,节点9在数组中的下标是7,节点10在数组中的下标是8。
7 = 3*2+1
8 = 3*2+2
刚好符合规律。
有了这个前提,下面的代码就更好理解了:
public class HeapOperator {
/**
* 上浮调整
* @param array 待调整的堆
*/public static void upAdjust(int[] array) {int childIndex = array.length-1;int parentIndex = (childIndex-1)/2;// temp保存插入的叶子节点值,用于最后的赋值int temp = array[childIndex];while (childIndex > 0 && temp < array[parentIndex]){//无需真正交换,单向赋值即可array[childIndex] = array[parentIndex];childIndex = parentIndex;parentIndex = (parentIndex-1) / 2;}array[childIndex] = temp;
}/**
* 下沉调整
* @param array 待调整的堆
* @param parentIndex 要下沉的父节点
* @param parentIndex 堆的有效大小
*/
public static void downAdjust(int[] array, int parentIndex, int length) {// temp保存父节点值,用于最后的赋值int temp = array[parentIndex];int childIndex = 2 * parentIndex + 1;while (childIndex < length) {// 如果有右孩子,且右孩子小于左孩子的值,则定位到右孩子if (childIndex + 1 < length && array[childIndex + 1] < array[childIndex]) {childIndex++;}// 如果父节点小于任何一个孩子的值,直接跳出if (temp <= array[childIndex])break;//无需真正交换,单向赋值即可array[parentIndex] = array[childIndex];parentIndex = childIndex;childIndex = 2 * childIndex + 1;}array[parentIndex] = temp;
}/**
* 构建堆
* @param array 待调整的堆
*/
public static void buildHeap(int[] array) {// 从最后一个非叶子节点开始,依次下沉调整for (int i = array.length / 2; i >= 0; i--) {downAdjust(array, i, array.length - 1);}
}public static void main(String[] args) {int[] array = new int[] {1,3,2,6,5,7,8,9,10,0};upAdjust(array);System.out.println(Arrays.toString(array));array = new int[] {7,1,3,10,5,2,8,9,6};buildHeap(array);System.out.println(Arrays.toString(array));
}
}代码中有一个优化的点,就是父节点和孩子节点做连续交换时,并不一定要真的交换,只需要先把交换一方的值存入temp变量,做单向覆盖,循环结束后,再把temp的值存入交换后的最终位置。