漫画：什么是堆排序

转载自漫画：什么是堆排序

在上一篇漫画中，小灰介绍了 二叉堆 这样一种强大的数据结构：

漫画：什么是二叉堆？（修正版）

那么，这个二叉堆怎样来使用呢？我们这一期将会详细讲述。

让我们回顾一下二叉堆和最大堆的特性：

1.二叉堆本质上是一种完全二叉树

2.最大堆的堆顶是整个堆中的最大元素

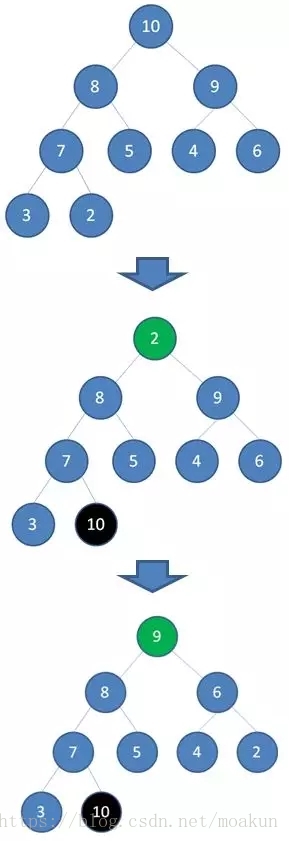
当我们删除一个最大堆的堆顶（并不是完全删除，而是替换到最后面），经过自我调节，第二大的元素就会被交换上来，成为最大堆的新堆顶。

正如上图所示，当我们删除值为10的堆顶节点，经过调节，值为9的新节点就会顶替上来；当我们删除值为9的堆顶节点，经过调节，值为8的新节点就会顶替上来.......

由于二叉堆的这个特性，我们每一次删除旧堆顶，调整后的新堆顶都是大小仅次于旧堆顶的节点。那么我们只要反复删除堆顶，反复调节二叉堆，所得到的集合就成为了一个有序集合，过程如下：

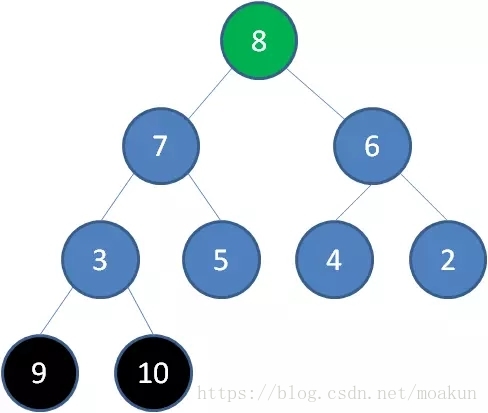
删除节点9，节点8成为新堆顶：

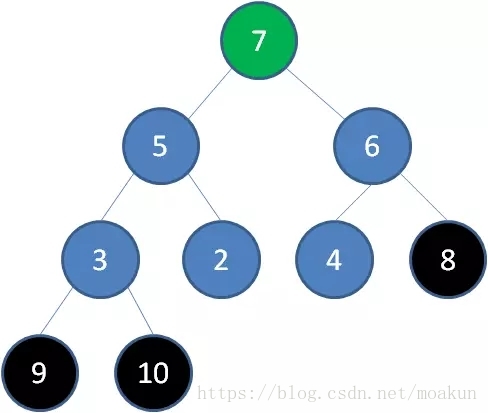
删除节点8，节点7成为新堆顶：

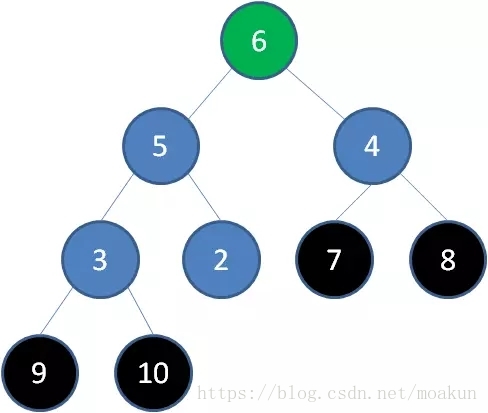
删除节点7，节点6成为新堆顶：

删除节点6，节点5成为新堆顶：

删除节点5，节点4成为新堆顶：

删除节点4，节点3成为新堆顶：

删除节点3，节点2成为新堆顶：

到此为止，我们原本的最大堆已经变成了一个从小到大的有序集合。之前说过二叉堆实际存储在数组当中，数组中的元素排列如下：

由此，我们可以归纳出堆排序算法的步骤：

1. 把无序数组构建成二叉堆。

2. 循环删除堆顶元素，移到集合尾部，调节堆产生新的堆顶。

public class HeapSort {
/**
* 下沉调整
* @param array     待调整的堆
* @param parentIndex    要下沉的父节点
* @param parentIndex    堆的有效大小
*/
public static void downAdjust(int[] array, int parentIndex, int length) {// temp保存父节点值，用于最后的赋值int temp = array[parentIndex];int childIndex = 2 * parentIndex + 1;while (childIndex < length) {// 如果有右孩子，且右孩子大于左孩子的值，则定位到右孩子if (childIndex + 1 < length && array[childIndex + 1] > array[childIndex]) {childIndex++;}// 如果父节点小于任何一个孩子的值，直接跳出if (temp >= array[childIndex])break;//无需真正交换，单向赋值即可array[parentIndex] = array[childIndex];parentIndex = childIndex;childIndex = 2 * childIndex + 1;}array[parentIndex] = temp;
}/**
* 堆排序
* @param array     待调整的堆
*/
public static void heapSort(int[] array) {// 1.把无序数组构建成二叉堆。for (int i = (array.length-2)/2; i >= 0; i--) {downAdjust(array, i, array.length);}System.out.println(Arrays.toString(array));// 2.循环删除堆顶元素，移到集合尾部，调节堆产生新的堆顶。for (int i = array.length - 1; i > 0; i--) {// 最后一个元素和第一元素进行交换int temp = array[i];array[i] = array[0];array[0] = temp;// 下沉调整最大堆downAdjust(array, 0, i);}
}public static void main(String[] args) {int[] arr = new int[] {1,3,2,6,5,7,8,9,10,0};heapSort(arr);System.out.println(Arrays.toString(arr));
}
}