MATLAB线性规划相关函数用法

一.线性规划的Matlab标准形式及软件求解

1. MATLAB中规定线性规划的标准形式为
在这里插入图片描述
其中c和 x为n 维列向量， A、 Aeq 为适当维数的矩阵，b 、beq为适当维数的列向量。（Aeq 对应约束条件中等式约束的系数矩阵，A为约不等式约束的系数矩阵）

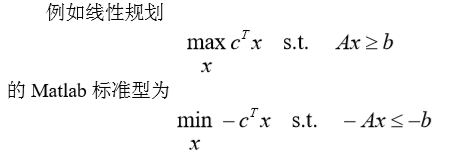
2. MATLAB函数用法——linprog

[x,fval]=linprog(c,A,b,Aeq,beq,LB,UB,OPTIONS)

这里 x返回最优值对应自变量大多数是一个向量，fval 返回目标函数的最优值，A是不等式矩阵，b不等式右边的列向量，Aeq等式约束矩阵，beq等式右边的列向量，LB 和 UB 分别是变量 x的下界和上界， OPTIONS 是控制参数。（b,beq,LB,UB均为列向量）

3.例题
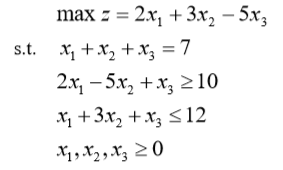
在这里插入图片描述

clc;clear;
c=[2;3;-5];
A=[-2,5,-1;1,3,1]; 
b=[-10;12]; 
Aeq=[1,1,1]; 
beq=7; 
[x,fval]=linprog(-c,A,b,Aeq,beq,zeros(3,1)); %MATLAB中所给函数求的是最小值因为题目中求最大值所以-c
fval=-fval;

4.可以转化为线性规划的问题
①对绝对值的处理
在这里插入图片描述
对于“x=u-v”和“|x|=u+v”，任何一个数都可以被两个非负数表示如果这个数为正数＋，那么x=u，v=0；如果这个数为负数－，那么x=v，u=0.
②例题

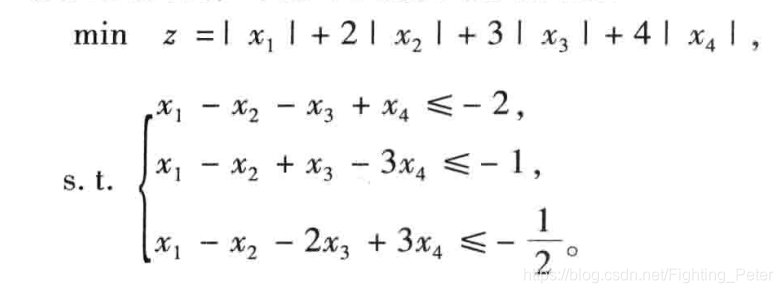
clc;clear;
c=1:4;
c=[c,c]';
A=[1 -1 -1 1;1 -1 1 -3;1 -1 -2 3];
A=[A,-A];                               %构造变换矩阵
b=[-2 -1 -0.5]';
[y,fval]=linprog(c,A,b,[],[],zeros(8,1));%没有等式约束，对应空矩阵[]
x=y(1:4)-y(5:end);                      %变回到原问题x=u-v，对于y前四个为u，后四个为v

对于这个方法我看到只能用一个字形容——妙啊

二.整数线性规划的Matlab求解

1. 线性规划中实际情况中，很多情况要求自变量为整数

在这里插入图片描述

2. 整数线性规划函数——intlinprog*

[x,fval]=intlinprog(c,intcon,A,b,Aeq,beq,LB,UB,x0,OPTIONS)

这里intcon为代表了整数决策变量所在的位置，x0为初始变量（在求之前对所求变量做一个预估）。其它和linprog函数中的含义一样。

3. 例题
在这里插入图片描述

clc;clear;
c=[-3 -2 -1]';
intcon=3;        %整数变量的位置为3 如果有3个都是整数则intcon=[1,2,3]
A=ones(1,3);
b=7;
Aeq=[4,2,1];
beq=12;
LB=zeros(3,1);
UB=[Inf;Inf;1];%对于x1,x2都是非负数，而x3为0-1之间的整数即x3=0或者1
[x,fval]=intlinprog(c,intcon,A,b,Aeq,beq,LB,UB);

3.非线性规划的Matlab标准形式及软件求解

1.MATLAB中规定非线性规划的标准形式为
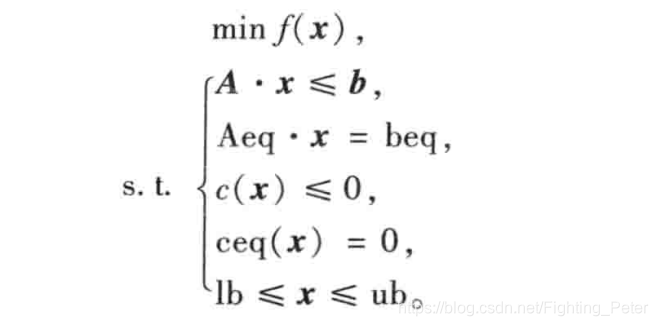
在这里插入图片描述
这里c(x)和ceq(x)为非线性向量函数

2. 非线性规划函数——fmincon

[x,fval]=fmincon(fun,x0,A,b,Aeq,beq,LB,UB,nonlcon,OPTIONS)

这里fun是用M文件定义的函数f(x)，x0是x的初始值，nonlcon是用M文件定义的非线性向量函数c(x)和ceq(x)。
其它和linprog函数中的含义一样。

3. 例题
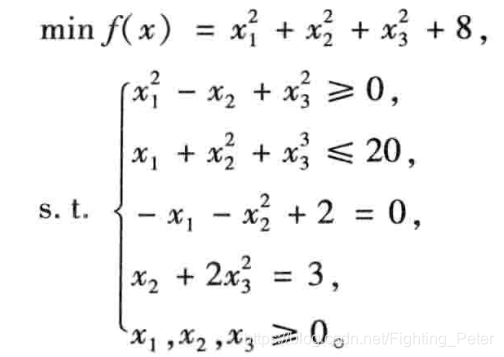
在这里插入图片描述

%% 编写函数fun
function f=fun1(x)
f=sum(x.^2)+8;
end	
%% 编写函数nonlcon
function [g,h]=fun2(x)
g=[-x(1)^2+x(2)-x(3)^2,x(1)+x(2)^2+x(3)^2-20];%非线性不等式约束
h=[-x(1)-x(2)^2+2,x(2)+2*x(3)^2-3];%非线性等式约束
end
%% 主文件程序
clc;clear;
[x,fval]=fmincon(@fun1,rand(3,1),[],[],[],[],zeros(3,1),[],@fun2);

4.二次规划的Matlab标准形式及软件求解

1. MATLAB中规定二次规划的标准形式为
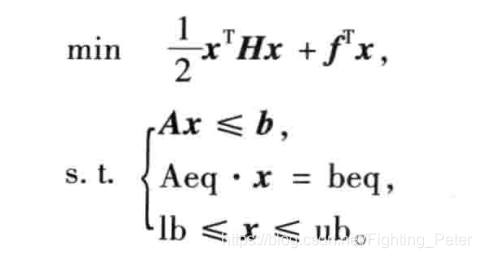
在这里插入图片描述
若某非线性规划的目标函数为自变量x的二次函数，约束条件又全是线性的，就称这种规划为二次规划

2. 二次规划函数——quadprog

[x,fval]=quadprog(H,f,A,b,Aeq,beq,LB,UB,x0,OPTIONS)

这里H为实对称矩阵，f相当于除去二次的线性规划系数

3. 例题
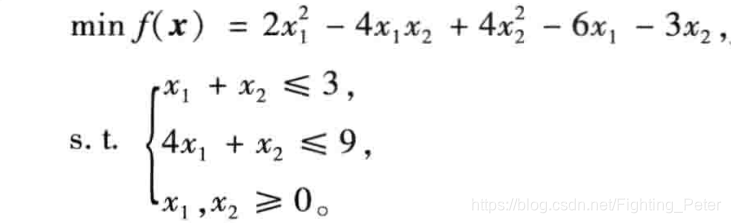
在这里插入图片描述

clc;clear;
H=[4,-4;-4,8];
f=[-6,-3]';
A=[1 1;4 1];
b=[3 9]';
[x,fval]=quadprog(H,f,A,b,[],[],zeros(2,1));%没有等式约束

5.无约束极值问题的数值解

1. fminunc和fminsearch

[x,fval] = fminunc(fun,x0,OPTIONS)

[x,fval] = fminsearch(fun,x0,OPTIONS)

使用optimset可以设置OPTIONS
fminsearch只能求出给定初值附近的一个极小值点（如果要求极大值求相反数）
2. 例题
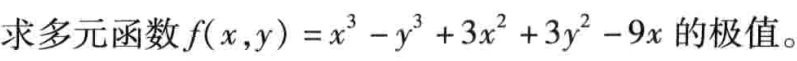
在这里插入图片描述

clc;clear;
f=@(x)x(1)^3-x(2)^3+3*x(1)^2+3*x(2)^2-9*x(1);
g=@(x)-f(x);
[x1,fval1]=fminunc(f,rand(2,1));   %求极小值
[x2,fval2]=fminsearch(g,rand(2,1));%求极大值
fval2=-fval2;

6.约束极值问题的数值解

1. 单变量非线性函数极小值——fminbnd

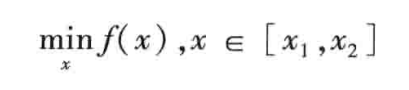
在这里插入图片描述

[x,fval]=fminbnd(fun,x1,x2,OPTIONS)

fun是用M文件定义的函数、匿名函数（@）或者Matlab中单变量数学函数。x∈[x1,x2]
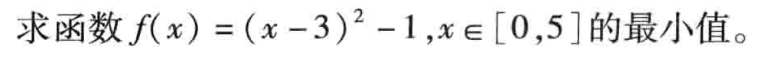
在这里插入图片描述

clc;clear;
f=@(x)(x-3)^2-1;
[f,fval]=fminbnd(f,0,5);

2.fseminf函数
在这里插入图片描述
这里c（x），ceq（x）为向量函数，Ki（x,wi）为标量函数，w1,w2,…,wn为附加变量。

[x,fval]=fseminf(fun,x0,ntheta,seminfcon,A,b,Aeq,beq,LB,UB,OPTIONS)

这里ntheta为半无穷约束Ki（x,wi）的个数，seminfcon用于定义非线性不等式约束c（x）、非线性等式约束ceq（x）和半无穷约束Ki（x,wi）的函数，seminfcon有两个输入参数x和s，s是推荐步长，也可以不使用。
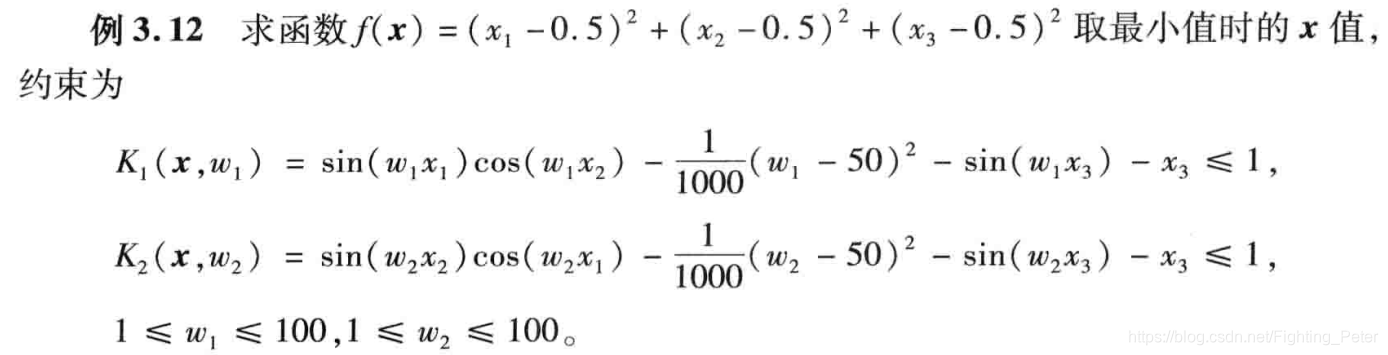
在这里插入图片描述

%% 编写fun函数文件
function f=fun1(x)
f=sum((x-0.5).^2);
end
%% 编写seminfcon函数文件
function [c,ceq,k1,k2,s]=fun2(x,s)
c=[];ceq=[];%这里没有非线性等式和不等式约束
if isnan(s(1,1))%如果s是NaN
s=[0.2,0;0.2,0];
end
%取样值
w1=1:s(1,1):100;
w2=1:s(2,1):100;
%半无穷约束
k1=sin(w1*x(1)).*cos(w1*x(2))-1/1000*(w1-50).^2-sin(w1*x(3))-x(3)-1;
k2=sin(w2*x(2)).*cos(w2*x(1))-1/1000*(w2-50).^2-sin(w2*x(3))-x(3)-1;
%画图
plot(w1,k1,'-',w2,k2,'+');
end
%% 编写主程序
clc;clear;
x0=[0.5;0.2;0.3];%如果初值不合适可能得不到可行解
[x,feval]=fseminf(@fun1,x0,2,@fun2);

3. fminimax函数
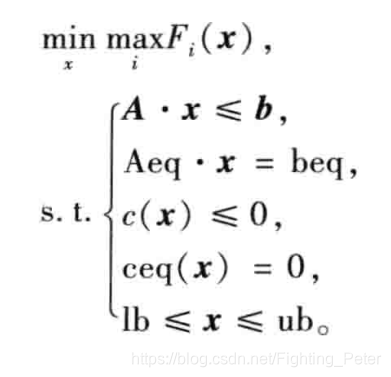
在这里插入图片描述

[x,fval]=fminimax(fun,x0,A,b,Aeq,beq,LB,UB,nonlcon,OPTIONS)

这里nonlcon是用M文件定义的非线性向量函数c(x)和ceq(x)。
在这里插入图片描述

%% 编写函数文件
function f=fun(x)
f=[2*x(1)^2+x(2)^2-48*x(1)-40*x(2)+304,-x(1)^2-3*x(2)^2,x(1)+3*x(2)-18,-x(1)-x(2),x(1)+x(2)-8];
end
%% 编写主程序调用函数文件
clc;clear;
[x,fval]=fminimax(@fun,rand(2,1));