简要

数位dp，天下第一

最重要的应该有两个：
1.状态转移式的确定
2.试填法不断往后模拟
（至今是唯一一道数位dp，究竟重要的是啥我其实也没有太多经验 ）
半年之后的UPD：为什么要试填法啊！！记搜天下第一！
至少这道题提供了很好的方法与套路

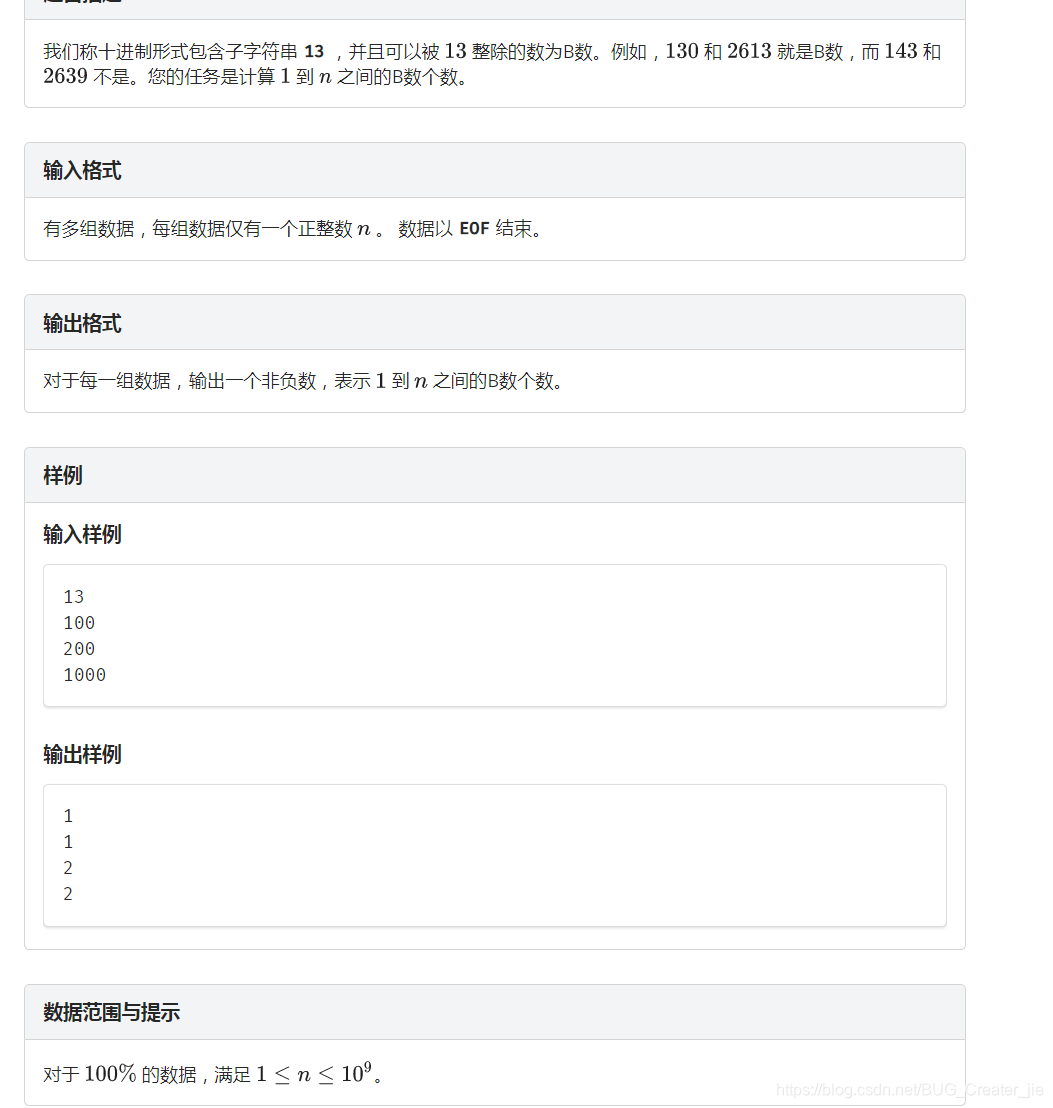
题目描述

解析

dp定义:

pos：表示位数
res：表示膜13的余数
op：表示关于出现13的状态，其中：

op=0： 啥也没有
op=1：没有出现13但最高位是3（再来个1就ok啦！）
op=2：已经存在13了

dp[pos][res][op]就是表示符合上述状态的数的数量
具体状态转移见代码

试填法

比当前最高位（设为s）小的后面可以随便填
若本位填了s就不断向后模拟，注意op（这里op=1的定义是最后一位是1）和res随着填数的转移
大于s自然不能填啦
注意：这么填最后会填到n-1，所以要么一开始就把n+1，要么特判一下n

代码

（数位dp法）

#include<bits/stdc++.h>
#define ll long long
#define mem(a,b) memset(a,b,sizeof(a))
using namespace std;
const int N=2e6+100;
const int M=2e6+100;
int dp[12][15][5],mi[15];
int a,m;
void Dp(){//预处理dpmi[0]=1;for(int i=1;i<=9;i++) mi[i]=mi[i-1]*10;dp[0][0][0]=1;for(int pos=1;pos<=10;pos++){//从后往前填 for(int i=0;i<=9;i++){for(int res1=0;res1<=12;res1++){int res2=(res1+13-i*mi[pos-1]%13)%13;if(i!=1&&i!=3) dp[pos][res1][0]+=dp[pos-1][res2][1];if(i!=3) dp[pos][res1][0]+=dp[pos-1][res2][0];if(i==3){dp[pos][res1][1]+=dp[pos-1][res2][0]+dp[pos-1][res2][1];}if(i==1) dp[pos][res1][2]+=dp[pos-1][res2][1];dp[pos][res1][2]+=dp[pos-1][res2][2];}}}
}
int solve(int n){//试填法int op=0,res1=0,ans=0;for(int pos=10;pos>=1;pos--){//从前往后填 int s=n/mi[pos-1];for(int i=s-1;i>=0;i--){//s以下自由填 int op2,resnow=(res1+i*mi[pos-1])%13,res2=(13-resnow)%13;//res2是后面需要的模数if(op==2||(op==1&&i==3)) op2=2;else if(i==1) op2=1;else op2=0;ans+=dp[pos-1][res2][2];if(op2) ans+=dp[pos-1][res2][1];if(op2==2) ans+=dp[pos-1][res2][0]; }if(op!=2){if(op==1&&s==3) op=2;else if(s==1) op=1;else op=0;}res1=(res1+s*mi[pos-1])%13;n%=mi[pos-1];} 
//	if(op==2&&res1==0) ans++;
//这里的特判和下面的a+1有一个即可return ans;
}
int main(){Dp();while(scanf("%d",&a)!=EOF){printf("%d\n",solve(a+1));}return 0;
}
/*
13
100
200
1000
*/

thanks for reading！