[2021-07-19 内测] NOIP
- 操作
- description
- solution
- code
- 异或
- description
- solution
- code
- 等级
- description
- solution
- code
- 矩阵
- description
- solution
- code
操作
description
有n堆石子,每堆石子都有一定的数量,第i堆石子的数量用Ai表示。
任意两堆石子均可合并,一堆石子也可 以分成两堆非空的石子。
一次合并或一次分裂都算一次操作。
经过若干次操作以后,石子还剩m堆,告诉你m堆石子的数量Bi,问至少经历了几次操作。
Input
多组数据,第一行一个正整数T表示数据组数,对于每组数据:
第一行,首先一个数n,接下来是n个正整数表示A1~An。
第二行,首先一个数m,接下来是m个正整数表示B1~Bm。
保证A数组的和等于B数组的和。
Output
每组数据一个整数,表示至少经历了多少次操作,保证答案在int范围之内。
Example
standard input
1
1 6
3 1 2 3
standard output
2
Note
对于100%的数据,1 ≤ n,m ≤ 10,1 ≤ Ai,Bi ≤ 50,1 ≤ T ≤ 5
solution
法一:搜索加剪枝,上限是O(nn)O(n^n)O(nn),但肯定跑不满

法二:状压DPDPDP
合并某些AAA中的数,然后再拆成BBB中的某些数
可以把这样的操作看成合并某些AAA中的数和某些BBB中的数,使之和相等即可
显然,最坏的操作上界是A,BA,BA,B都合成只剩一个数,n−1+m−1=n+m−2n-1+m-1=n+m-2n−1+m−1=n+m−2次操作
但是每当有一段AAA的合成数和BBB的一段合成数相同时,A,BA,BA,B就可以不再跟其它的数合并
A,BA,BA,B的操作数都减少111,一共减少了222次总操作数
也就是说,一段和相同,就会减少222次操作,而我们则想要和相同的段数越多越好
可以把BBB中的数取反合在AAA后面,和相同也就变成了求和等于000
设fi:f_i:fi: 操作了iii集合的数的最多段数,sumi:sum_i:sumi: 选的iii集合的数的和,如果为000,那么fif_ifi则+1+1+1
最后的f(1<<(n+m)−1)f_{(1<<(n+m)-1)}f(1<<(n+m)−1)肯定会+1+1+1,但是这个多余贡献是不会减少总操作数的
code
#include <cstdio>
#include <iostream>
using namespace std;
int T, n, m;
int A[25], f[1 << 20], sum[1 << 20];int lowbit( int x ) {return x & ( -x );
}int main() {scanf( "%d", &T );while( T -- ) {scanf( "%d", &n );for( int i = 1;i <= n;i ++ )scanf( "%d", &A[i] );scanf( "%d", &m );for( int i = 1;i <= m;i ++ )scanf( "%d", &A[i + n] ), A[i + n] = - A[i + n];n += m, m = 1 << n, f[0] = 0;for( int i = 1;i < m;i ++ ) {sum[i] = 0, f[i] = 0;for( int j = 1;j <= n;j ++ )if( 1 << j - 1 & i ) {sum[i] = sum[i ^ ( 1 << j - 1 )] + A[j];f[i] = max( f[i ^ ( 1 << j - 1 )] + ( sum[i] == 0 ), f[i] );}}printf( "%d\n", n - 2 - ( f[m - 1] - 1 << 1 ) );}return 0;
}
异或
description
N 个数字,要求选择 M 次,每次从 N 个数中选出两个数(Ai,Aj)(但不能和之前某次选择 相同)
此次选择的得分为 Ai xor Aj。 求最大得分。
Input
第一行包含两个整数 N,M 接下来一行共 N 个整数描述 N 个数字。
Output
输出一个整数,表示最大得分除以 10^9+7 的余数
Example
Standard input
3 2
1 2 3
Standard output
5
Note
对于 100%的测试数据,N≤50000,0≤Ai≤10^9
solution
-
二分第MMM大的值xxx,
check异或和大于等于xxx的个数-
建字典树,每个点记录经过其的个数cntcntcnt
-
对每个aia_iai进行字典树查找,显然想要大于等于xxx就尽可能异或出现111
aia_iai的jjj位为1(0)1(0)1(0),那么就去字典树nownownow的0(1)0(1)0(1)端的点找
- 如果存在,必定会出现1<<j1<<j1<<j的贡献,加上之前路径上的贡献(记为sumsumsum)
- 如果已经大于等于xxx,则直接加上该点的cntcntcnt,不用继续往下搜了
- 如果还不够,sumsumsum累加该位贡献,继续下一位的搜索
- 如果不存在,那么就只能放弃jjj位的贡献
- 如果现在的sumsumsum加上假设后面位全为111的贡献和(1<<j)−1(1<<j)-1(1<<j)−1都不够,也不用搜了(不可能)
- 否则,还是继续下一位的搜索
- 如果存在,必定会出现1<<j1<<j1<<j的贡献,加上之前路径上的贡献(记为sumsumsum)
-
为了卡常不TTT,字典树应只建一次在二分外面,那么就会造成统计大于等于xxx的异或个数时(x,y),(y,x)(x,y),(y,x)(x,y),(y,x)都被计算进入,所以真正的个数应该是要除以222的
-
-
然后我们就确定了第MMM大的值xxx
大于等于xxx的个数可能多于MMM个,最后的答案会涉及减去多余个数乘xxx的贡献
多余个数的值一定是xxx,不然第MMM大就不可能是xxx
第MMM大是xxx,意味着大于等于x+1x+1x+1的异或组合小于MMM个
-
最后就只剩下求值的问题了
-
枚举aia_iai,边重构字典树边计算答案值和真正的个数,这样就不需要除以222了
-
走法与上面同理
-
怎么在计算cntcntcnt的同时计算ansansans,在确定不用继续往下搜的情况那里统计即可
字典树重构时,开一个数组onei:one_i:onei: 经过该点的第iii位为111的个数
统计时,枚举位jjj,如果位jjj要产生1<<j1<<j1<<j的贡献,显然数要与aia_iai的jjj位不同才行
- aia_iai的jjj位为111,则应该为cnt−onejcnt-one_jcnt−onej的个数
- aia_iai的jjj位为000,则就是onejone_jonej的个数
-
code
#include <cstdio>
#include <iostream>
using namespace std;
#define mod 1000000007
#define maxn 50005
struct node {int cnt;int son[2], one[30];
}t[maxn * 29];
int n, m, tot, mid;
long long cnt, ans;
int digit[30], a[maxn];void read( int &x ) {x = 0; char s = getchar();while( s < '0' || s > '9' ) s = getchar();while( '0' <= s && s <= '9' ) {x = ( x << 1 ) + ( x << 3 ) + ( s ^ 48 );s = getchar();}
}long long dfs_cnt( int now, int d, int sum, int x ) {if( d < 0 ) return 0;long long num = 0;int k = x >> d & 1;if( t[now].son[k ^ 1] ) {if( sum + ( 1 << d ) >= mid ) num += t[t[now].son[k ^ 1]].cnt;else num += dfs_cnt( t[now].son[k ^ 1], d - 1, sum + ( 1 << d ), x );}if( t[now].son[k] && sum + ( 1 << d ) - 1 >= mid ) num += dfs_cnt( t[now].son[k], d - 1, sum, x );return num;
}long long calc() {long long num = 0;for( int i = 1;i <= n;i ++ )num += dfs_cnt( 0, 29, 0, a[i] );return ( num >> 1 );
}void add( int now, int x ) {for( int i = 29;~ i;i -- ) {int k = ( x >> i & 1 ) ^ 1;if( k ) ans = ( ans + ( 1ll << i ) * t[now].one[i] ) % mod;else ans = ( ans + ( 1ll << i ) * ( t[now].cnt - t[now].one[i] ) ) % mod;}
}long long dfs_sum( int now, int d, int sum, int x ) {if( d < 0 ) return 0;long long num = 0;int k = x >> d & 1;if( t[now].son[k ^ 1] ) {if( sum + ( 1 << d ) >= mid ) add( t[now].son[k ^ 1], x ), num += t[t[now].son[k ^ 1]].cnt;else num += dfs_sum( t[now].son[k ^ 1], d - 1, sum + ( 1 << d ), x );}if( t[now].son[k] && sum + ( 1 << d ) - 1 >= mid ) num += dfs_sum( t[now].son[k], d - 1, sum, x );return num;
}void solve() {for( int i = 0;i <= tot;i ++ )t[i].cnt = t[i].son[0] = t[i].son[1] = 0;tot = 0;for( int i = 1;i <= n;i ++ ) {int len = 0;for( int j = 29;~ j;j -- )if( a[i] >> j & 1 ) digit[++ len] = j;int now = 0;for( int j = 29;~ j;j -- ) {int c = a[i] >> j & 1;if( ! t[now].son[c] ) t[now].son[c] = ++ tot;now = t[now].son[c];t[now].cnt ++;for( int k = 1;k <= len;k ++ )t[now].one[digit[k]] ++;}cnt += dfs_sum( 0, 29, 0, a[i] );}
}int main() {read( n ), read( m );for( int i = 1;i <= n;i ++ ) {read( a[i] );int now = 0;for( int j = 29;~ j;j -- ) {int c = a[i] >> j & 1;if( ! t[now].son[c] ) t[now].son[c] = ++ tot;now = t[now].son[c];t[now].cnt ++;}}int l = 1, r = ( 1 << 30 ) - 1, val = 1;while( l <= r ) {mid = ( l + r ) >> 1;if( calc() >= m ) val = mid, l = mid + 1;else r = mid - 1;}mid = val;solve();printf( "%lld\n", ( ans - 1ll * val * max( 0ll, cnt - m ) % mod + mod ) % mod );return 0;
}
等级
description
数组A中有n个数,下标从1开始。
如果数组中某一段满足其中的所有元素可以组成一个公差为k的等差数 列,则这一段具备k的等级。
需要注意的是,一个数可以算作公差为任意整数的等差数列。
现在有m个操作,分为两类:
1 X Y: 表示X位置的数变成Y
2 L R K: 表示查询[L,R]是否 等级为k。
Input
第一行两个正整数n,m。 第二行n个非负整数Ai。 接下来m行每一行表示一个操作,格式上文已给出。
强制在线:在本题中x,y,l,r都是经过加密的,需要异或你之前输出的Yes的个数来进行解密。
由于输入量较大,建议使用快读。
Output
对于每个操作2,输出一行,”Yes”表示可以达到等级K,”No”表示不可以。
Example
standard input
5 3
1 3 2 5 6
2 1 5 1
1 5 4
2 1 5 1
standard output
No
Yes
Note
对于100%的数据,1 ≤ n,m ≤ 300000,0 ≤ Ai,y ≤ 10^9,1 ≤ l ≤ r ≤ n,1 ≤ x ≤ n,0 ≤ k ≤ 10^9
solution
法一:长达7k7k7k的无脑码农题
- 线段树维护区间最大值
- 线段树维护区间最小值
- 线段树维护区间是否重复——
set/map离散化 - 线段树维护区间差的gcdgcdgcd
- 如果是等差数列公差为kkk,必然满足
- 最大值−-−最小值=(r−l)∗k=(r-l)*k=(r−l)∗k
- 区间无重复
- gcd=kgcd=kgcd=k

法二:数学真是太强了!
既然是等差数列,则必定满足等差数列的一次方和,二次方和.........高次方和的多个公式
显然可以线段树维护区间的一次方和,二次方和.........
判断是否跟公式一一符合即可
至于能否被卡,显然是次方维护越多就越难被卡掉
窃以为到三次方就唯一确定是否是等差数列了
不过本题只用维护到平方和即可
具体公式推导可详见博主置顶数学公式证明博文,Thanks♪(・ω・)ノ
code
#include <cstdio>
#include <iostream>
using namespace std;
#define inf 0x7f7f7f7f
#define int long long
#define maxn 300005
struct node {int Min, Max, sum1, sum2;
}t[maxn << 2];
int n, m;
int a[maxn];void read( int &x ) {x = 0; char s = getchar();while( s < '0' || s > '9' ) s = getchar();while( '0' <= s && s <= '9' ) {x = ( x << 1 ) + ( x << 3 ) + ( s ^ 48 );s = getchar();}
}void merge( node &t, node x, node y ) {t.Max = max( x.Max, y.Max );t.Min = min( x.Min, y.Min );t.sum1 = x.sum1 + y.sum1;t.sum2 = x.sum2 + y.sum2;
}void build( int num, int l, int r ) {if( l == r ) {t[num].Max = t[num].Min = t[num].sum1 = a[l];t[num].sum2 = a[l] * a[l];return;}int mid = ( l + r ) >> 1;build( num << 1, l, mid );build( num << 1 | 1, mid + 1, r );merge( t[num], t[num << 1], t[num << 1 | 1] );
}void modify( int num, int l, int r, int pos ) {if( l == r ) {t[num].Max = t[num].Min = t[num].sum1 = a[l];t[num].sum2 = a[l] * a[l];return;}int mid = ( l + r ) >> 1;if( pos <= mid ) modify( num << 1, l, mid, pos );else modify( num << 1 | 1, mid + 1, r, pos );merge( t[num], t[num << 1], t[num << 1 | 1] );
}node query( int num, int l, int r, int L, int R ) {if( L <= l && r <= R ) return t[num];int mid = ( l + r ) >> 1;node ans = { inf, -inf, 0, 0 };if( L <= mid ) merge( ans, ans, query( num << 1, l, mid, L, R ) );if( mid < R ) merge( ans, ans, query( num << 1 | 1, mid + 1, r, L, R ) );return ans;
}signed main() {scanf( "%lld %lld", &n, &m );for( int i = 1;i <= n;i ++ )scanf( "%lld", &a[i] );build( 1, 1, n );int opt, x, y, l, r, k, cnt = 0;while( m -- ) {scanf( "%lld", &opt );if( opt & 1 ) {scanf( "%lld %lld", &x, &y );x ^= cnt, y ^= cnt;if( a[x] == y ) continue;else a[x] = y; modify( 1, 1, n, x );}else {scanf( "%lld %lld %lld", &l, &r, &k );l ^= cnt, r ^= cnt;node MS = query( 1, 1, n, l, r );if( MS.Max - MS.Min != ( r - l ) * k ) {printf( "No\n" );continue;}int N = r - l + 1, a = MS.Min;if( N * a + N * ( N - 1 ) / 2 * k != MS.sum1 ) {printf( "No\n" );continue;}if( N * a * a + N * ( N - 1 ) * k * a + ( N - 1 ) * N * ( 2 * N - 1 ) / 6 * k * k != MS.sum2 ) {printf( "No\n" );continue;}cnt ++;printf( "Yes\n" );}}return 0;
}
矩阵
description
有一个n∗nn*nn∗n的01矩阵,当它每一行、每一列都恰好有两个位置是1的时候,称为配对矩阵
请问从1∗11*11∗1到n∗nn*nn∗n的所有01矩阵中有多少矩阵为配对矩阵。
设 f[i]表示边长为i的配对矩阵的个数,即询问:∑i=1nfi\sum_{i=1}^nf_i∑i=1nfi
Input
第一行一个正整数n。
Output
一行一个整数表示所求答案模上998244353的值。
Example
standard input
2
standard output
1
样例解释:唯一的矩阵是 n=2,所有位置都是1的矩阵。
Note
对于100%的数据,1 ≤ n ≤ 10^7
solution
法一:王者打表前七个,找规律猜出DPDPDP转移方程

法二:正常人的推理
转换题意为:
- 有1×n1\times n1×n的序列 →\rightarrow→ 一共有nnn列
- 一共nnn次操作 →\rightarrow→ nnn行
- 第iii次选两个格子进行操作+1→+1\rightarrow+1→ 第iii行选择两个111的列位置
- 每一列111的位置 →\rightarrow→ 两次顺序操作i,ji,ji,j选择了该位置
- 最后使得每个格子的数都恰好是222
也就是说,如果第iii次操作选择了j,kj,kj,k意味着第iii行的j,kj,kj,k列为111,第j,kj,kj,k列的其中有个111是在iii行
fif_ifi定义不变,gi:g_i:gi: 长度序列为iii已经进行了一次操作(已经有两个位置为111,剩下i−1i-1i−1次操作)的方案数
-
fif_ifi的转移
-
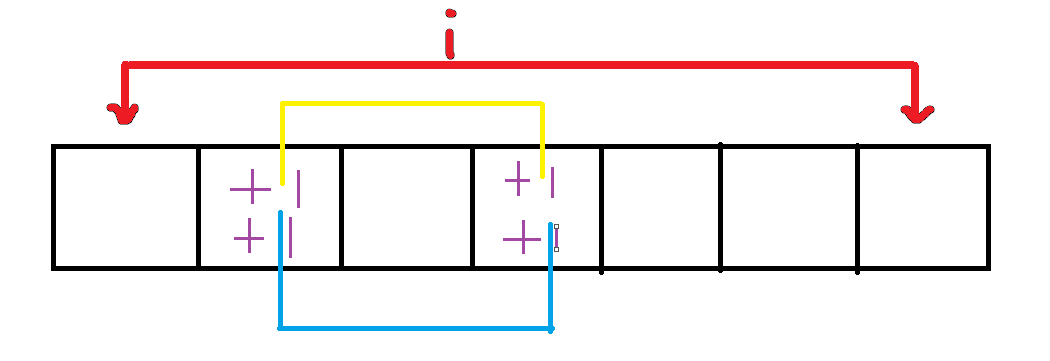
fi−2×(i−1)×Ci2f_{i-2}\times(i-1)\times C_i^2fi−2×(i−1)×Ci2,两次操作都选择同样的两个格子
- 那么两次操作顺序不会造成影响,是等价的,所以是在iii次操作中任选两次操作Ci2C_i^2Ci2
- 剩下i−2i-2i−2长度的空序列fi−2f_{i-2}fi−2
- 考虑新增行的位置(随便考虑一个位置固定也行)是一定要填的,剩下的有Ci−1i=(i−1)C_{i-1}^i=(i-1)Ci−1i=(i−1)种选择
-
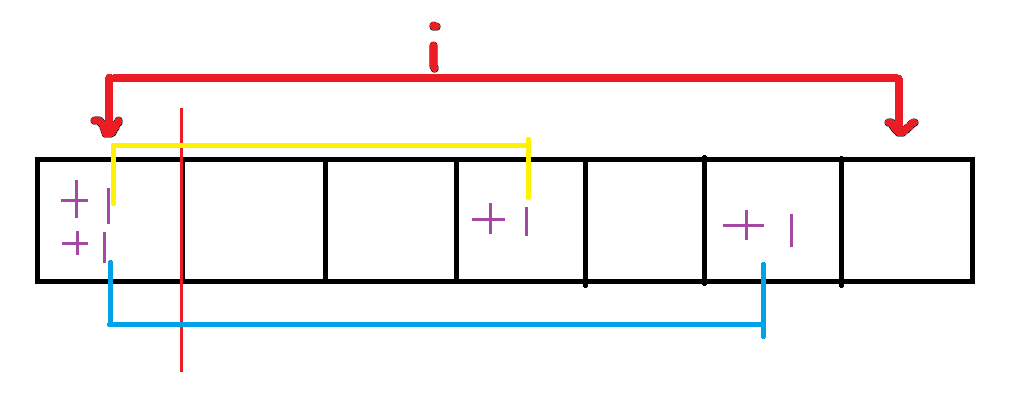
gi−1×Ci−12×Ai2g_{i-1}\times C_{i-1}^2\times A_{i}^2gi−1×Ci−12×Ai2,两次操作格子不同
-
剩下i−1i-1i−1长度序列且有两个已经为111,gi−1g_{i-1}gi−1
-
与固定新增块相连的两个块随便选,Ci−12C_{i-1}^2Ci−12
-
在iii次操作中选两次操作,操作顺序不同,是不等价的,Ai2A_{i}^2Ai2
-
-
-
gig_igi的转移
-
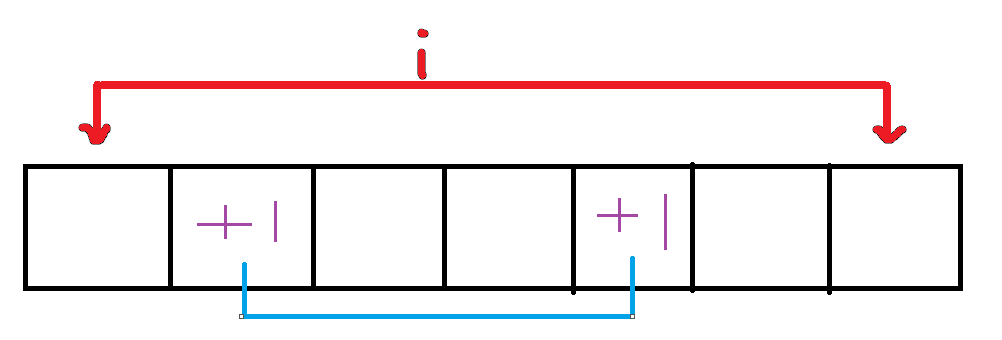
fi−2×(i−1)f_{i-2}\times (i-1)fi−2×(i−1),直接进行一次两个111位置的操作
-
剩下i−2i-2i−2长度的空序列,fi−2f_{i-2}fi−2
-
(i−1)(i-1)(i−1)次操作中,进行一次操作,Ci−11=i−1C_{i-1}^1=i-1Ci−11=i−1
-
-
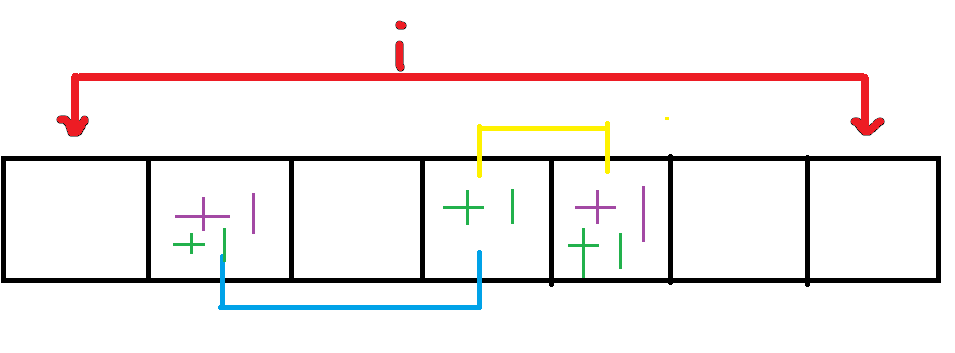
fi−3×(i−2)×Ai−12f_{i-3}\times (i-2)\times A_{i-1}^2fi−3×(i−2)×Ai−12,两个操作额外选的位置相同
-
剩下i−3i-3i−3长度的空序列,fi−3f_{i-3}fi−3
-
额外配对位置选择有(i−2)(i-2)(i−2)
-
i−1i-1i−1次操作中,两个操作的顺序不同结果不同,Ai−22A_{i-2}^2Ai−22
-
-
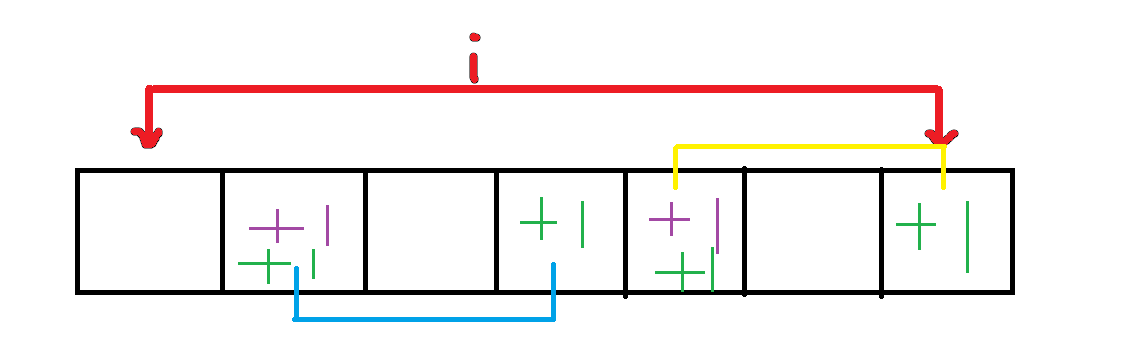
gi−2×Ai−22×Ai−12g_{i-2}\times A_{i-2}^2\times A_{i-1}^2gi−2×Ai−22×Ai−12,各自选的格子互不相同
-
剩下i−2i-2i−2长度且已有两个格子为111的序列,gi−2g_{i-2}gi−2
-
两个格子选择不同结果不同,与原两个格子的配对顺序也不同,Ai−22A_{i-2}^2Ai−22
-
i−2i-2i−2次操作中,两个操作的顺序不同结果不同,Ai−22A_{i-2}^2Ai−22
-
-
code
#include <cstdio>
#define int long long
#define maxn 10000005
#define mod 998244353
int f[maxn], g[maxn];
int n, ans;int C( int x ) {return x * ( x - 1 ) / 2 % mod;
}int A( int x ) {return x * ( x - 1 ) % mod;
}signed main() {scanf( "%lld", &n );f[0] = f[2] = g[2] = ans = 1;for( int i = 3;i <= n;i ++ ) {f[i] = ( f[i] + f[i - 2] * ( i - 1 ) % mod * C( i ) ) % mod;f[i] = ( f[i] + g[i - 1] * C( i - 1 ) % mod * A( i ) ) % mod; g[i] = ( g[i] + f[i - 2] * ( i - 1 ) ) % mod;g[i] = ( g[i] + f[i - 3] * ( i - 2 ) % mod * A( i - 1 ) ) % mod;g[i] = ( g[i] + g[i - 2] * A( i - 2 ) % mod * A( i - 1 ) ) % mod;ans = ( ans + f[i] ) % mod;}printf( "%lld\n", ans );return 0;
}
1362(div2):总结)


![P8329-[ZJOI2022]树【容斥,dp】](http://pic.xiahunao.cn/P8329-[ZJOI2022]树【容斥,dp】)
+向量内积)

)
![P6803-[CEOI2020]星际迷航【博弈论,dp,矩阵乘法】](http://pic.xiahunao.cn/P6803-[CEOI2020]星际迷航【博弈论,dp,矩阵乘法】)
成立大会暨微软技术交流会介绍》附专题视频...)



![pjudge#21655-[PR #5]双向奔赴【状压dp】](http://pic.xiahunao.cn/pjudge#21655-[PR #5]双向奔赴【状压dp】)
)
【Microsoft Entity Framework Core随笔】)



:总结)
)