Shadow Properties之美（二）【Microsoft Entity Framework Core随笔】

接着上一篇Shadow Properties之美（一），我们来继续举一个有点啰嗦的栗子。
先看简单需求：某HR系统，需要记录员工资料。需要记录的资料有：

员工号（规则：分公司所在城市拼音首字母，加上三位的顺序数字，例如 GZ001，CD001，SH007等；对于每个员工有且仅有一个员工号，且不会存在同一员工号属于不同员工的情况）；
姓；
名；
最后一次入职日期（有些员工可能会有来来回回超过一次的入职离职再入职，保存最后一次就好）
其他。。。
在继续讨论之前，会用到有关逻辑设计和物理设计的概念，它们两者的区别，建议可以先阅读一下 https://it.toolbox.com/blogs/timbryce/logical-vs-physical-design-do-you-know-the-difference-050306 ，然后我们再继续。
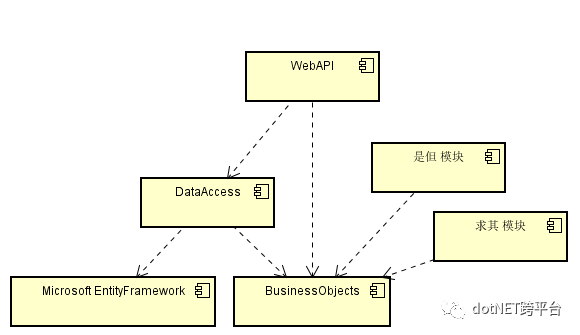
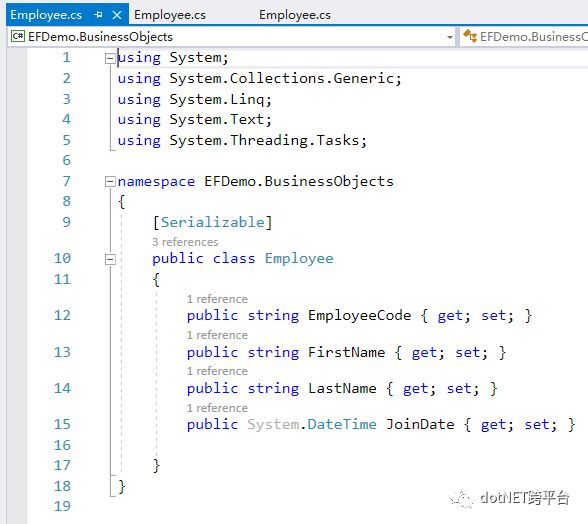
针对这个需求，我们简单地会有以下这样逻辑设计的类：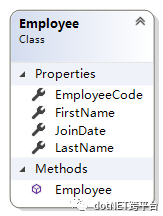
，
其中EmployeeCode就是 Unique Identifier （唯一标识符）。
（本篇的程序，可以在这里下载：https://github.com/kentliu2007/EFCoreDemo/tree/master/ShadowProperty 用的是VS 2017）
并且习惯性地会有按照 Default大法，有以下的数据表以及程序：
数据表：
、
、

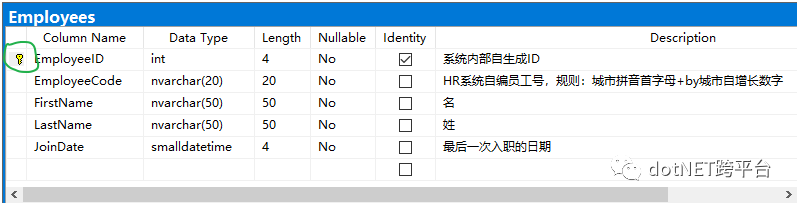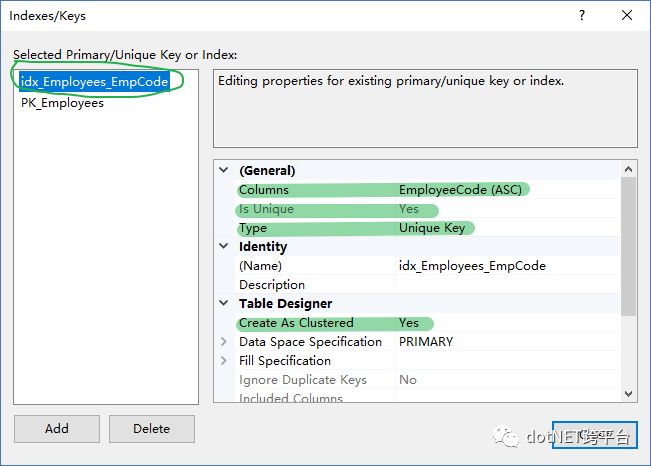
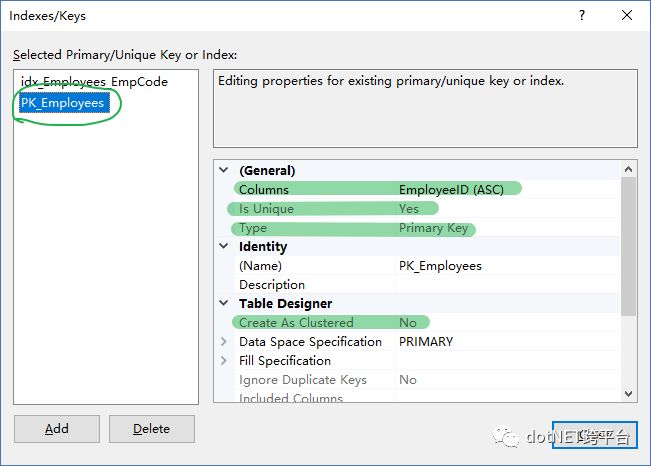
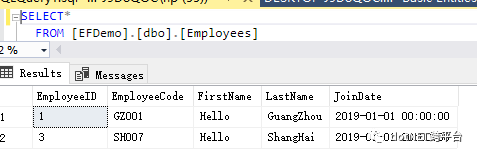
虽然default大法好，而且还可以借口 “用自增长ID来做主键，可以加快数据库做join的时候的速度”，所以才没有用 EmployeeCode来做主键（虽然这个才是Unique Identifier）。。。但是我们还是需要做一些不是完全default的改动，仔细看上面绿色标识的内容，请留意clustered index以及unique key。
演示数据：
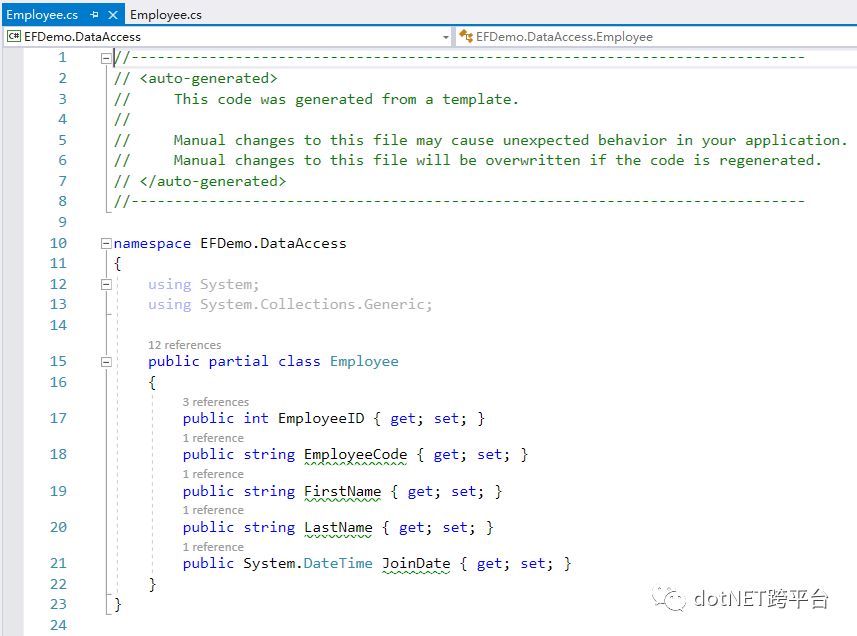
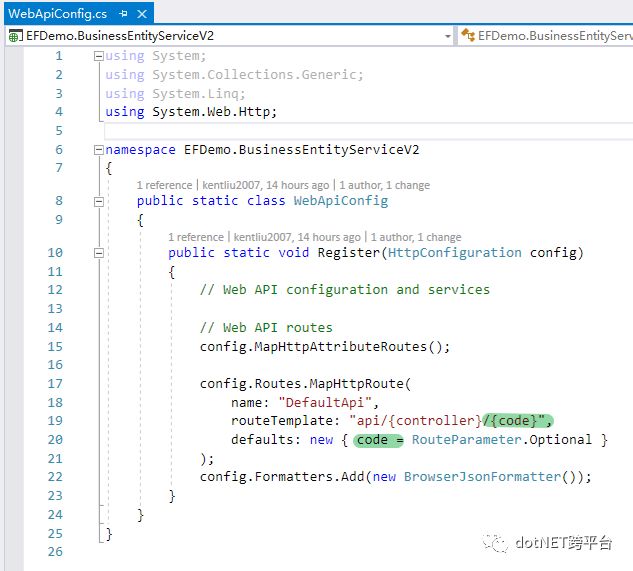
然后我们还有比较传统的基于EF6的WebApi：
、
、
、
、
、
、
、

图有点多，但是因为都按照 default 大法来捣弄的。一切都很简单很溜，对吧？

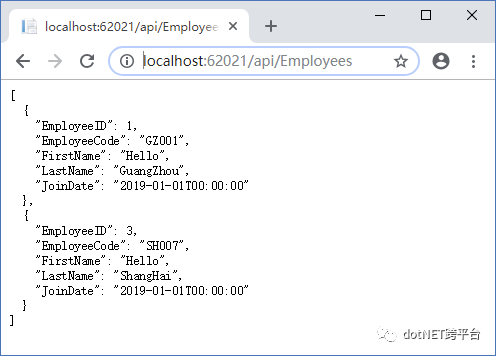
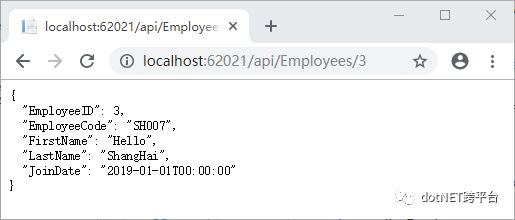
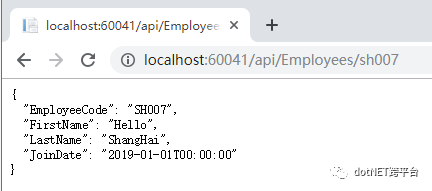
不过等等，画风有点不对，负责BDD的同事（不论是SME/BA/QC）可能会跳起来，如果我们要查询员工号是 SH007 的员工，为什么是 http://localhost:62021/api/Employees/3 ？如果换个DB，手动操作一下，或者测试并发量大的前提下，说不定要 http://localhost:62021/api/Employees/250 才是 SH007的数据了。如果换成是用GUID来做ID字段的，就可能会有类似这样的：http://localhost:62021/api/Employees/85a13f20-2d3e-4a21-807d-c64f5a55a626 ，这个又是什么鬼？其他系统call这个api的时候，或者BDD的案例描述是：查询员工号是SH007的员工的资料。。。但是我怎么知道你这个DB里面，ID是什么数字（如果是GUID的话，鬼知道又是个什么冰糖葫芦串）？麻烦请说人话好不好？这种逻辑设计里面本来就没有的，由于物理设计才出现的东西，DataAccess层，请你自己留着和数据库两个慢慢玩，不要漏出来给其他层好不好？
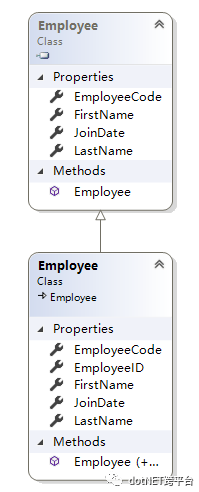
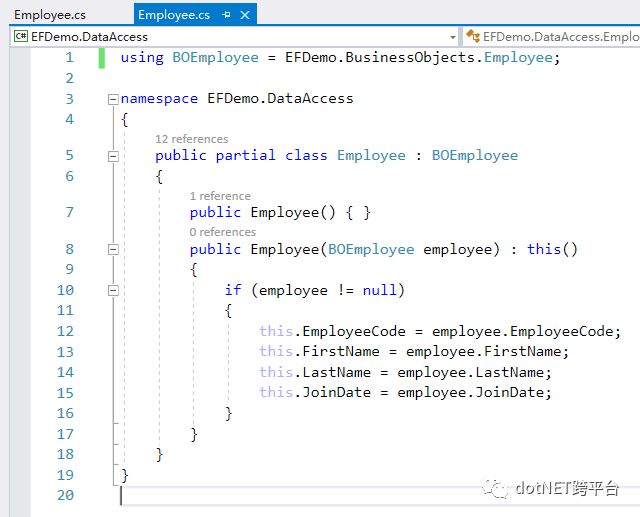
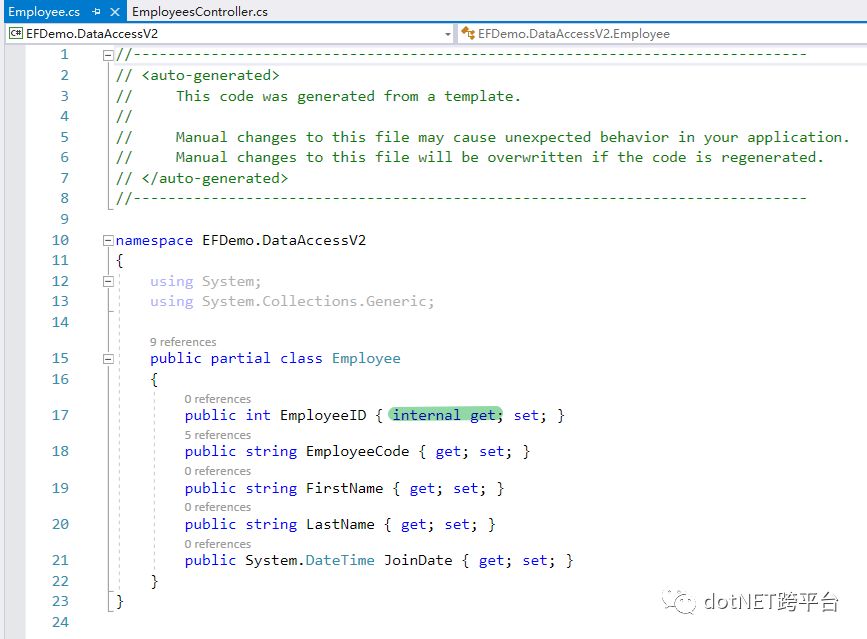
还有，俩Employee的类，有点拖沓了吧？

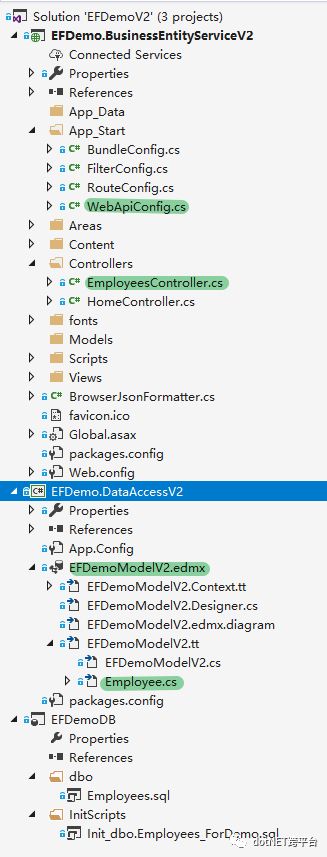
好吧，为了保持跟逻辑层一致，并且不想要两个employee类，继续使用EF6，我们会有第二个版本：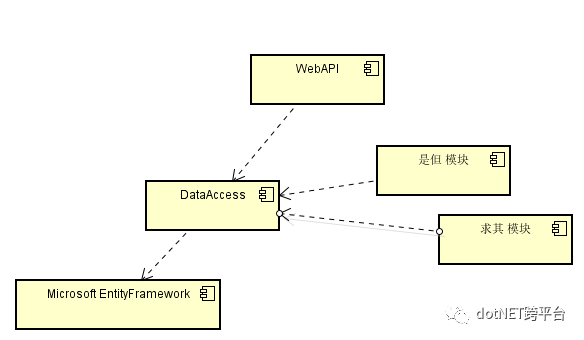
640?wx_fmt=png 、
、
、
、
、

这下画风正常了。不过一堆模块都需要引用或者基于 DataAccess 模块；还有虽然只有一个employee类了，但是还要加上一些其他internal的属性。。。总感觉还是做得不够优雅（混了牛奶和糖的美式啊）。

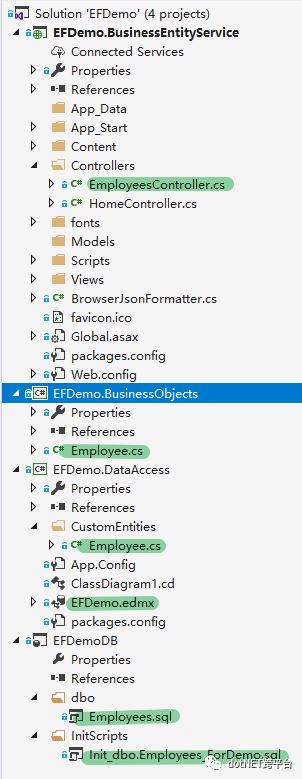
现在有了EF Core的Shadow Property，我们可以把这个做得很优雅（鼓掌）。Shadow Property就是让我们可以保持逻辑设计层美式的纯正，然后让 DataAccess层可以处理和消化掉物理设计层特有的元素：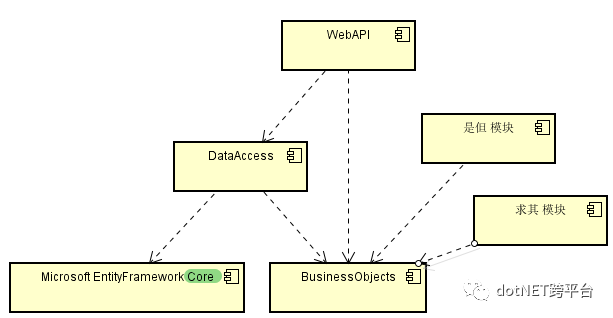
640?wx_fmt=png 、
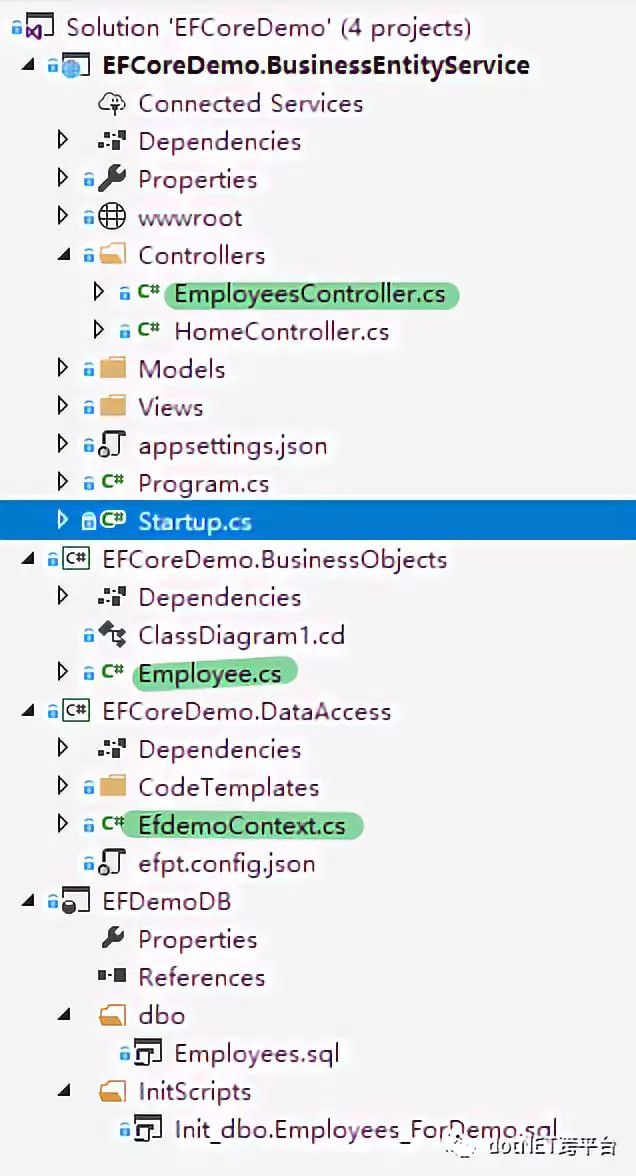640?wx_fmt=jpeg 、
、
、
、

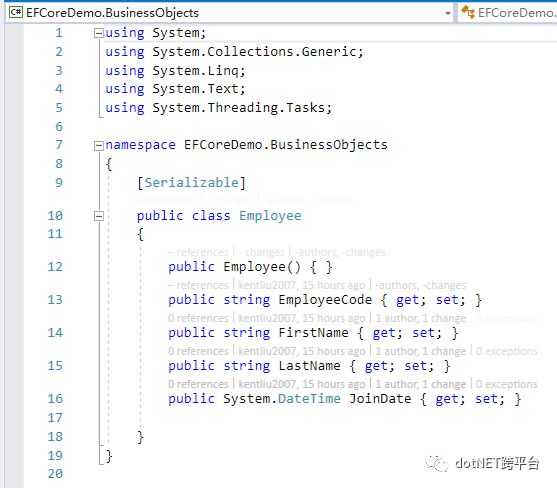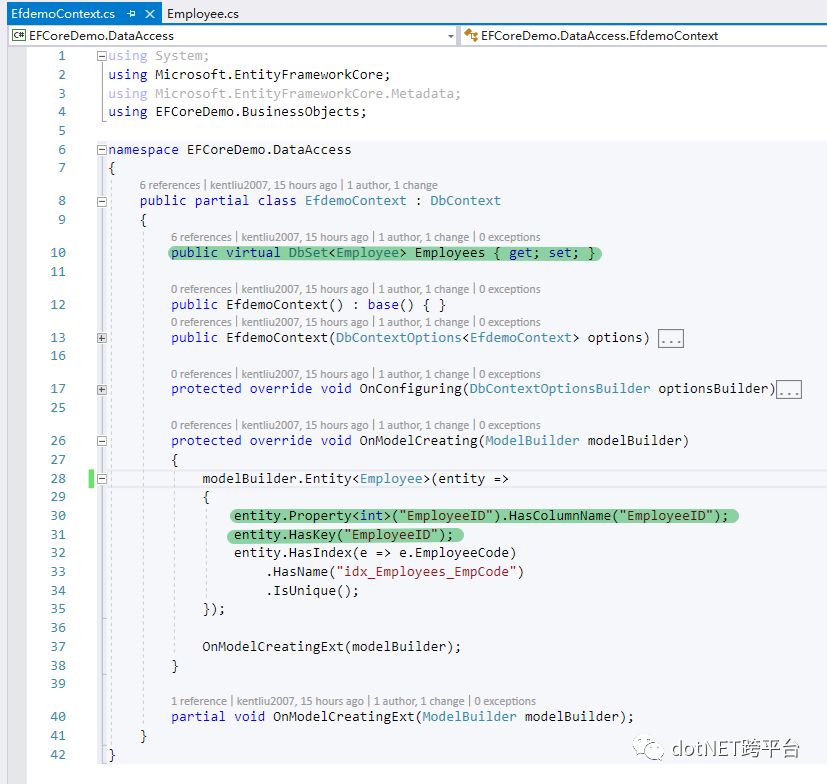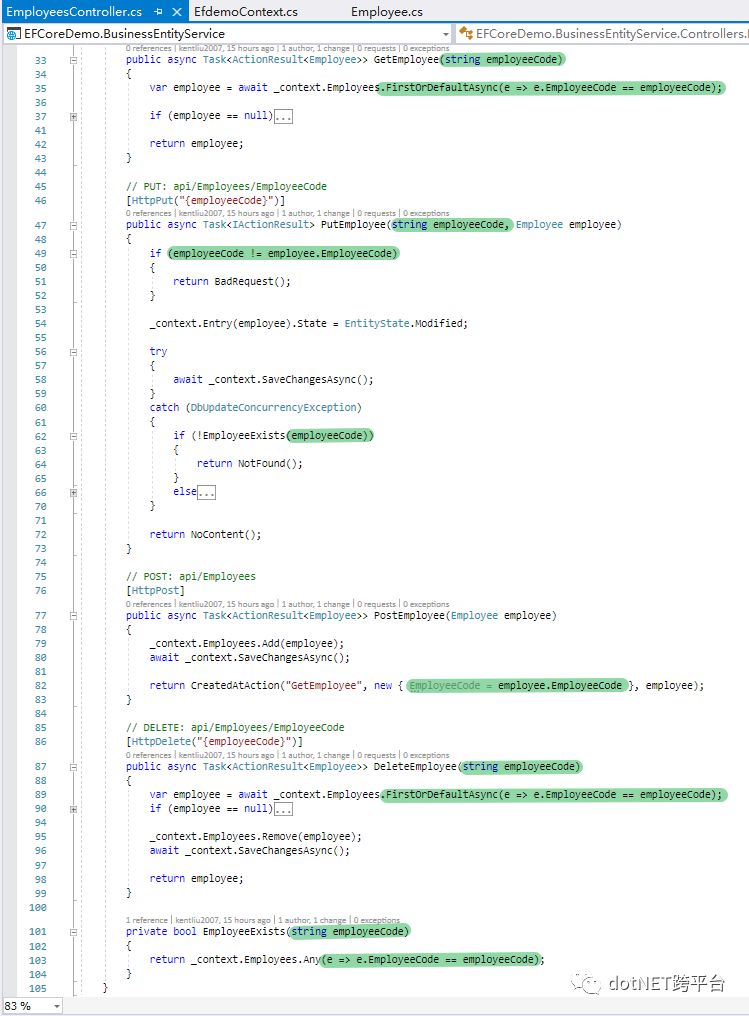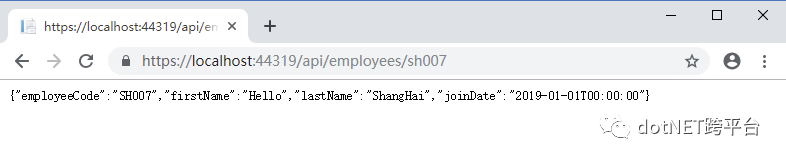
看，一切都很 “美式” 的优雅，不存在骗奶骗糖的感觉：从Component Diagram来看，各个模块都引用着正确的逻辑设计模块；DataAccess模块没有需要多产生一个拖沓的EF类；外部系统以及人机对话的时候，都是针对逻辑设计来交谈，且说的都是人话。