ICPC网络赛第二场G Limit

题意：

给你数组a和b，求解：
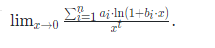
在这里插入图片描述
$1≤n≤100000,−100≤a_{i},b_{i}≤100,0≤t≤5.$

题解：

要用到洛必达来做，首先明确一下，洛必达要求分母分子都趋于0
什么情况是无穷？分母无限趋于0，分子为常数时，此时就是无穷情况
那我们可以这样做，直接将式子洛必达t次，每次洛必达结束后判断，如果分母无限趋于0(即还存在x)，分母为常数(说明分母洛必达后的系数不为0)，此时答案就是 $\infty$
否则，答案就是常数
分母洛必达好求
分子洛必达为：
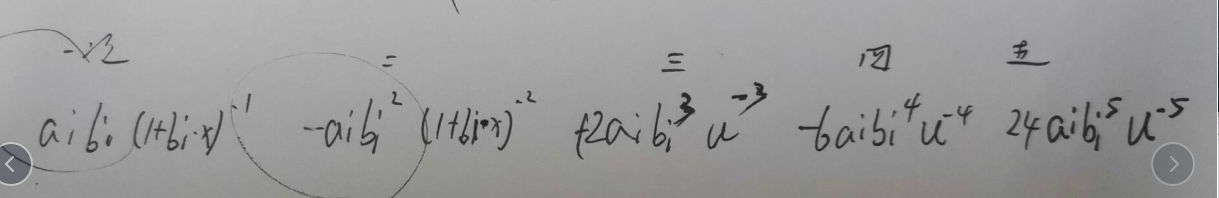
请添加图片描述
对于每次洛必达，我们就求对应的数是否为0(比如第一次洛必达后，就是求 $∑aibi\sum{a_{i}b_{i}}$ )

代码：

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define x first
#define y second
typedef pair<int,int> pii;
const int N = 400010;
const int mod=998244353;
int a[N];
int b[N];
int main()
{int n;cin>>n;int t;cin>>t;for(int i=1;i<=n;i++)	cin>>a[i]>>b[i];if(t==0){cout<<0<<endl;}else{int now=0;int d=1;for(int i=1;i<=t;i++){now=0;d*=i;if(i==1){				for(int j=1;j<=n;j++)now=now+a[j]*b[j];}else if(i==2){for(int j=1;j<=n;j++)now=now+a[j]*b[j]*b[j]*(-1);}else if(i==3){for(int j=1;j<=n;j++)now=now+a[j]*b[j]*b[j]*2*b[j];}else if(i==4){for(int j=1;j<=n;j++)now=now+a[j]*b[j]*b[j]*(-6)*b[j]*b[j];}else{for(int j=1;j<=n;j++)now=now+a[j]*b[j]*b[j]*24*b[j]*b[j]*b[j];}
//			cout<<"now="<<now<<endl;if(now!=0 && i!=t){cout<<"infinity"<<endl;return 0;}}int g=__gcd(now,d);now/=g;d/=g;if(d==1)	cout<<now<<endl;else	cout<<now<<"/"<<d<<endl;}return 0;}