CF1479C Continuous City

题意：

给定 L, R. 构造一个有向带权图, 其中点数不大于 32, 且所有边都是从较小的点指向较大的点. 假设这个有向图有 n 个点, 你需要保证从 1到n 的所有路径的权值都在 [L, R]内且不存在 x∈[L,R], 使得不存在或存在多于一条从 1 到 n 的路径权值为 x, 或者断言这是不可能的.

题解：

点数不超过32，其实就在往二进制的方向引，但是想了半天也没头绪
看了海量题解，终于悟出一些
参考文章
首先无论如何都有解，$lo{g}_2(1e6)=19.931569$,一共用22个点就够了(20个中间点+出发点+结束点)
题目要求构造值域为[L，R]的路径长度，我们先从1号点向所有点连一条长度为L的边，现在的问题就是如何构造出值域[1,R-L]的路径长度
对于所有中间点$i\in [2,21]$，我们可以认为第i个点代表二进制的第i-2位，从i号点向其他点(不含结束点)连一条长度为$2^{i-2}$的边
如图，(相同颜色权值一样，绿色和黄色未画完全)，点2到点21可以表示出路径长度的值域为$[1,2^{i-2}-1]$,你可以这么理解，二进制下，走一条边相当于对应的第i-2位是1，如果你从2走到3，在走到4，相当于权值为111(二进制)，如果一直走到点21，权值不就是$2^{i-2}-1$
再加上之前的L，此时1→i的路径长度值域为$[L,L+2^{i-2}-1]$

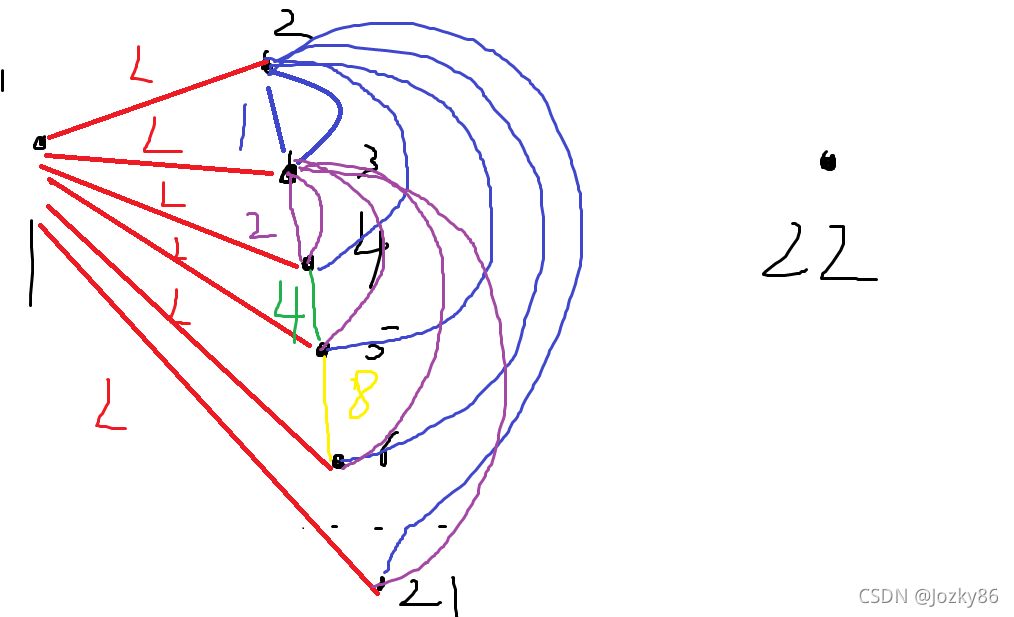
现在问题在于$L+2^{i-2}-1$又不是R,现在我们开始考虑如何凑出R-L
(还是先忽略L)，我们用第22号点当作n号点
枚举$i\in [2,21]$，如果R-L第i-2位是1，令t表示将R-L末i-2位都修改为0后的值，然后我们就从i向n号点连一条权值为t+1的边。可以理解成我们将缺失那部分拆成两部分，一部分可以用之前已经构造好的二进制来实现，另一部分作为权值再建新边，这样组合正好就是我们需要的值
一下01都是二进制下，
比如R-L值为101(二进制)，第0位是1，所以我们就从点2向点22建边，边权为101-1+1，第2位是1，所以我们从点4向点22建边，边权为101-101+1，这样我们就可以构造出[L,R]。因为我之前构造边权都是点2到点21之间的，现在R-L的第i位是1，就将第i-2个点连向n，因为第i+2个点最大值域到$2^{i-2}$，所以边权为$(R-L)-2^{i-2}+1$
比如样例[4,9]，根据我讲的方法构造如图：

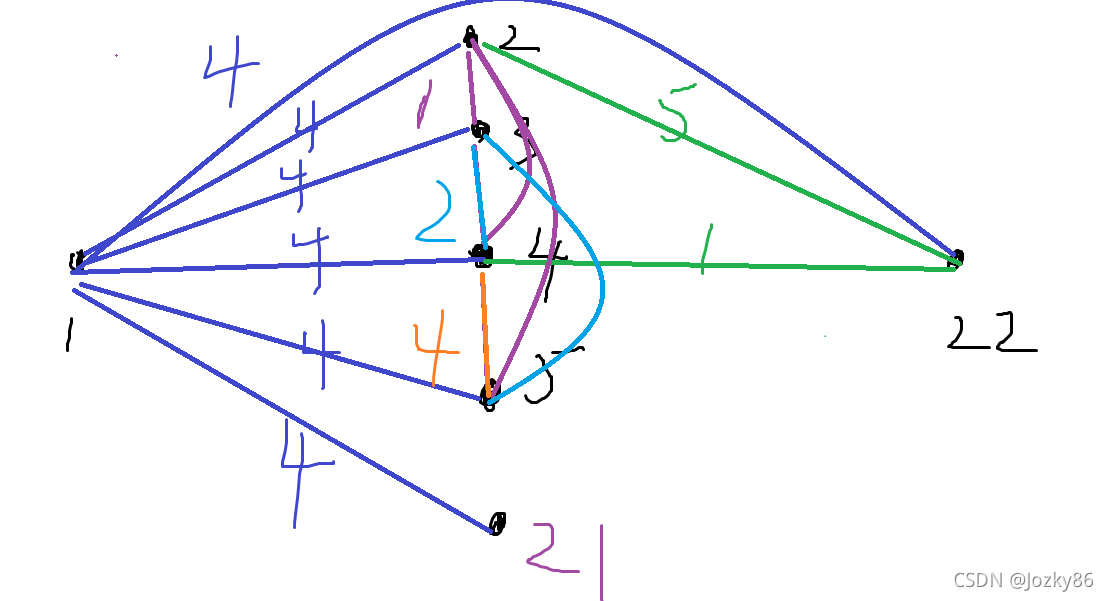
感性再理解理解，确实不好想

代码：

#include <bits/stdc++.h>
#include <unordered_map>
#define debug(a, b) printf("%s = %d\n", a, b);
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> PII;
clock_t startTime, endTime;
//Fe~Jozky
const ll INF_ll= 1e18;
const int INF_int= 0x3f3f3f3f;
void read(){};
template <typename _Tp, typename... _Tps> void read(_Tp& x, _Tps&... Ar)
{x= 0;char c= getchar();bool flag= 0;while (c < '0' || c > '9')flag|= (c == '-'), c= getchar();while (c >= '0' && c <= '9')x= (x << 3) + (x << 1) + (c ^ 48), c= getchar();if (flag)x= -x;read(Ar...);
}
template <typename T> inline void write(T x)
{if (x < 0) {x= ~(x - 1);putchar('-');}if (x > 9)write(x / 10);putchar(x % 10 + '0');
}
void rd_test()
{
#ifdef ONLINE_JUDGE
#elsestartTime = clock ();freopen("data.in", "r", stdin);
#endif
}
void Time_test()
{
#ifdef ONLINE_JUDGE
#elseendTime= clock();printf("\nRun Time:%lfs\n", (double)(endTime - startTime) / CLOCKS_PER_SEC);
#endif
}
int L,R,cnt,tot;
const int maxn=2e6+9;
struct node{int x,y,z;
};
vector<node>vec;
int main()
{scanf("%d%d",&L,&R);puts("YES");vec.push_back({1,22,L});//从1号点向n号点连边for(int i=1;i<=20;++i){for(int j=i+1;j<=21;++j){int t;if(i!=1)t=1<<i-2;else t=L;vec.push_back({i,j,t});//从1~20号点向之后除n号点以外的点连边}}int t=R-L;for(int i=2;i<=21;++i){if(t>>(i-2)&1){t^=(1<<i-2);vec.push_back({i,22,t+1});}}printf("22 %d\n",vec.size());for(int i=0;i<vec.size();i++){printf("%d %d %d\n",vec[i].x,vec[i].y,vec[i].z);}return 0;//输出构造方案
}