传送门
这场比较简单,简单的题就不说题意了。
A.
问加nnn个数,能否使a,b,ca,b,ca,b,c相等。
直接先加到相等再看看模333是否为000即可。
//#pragma GCC optimize(2)
#include<cstdio>
#include<iostream>
#include<string>
#include<cstring>
#include<map>
#include<cmath>
#include<cctype>
#include<vector>
#include<set>
#include<queue>
#include<algorithm>
#include<sstream>
#include<ctime>
#include<cstdlib>
#define X first
#define Y second
#define L (u<<1)
#define R (u<<1|1)
#define pb push_back
#define mk make_pair
#define Mid (tr[u].l+tr[u].r>>1)
#define Len(u) (tr[u].r-tr[u].l+1)
#define random(a,b) ((a)+rand()%((b)-(a)+1))
#define db puts("---")
using namespace std;//void rd_cre() { freopen("d://dp//data.txt","w",stdout); srand(time(NULL)); }
//void rd_ac() { freopen("d://dp//data.txt","r",stdin); freopen("d://dp//AC.txt","w",stdout); }
//void rd_wa() { freopen("d://dp//data.txt","r",stdin); freopen("d://dp//WA.txt","w",stdout); }typedef long long LL;
typedef unsigned long long ULL;
typedef pair<int,int> PII;const int N=1000010,mod=1e9+7,INF=0x3f3f3f3f;
const double eps=1e-6;int a[10];int main()
{
// ios::sync_with_stdio(false);
// cin.tie(0);int _; scanf("%d",&_);while(_--){int n;scanf("%d%d%d%d",&a[1],&a[2],&a[3],&n);sort(a+1,a+1+3);n-=a[3]-a[1];n-=a[3]-a[2];if(n<0||n%3!=0) puts("NO");else puts("YES");}return 0;
}
/**/B.
只能往右或者上走,求字典序最小的走法。
排序后判一下是否有不合法的点,让后每次都先右后上就行。
//#pragma GCC optimize(2)
#include<cstdio>
#include<iostream>
#include<string>
#include<cstring>
#include<map>
#include<cmath>
#include<cctype>
#include<vector>
#include<set>
#include<queue>
#include<algorithm>
#include<sstream>
#include<ctime>
#include<cstdlib>
#define X first
#define Y second
#define L (u<<1)
#define R (u<<1|1)
#define pb push_back
#define mk make_pair
#define Mid (tr[u].l+tr[u].r>>1)
#define Len(u) (tr[u].r-tr[u].l+1)
#define random(a,b) ((a)+rand()%((b)-(a)+1))
#define db puts("---")
using namespace std;//void rd_cre() { freopen("d://dp//data.txt","w",stdout); srand(time(NULL)); }
//void rd_ac() { freopen("d://dp//data.txt","r",stdin); freopen("d://dp//AC.txt","w",stdout); }
//void rd_wa() { freopen("d://dp//data.txt","r",stdin); freopen("d://dp//WA.txt","w",stdout); }typedef long long LL;
typedef unsigned long long ULL;
typedef pair<int,int> PII;const int N=100010,mod=1e9+7,INF=0x3f3f3f3f;
const double eps=1e-6;int n;
PII p[N];bool check()
{for(int i=2;i<=n;i++) if(p[i].X<p[i-1].X||p[i].Y<p[i-1].Y) return false;return true;
}int main()
{
// ios::sync_with_stdio(false);
// cin.tie(0);int _; scanf("%d",&_);while(_--){scanf("%d",&n);for(int i=1;i<=n;i++) scanf("%d%d",&p[i].X,&p[i].Y);sort(p+1,p+1+n);if(check()){puts("YES");int sx=0,sy=0,st=1;while(st<=n){for(int i=sx;i<p[st].X;i++) printf("R");for(int i=sy;i<p[st].Y;i++) printf("U");sx=p[st].X; sy=p[st].Y;st++;}puts("");}else puts("NO");}return 0;
}
/**/C.
找三个数a,b,ca,b,ca,b,c,且其都大于等于222,且a!=b,b!=c,a!=ca!=b,b!=c,a!=ca!=b,b!=c,a!=c,且a∗b∗c=na*b*c=na∗b∗c=n。
直接把nnn质因子分解,让后按照质因子的幂次从1,2,3...1,2,3...1,2,3...累乘起来,取两个数,第三个数直接算即可。
//#pragma GCC optimize(2)
#include<cstdio>
#include<iostream>
#include<string>
#include<cstring>
#include<map>
#include<cmath>
#include<cctype>
#include<vector>
#include<set>
#include<queue>
#include<algorithm>
#include<sstream>
#include<ctime>
#include<cstdlib>
#define X first
#define Y second
#define L (u<<1)
#define R (u<<1|1)
#define pb push_back
#define mk make_pair
#define Mid (tr[u].l+tr[u].r>>1)
#define Len(u) (tr[u].r-tr[u].l+1)
#define random(a,b) ((a)+rand()%((b)-(a)+1))
#define db puts("---")
using namespace std;//void rd_cre() { freopen("d://dp//data.txt","w",stdout); srand(time(NULL)); }
//void rd_ac() { freopen("d://dp//data.txt","r",stdin); freopen("d://dp//AC.txt","w",stdout); }
//void rd_wa() { freopen("d://dp//data.txt","r",stdin); freopen("d://dp//WA.txt","w",stdout); }typedef long long LL;
typedef unsigned long long ULL;
typedef pair<int,int> PII;const int N=100010,mod=1e9+7,INF=0x3f3f3f3f;
const double eps=1e-6;int n;
map<int,int>mp;void divide()
{for(int i=2;i<=n/i;i++)if(n%i==0){while(n%i==0) mp[i]++,n/=i;}if(n>1) mp[n]++;
}int main()
{
// ios::sync_with_stdio(false);
// cin.tie(0);int _; scanf("%d",&_);while(_--){scanf("%d",&n);int nn=n;mp.clear();divide();int a,b,c;a=-1; b=-1; c=-1;vector<int>v;for(auto x:mp){int now=x.X,cnt=1;while(cnt<=x.Y){v.pb(now);now*=x.X;x.Y-=cnt;cnt++;}}if(v.size()<2) puts("NO");else{a=v[0],b=v[1],c=nn/a/b;if(c==1||c==a||c==b) { puts("NO"); continue; }puts("YES");printf("%d %d %d\n",a,b,c);}}return 0;
}
/**/D.
序列初始为空,每次加入一个数yyy,可以将这个数+x,−x+x,-x+x,−x,可以执行无限次,但是yyy不能小于000。求每次加入数后的最大mexmexmex。
因为求最大的mexmexmex,所以肯定是将这个数从小往大的填。我们将ymodxy\bmod xymodx,这个时候可以将其看成一个系,即ymodx+k∗xy\bmod x +k*xymodx+k∗x,我们从这个系的底开始向上填即可。由于ymodx<xy\bmod x<xymodx<x只需要开一个数组记录一下当前底是多少,每次如果用掉了就让这个底+x+x+x即可。
但是注意不能一直加,这样的话会rerere,所以我们设置一个上限就好啦,因为mexmexmex不会一直大下去的。
//#pragma GCC optimize(2)
#include<cstdio>
#include<iostream>
#include<string>
#include<cstring>
#include<map>
#include<cmath>
#include<cctype>
#include<vector>
#include<set>
#include<queue>
#include<algorithm>
#include<sstream>
#include<ctime>
#include<cstdlib>
#define X first
#define Y second
#define L (u<<1)
#define R (u<<1|1)
#define pb push_back
#define mk make_pair
#define Mid (tr[u].l+tr[u].r>>1)
#define Len(u) (tr[u].r-tr[u].l+1)
#define random(a,b) ((a)+rand()%((b)-(a)+1))
#define db puts("---")
using namespace std;//void rd_cre() { freopen("d://dp//data.txt","w",stdout); srand(time(NULL)); }
//void rd_ac() { freopen("d://dp//data.txt","r",stdin); freopen("d://dp//AC.txt","w",stdout); }
//void rd_wa() { freopen("d://dp//data.txt","r",stdin); freopen("d://dp//WA.txt","w",stdout); }typedef long long LL;
typedef unsigned long long ULL;
typedef pair<int,int> PII;const int N=10000010,mod=1e9+7,INF=0x3f3f3f3f;
const double eps=1e-6;int q,x;
int pos[N],st[N];
int ans=0;int main()
{
// ios::sync_with_stdio(false);
// cin.tie(0);scanf("%d%d",&q,&x);for(int i=0;i<=x;i++) pos[i]=i;while(q--){int v; scanf("%d",&v);v%=x; if(pos[v]<8000000) pos[v]+=x; v=pos[v]-x;st[v]=1;while(st[ans]) ans++;printf("%d\n",ans);}return 0;
}
/**/E.
给你个矩阵,每次可以修改一个数为1,n∗m1,n*m1,n∗m之间的任何数,也可以将一列向上循环移动一位,这两个花费都是111,求变成如下矩阵的最小花费。
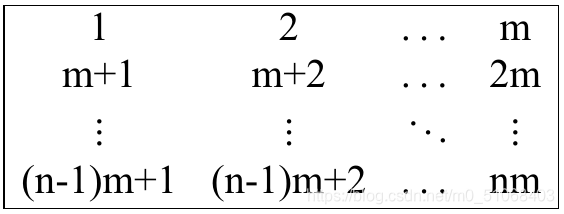
乍一看不是很好做,但是仔细一想就是个大水题。
因为移动只涉及列,所以每一列是独立的,我们独立统计每一列就好啦。
只考虑一列,我们可以记录一下这一列的每个数,这个数到他应该到的位置需要移动几次,假设移动xxx次,让后我们让cnt[x]++cnt[x]++cnt[x]++,之后就枚举移动几次,假设移动iii次,让后答案就是n−cnt[x]+in-cnt[x]+in−cnt[x]+i。
//#pragma GCC optimize(2)
#include<cstdio>
#include<iostream>
#include<string>
#include<cstring>
#include<map>
#include<cmath>
#include<cctype>
#include<vector>
#include<set>
#include<queue>
#include<algorithm>
#include<sstream>
#include<ctime>
#include<cstdlib>
#define X first
#include<assert.h>
#define Y second
#define L (u<<1)
#define R (u<<1|1)
#define pb push_back
#define mk make_pair
#define Mid (tr[u].l+tr[u].r>>1)
#define Len(u) (tr[u].r-tr[u].l+1)
#define random(a,b) ((a)+rand()%((b)-(a)+1))
#define db puts("---")
using namespace std;//void rd_cre() { freopen("d://dp//data.txt","w",stdout); srand(time(NULL)); }
//void rd_ac() { freopen("d://dp//data.txt","r",stdin); freopen("d://dp//AC.txt","w",stdout); }
//void rd_wa() { freopen("d://dp//data.txt","r",stdin); freopen("d://dp//WA.txt","w",stdout); }typedef long long LL;
typedef unsigned long long ULL;
typedef pair<int,int> PII;const int N=2000010,mod=1e9+7,INF=0x3f3f3f3f;
const double eps=1e-6;int n,m;
int a[N];
vector<int>v[N];int solve(int j)
{for(int i=0;i<=n;i++) a[i]=0;for(int i=0;i<n;i++){if(v[i][j]%m!=j||v[i][j]>=n*m) continue;int pos=v[i][j]/m;int cnt=0;if(pos>i) cnt=i+n-pos;else cnt=i-pos;a[cnt]++;}int ans=INF;for(int i=0;i<=n;i++) ans=min(ans,i+n-a[i]);return ans;
}int main()
{
// ios::sync_with_stdio(false);
// cin.tie(0);scanf("%d%d",&n,&m);for(int i=0;i<n;i++)for(int j=0;j<m;j++){int x; scanf("%d",&x); x--;v[i].pb(x);}int ans=0;for(int i=0;i<m;i++) ans+=solve(i);printf("%d\n",ans);return 0;
}
/**/F.
求三个点,这三个点之间的边最多。
众所周知,cfcfcf就是猜结论的比赛。所以直接选两个点为直径的两端,之后选的一个点就是到直径边最多的点即可。
实现的话我以前写过求直径上所有点的,所以直接贴过来了,知道所有点了之后,放进队列,bfsbfsbfs求disdisdis,选个disdisdis最大的即可。
//#pragma GCC optimize(2)
#include<cstdio>
#include<iostream>
#include<string>
#include<cstring>
#include<map>
#include<cmath>
#include<cctype>
#include<vector>
#include<set>
#include<queue>
#include<algorithm>
#include<sstream>
#include<ctime>
#include<cstdlib>
#define X first
#define Y second
#define L (u<<1)
#define R (u<<1|1)
#define pb push_back
#define mk make_pair
#define Mid (tr[u].l+tr[u].r>>1)
#define Len(u) (tr[u].r-tr[u].l+1)
#define random(a,b) ((a)+rand()%((b)-(a)+1))
#define db puts("---")
using namespace std;//void rd_cre() { freopen("d://dp//data.txt","w",stdout); srand(time(NULL)); }
//void rd_ac() { freopen("d://dp//data.txt","r",stdin); freopen("d://dp//AC.txt","w",stdout); }
//void rd_wa() { freopen("d://dp//data.txt","r",stdin); freopen("d://dp//WA.txt","w",stdout); }typedef long long LL;
typedef unsigned long long ULL;
typedef pair<int,int> PII;const int N=1000010,M=N*2,mod=1e9+7,INF=0x3f3f3f3f;
const double eps=1e-6;int n,root;
map<PII,int>mp;
vector<int>v[N];
int ans[N],d[N],dis[N];
int e[M],ne[M],h[N],w[M],idx;
int depth[N],res;
bool st[N];
int ed,flag,pre[N];void add(int a,int b,int c)
{e[idx]=b,w[idx]=c,ne[idx]=h[a],h[a]=idx++;
}void dfs_dep(int u,int fa)
{depth[u]=depth[fa]+1;for(auto x:v[u]){int ver=x;if(ver==fa) continue;dfs_dep(ver,u);}
}void dfs(int u,int fa)
{if(flag) return;if(u==ed) { flag=1; return; }for(auto x:v[u]){if(x==fa) continue;pre[x]=u;dfs(x,u);if(flag) return;pre[x]=0;}
}void dfs_add(int u,int fa)
{for(auto x:v[u]){if(x==fa) continue;ans[x]=mp[{x,u}];dfs_add(x,u);}
}void dfs_d(int u,int fa)
{int mx=0;for(auto x:v[u]){if(x==fa) continue;dfs_d(x,u);mx=max(mx,depth[x]+1);}depth[u]=mx;
}int main()
{
// ios::sync_with_stdio(false);
// cin.tie(0);memset(h,-1,sizeof(h));scanf("%d",&n);for(int i=1;i<=n-1;i++){int a,b; scanf("%d%d",&a,&b);v[a].pb(b),v[b].pb(a);}dfs_dep(1,0);int id=0,mx=-1;for(int i=1;i<=n;i++) if(depth[i]>mx) mx=depth[i],root=i;memset(depth,0,sizeof(depth));dfs_dep(root,0); mx=-1;for(int i=1;i<=n;i++) if(depth[i]>mx) mx=depth[i],ed=i;dfs(root,0);vector<int>vv; vv.pb(ed);pre[root]=0;while(pre[ed]!=0) vv.pb(pre[ed]),ed=pre[ed];queue<int>q;memset(dis,0x3f,sizeof(dis));memset(st,false,sizeof(st));for(int i=0;i<vv.size();i++) { int x=vv[i]; q.push(x),st[x]=1,dis[x]=0; }while(q.size()){int t=q.front(); q.pop();for(int i=0;i<v[t].size();i++){int x=v[t][i];if(st[x]) continue;dis[x]=dis[t]+1;st[x]=1;q.push(x);}}int x=vv[0],y=vv[vv.size()-1],z=vv[1];int mmx=0;for(int i=1;i<=n;i++) if(dis[i]>mmx&&dis[i]!=INF) mmx=dis[i],z=i;printf("%d\n",mmx+(int)vv.size()-1);printf("%d %d %d\n",x,y,z);return 0;
}
/*
12
1 2
2 12
2 3
12 7
12 6
12 5
3 4
1 11
11 8
11 9
11 10
*/
)
 F. Berland Beauty 思维)

 D(倍增dp))

 E2. String Coloring (hard version) 思维 + dp + Dilworth定理)
 D(随机算法))
 D. Cut and Stick 主席树 + 思维)




 F. Flip the Cards 思维 + 贪心)

![[牛客] Tree-换根dp(预防加法取模导致等0)](http://pic.xiahunao.cn/[牛客] Tree-换根dp(预防加法取模导致等0))
 F.Good Contest \ 洛谷 划艇 组合 计数dp)
)

 D. Cut 倍增)