1：transient
当对象被序列化时，transient阻止其修饰的对象进行序列化；当反序列化时，此对象的值不会被恢复。
2：instanceof
判断引用指向的对象，是不是某个类及其子类的实例对象；
class Person {}public class Man extends Person {public static void main(String[] args) {if("111" instanceof String) {System.out.println("所有字符串都是String类型");}Person man = null;//尚未初始化，指向的对象为null，不是任何类的对象if(man instanceof Man) {System.out.println("man 是Man的对象");}if(man instanceof Person) {System.out.println("man 是Person的对象");}man = new Man();//初始化之后if(man instanceof Man) {System.out.println("man 是Man的对象");}if(man instanceof Person) {System.out.println("man 是Person的对象");}}}
输出如下：
所有字符串都是String类型
man 是Man的对象
man 是Person的对象
3：volatile
volatile是Java提供的轻量级的线程同步机制，与之相对，synchronized通常被称为重量级锁。
volatile有两个特性：
-
保证共享变量对所有线程的可见性；
-
禁止指令重排序优化；
Java多线程内存模型简要描述如下：
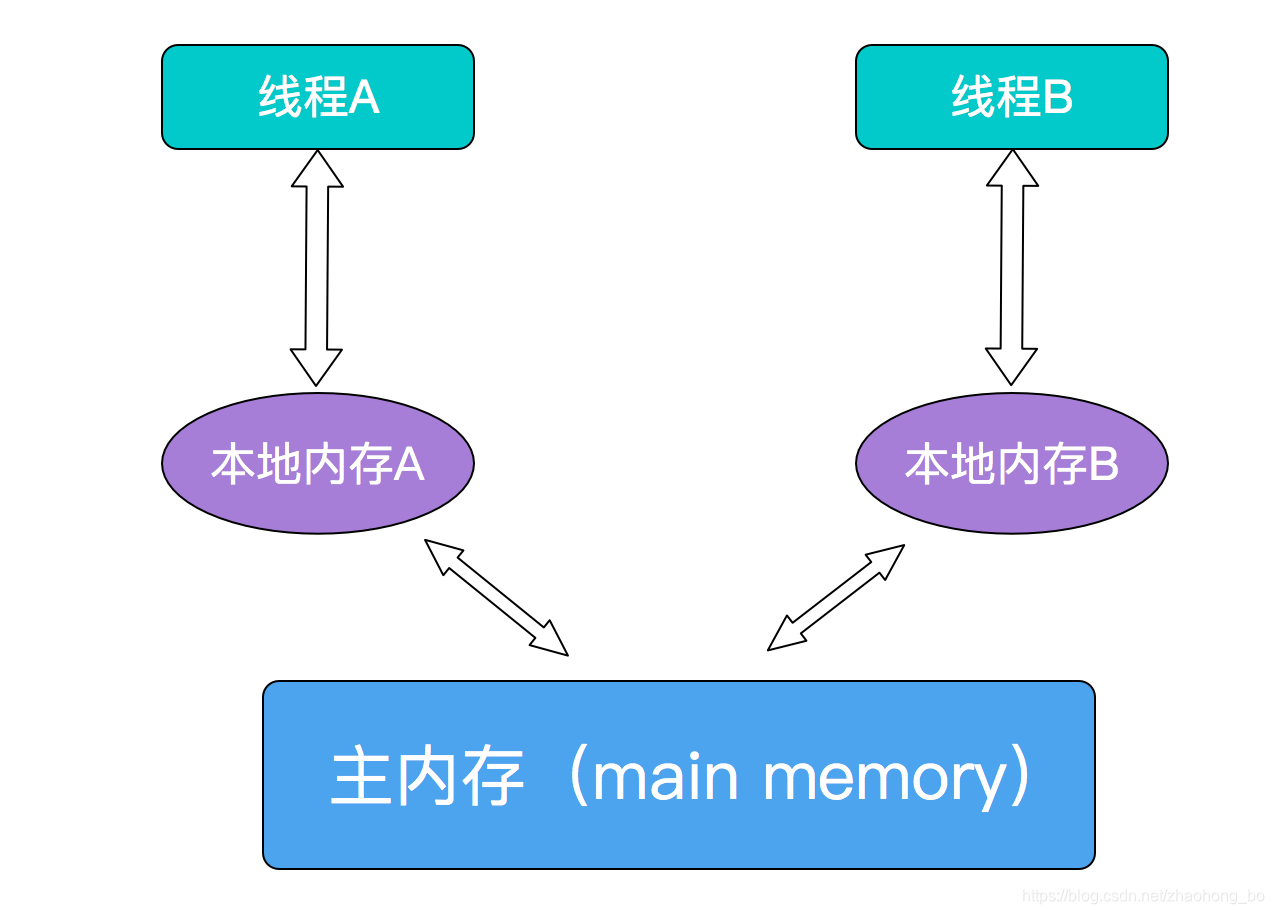
volatile保证可见性的方式为： -
当写一个共享变量时，JMM（Java Memory Model）会把该线程对应的本地内存中的变量强制刷新到主内存中；
-
这个写操作会导致其他线程的本地内存中的缓存无效；
对于num++这类的复合操作，只使用volatile无法保证其原子性；可以通过synchronized或其他的锁机制、CAS机制来保障（参见后续文章）
volatile禁止指令重排序：
volatile修饰变量，在编译时，会在指令序列中插入内存屏障来禁止特定类型的处理器重排序；
volatile禁止指令重排序的一些规则：
- 当第二个操作是volatile写时，无论第一个操作是什么，都不能进行重排序；
- 当第一个操作是volatile读时，无论第二个操作是什么，都不能进行重排序；
- 当第一个操作是volatile写，第二个操作是volatile读时，不能进行重排序；
3.1：volatile拓展，Java JMM的happens-before原则规则：
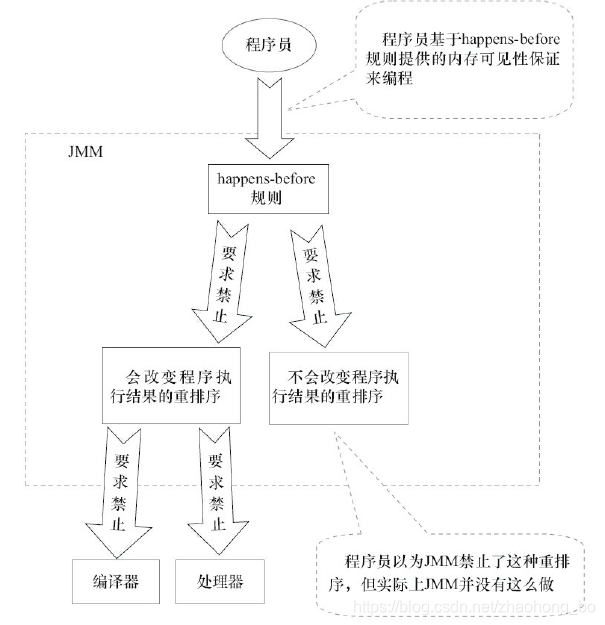
《JSR-133:Java Memory Model and Thread Specification》对happens-before关系的定义如下：
1.如果一个操作happens-before另一个操作，那么第一个操作的执行结果将对第二个操作可见，而且第一个操作的执行顺序排在第二个操作之前。
2.两个操作之间存在happens-before关系，并不意味着Java平台的具体实现必须要按照happens-before关系指定的顺序来执行。如果重排序之后的执行结果，与按happens-before关系来执行的结果一致，那么这种重排序并不非法。
上面1是JMM对程序员的承诺。从程序员的角度来说，可以这样理解happens-before关系：如果A happens-before B，那么Java内存模型将向程序员保证——A操作的结果将对B可见，且A的执行顺序排在B之前。注意，这只是Java内存模型向程序员做出的保证！
上面2是JMM对编译器和处理器冲排序的约束。MM其实是在遵循一个基本原则：只要不改变程序的执行结果，编译器和处理器怎么优化都行。happens-before这么做的目的，都是为了在不改变程序执行结果的前提下，尽可能地提高程序执行的并行度。
三.happens-before规则
1.程序顺序规则：一个线程中的每个操作，happens-before于该线程中的任意后续操作
2.监视器锁规则：对一个锁的解锁，happens-before于随后对这个锁的加锁
3.volatile变量规则：对一个volatile域的写，happens-before于任意后续对这个volatile域的读
4.传递性：如果A happens-before B，且B happens-before C，那么A happens-before C
5.start规则：如果线程A执行操作ThreadB.start()（启动线程B），那么A线程的ThreadB.start()操作happens-before于线程B中的任意操作
6.join规则：如果线程A执行操作ThreadB.join()并成功返回，那么线程B中的任意操作happens-before于线程A从ThreadB.join()操作成功返回。
参考链接：https://www.cnblogs.com/chenssy/p/6393321.html
4：synchronized
偷个懒，放个链接（PS：这个博主写的真好）
https://www.cnblogs.com/mingyao123/p/7424911.html
回头再回顾下多线程那本书
5：final
final总体表达不可变的语义，final的四种用法：
- 修饰数据：包括成员变量和局部变量。该变量只能被赋值一次且它的值无法被改变。对于成员变量来说，只能在声明处或者构造方法中赋值
- 修饰方法参数：表示这个参数在方法生命周期中不能被重新赋值
- 修饰方法：表示该方法无法被重写；
- 修饰类：表示该类无法被继承；
6：static
- 修饰属性，使其成为类属性，此类的所有对象共享此属性；
- 修饰方法，使其成为类方法，调用时可直接使用类名.方法名来调用，就不用再创建对象；
- 修饰代码块，一般用于类成员的初始化；
- 静态引入(import static)，通过静态引入的静态属性或静态方法，可以直接用名称引用，不用使用类名.的形式；
7：const
const是Java中的预留关键字，类似预留关键字还有goto。目前暂时没用。C语言中const类似final。
