.NetCore从零开始使用Skywalking分布式追踪系统

将本文从0开始搭建两个webapi项目，使用Skywalking来追踪他们之间的调用关系及响应时间。开发环境为VisualStudio2019

1：安装Skywalking,可参考：https://www.cnblogs.com/sunyuliang/p/11422576.html，本列中搭建好后的Skywalking服务器地址为：192.168.150.134

2：打开VS创建一个demo1的webapi项目。

2.1：为项目添加NuGet程序包SkyAPM.Agent.AspNetCore的引用

　　2.2，在项目根目录添加skyapm.json文件，并添加下以内容，其中的Servers结点的IP地址根据实际情况换成自己的服务器IP

{
  "SkyWalking": {
    "ServiceName": "Demo01",
    "Namespace": "",
    "HeaderVersions": [
      "sw6"
    ],
    "Sampling": {
      "SamplePer3Secs": -1,
      "Percentage": -1.0
    },
    "Logging": {
      "Level": "Debug",
      "FilePath": "logs/skyapm-{Date}.log"
    },
    "Transport": {
      "Interval": 3000,
      "ProtocolVersion": "v6",
      "QueueSize": 30000,
      "BatchSize": 3000,
      "gRPC": {
        "Servers": "192.168.150.134:11800",
        "Timeout": 10000,
        "ConnectTimeout": 10000,
        "ReportTimeout": 600000
      }
    }
  }
}

　　2.3: 修改skyapm.json文件的属性”复制到输入目录“ 修改为 ”如果较新则复制”

2.4:展开项目的Properties，打开launchSettings.json文件，在其中的环境变量中加入 "SKYWALKING__SERVICENAME": "asp-net-core-frontend"

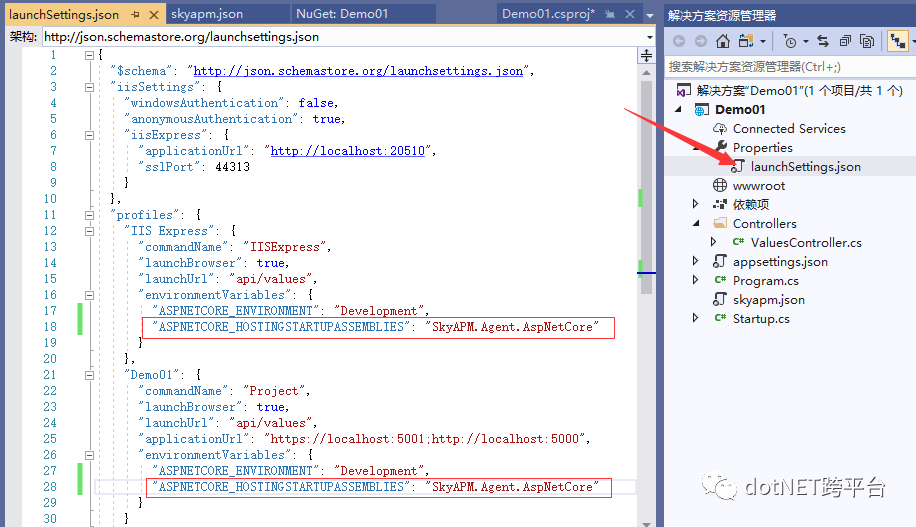
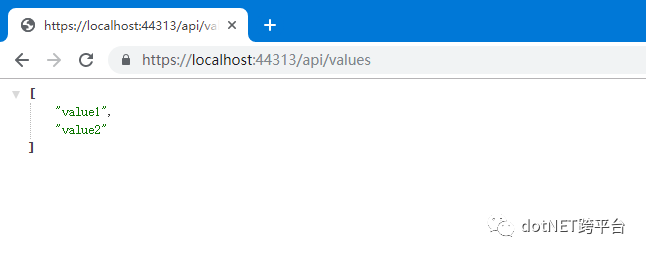
640?wx_fmt=png

　　2.5：到目前skywalking就已经成功引入到系统中了。接下来我们来验证一下是否正常，直接Ctrl+F5启动项目，访问https://localhost:44313/api/values

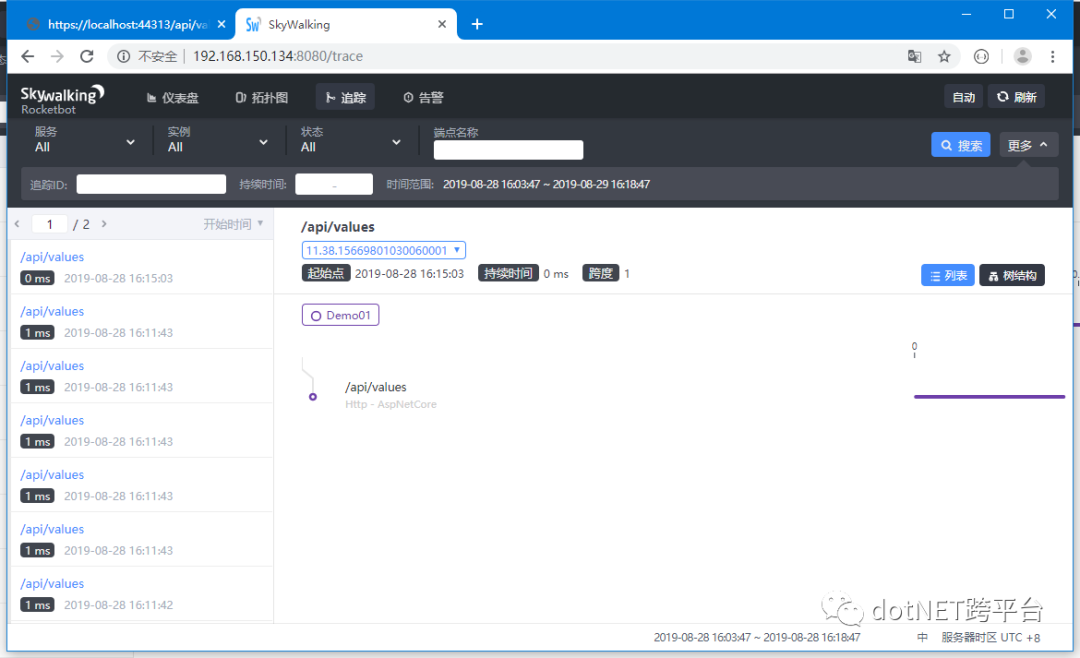
　　　　　　　 640?wx_fmt=png

　　2.6：访问Skywalking管理后台(记得替换一下IP)http://192.168.150.134:8080/trace 。手动选一下时间范围，结束时间选明天(选当时时间会搜索不到数据，不知道是时区还是skywalking的bug)，点击搜索。可以看到本次访问的追踪信息已经同步到了Skywalking中。

　　　　 640?wx_fmt=png

以上单个系统的追踪就完成了，接下来我们再创建一个项目，步骤和第2步基本一样，看看多系统的追踪，这个才是Skywalking的价值所在。

3：另外再打开一个VS创建一个demo02的webapi项目。

3.1：为项目添加NuGet程序包SkyAPM.Agent.AspNetCore的引用

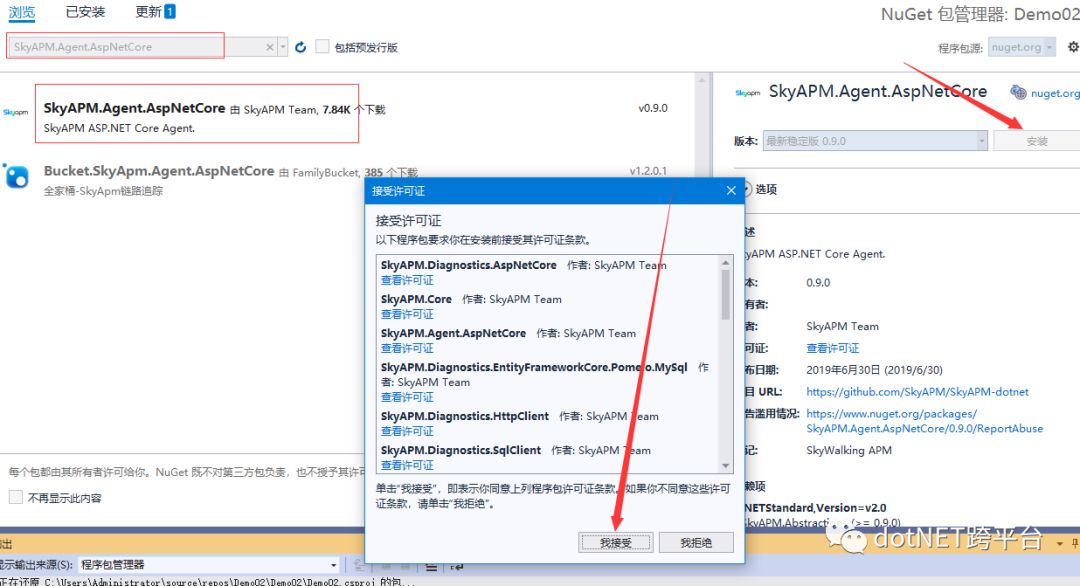
640?wx_fmt=png

　　3.2，在项目根目录添加skyapm.json文件，并添加下以内容，其中的Servers结点的IP地址根据实际情况换成自己的服务器IP。其中ServiceName结点设置为：Demo02

{
  "SkyWalking": {
    "ServiceName": "Demo02",
    "Namespace": "",
    "HeaderVersions": [
      "sw6"
    ],
    "Sampling": {
      "SamplePer3Secs": -1,
      "Percentage": -1.0
    },
    "Logging": {
      "Level": "Debug",
      "FilePath": "logs/skyapm-{Date}.log"
    },
    "Transport": {
      "Interval": 3000,
      "ProtocolVersion": "v6",
      "QueueSize": 30000,
      "BatchSize": 3000,
      "gRPC": {
        "Servers": "192.168.150.134:11800",
        "Timeout": 10000,
        "ConnectTimeout": 10000,
        "ReportTimeout": 600000
      }
    }
  }
}

　　3.3: 修改skyapm.json文件的属性”复制到输入目录“ 修改为 ”如果较新则复制”

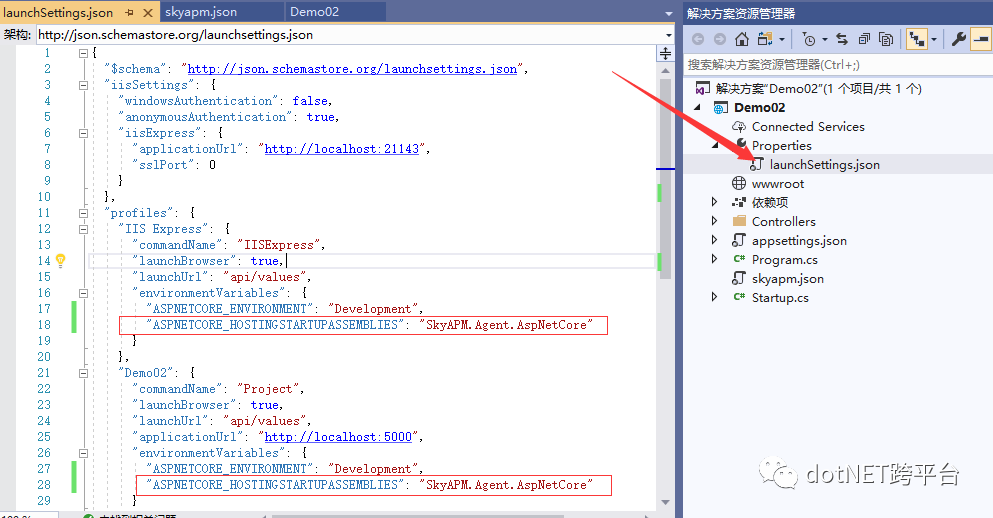
3.4:展开项目的Properties，打开launchSettings.json文件，在其中的环境变量中加入 "ASPNETCORE_HOSTINGSTARTUPASSEMBLIES": "SkyAPM.Agent.AspNetCore"

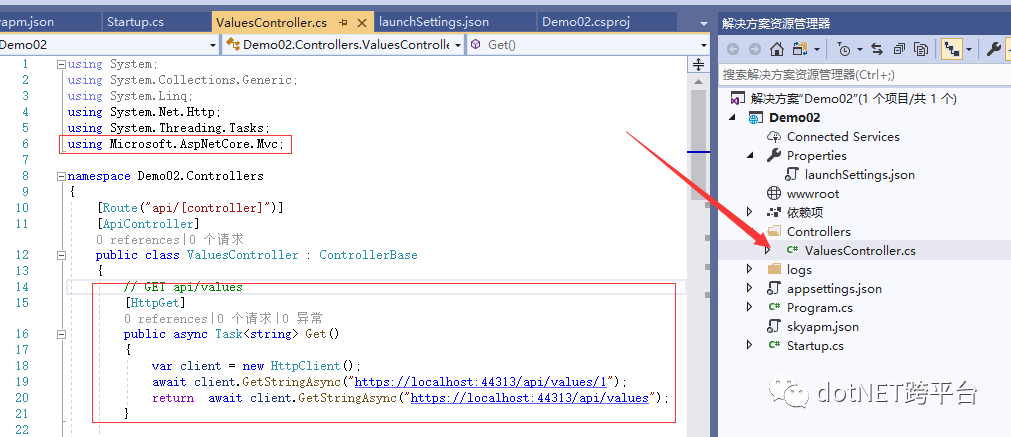
640?wx_fmt=png

　　3.5：在将ValuesController.cs中不加引用： using Microsoft.AspNetCore.Mvc; ，通过HttpClient依次调用Demo01的两个方法，里面的https://localhost:44313对应为我们的Demo01项目。具体Get方法代码如下：

        // GET api/values
        [HttpGet]
public async Task<string> Get()
        {
var client = new HttpClient();
await client.GetStringAsync("https://localhost:44313/api/values/1");
return  await client.GetStringAsync("https://localhost:44313/api/values");
        }

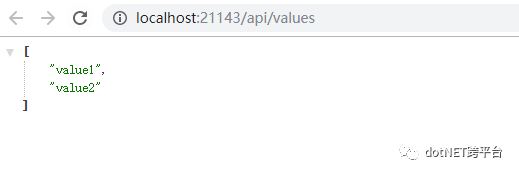
640?wx_fmt=png

3.6：Ctrl+F5启动项目，访问http://localhost:21143/api/values

640?wx_fmt=png

　　3.7：访问Skywalking管理后台(记得替换一下IP)http://192.168.150.134:8080/trace 。手动选一下时间范围，结束时间选明天(选当时时间会搜索不到数据，不知道是时区还是skywalking的bug)，点击搜索。可以看到本次访问两系统单的调用关系图已经同步到了Skywalking中

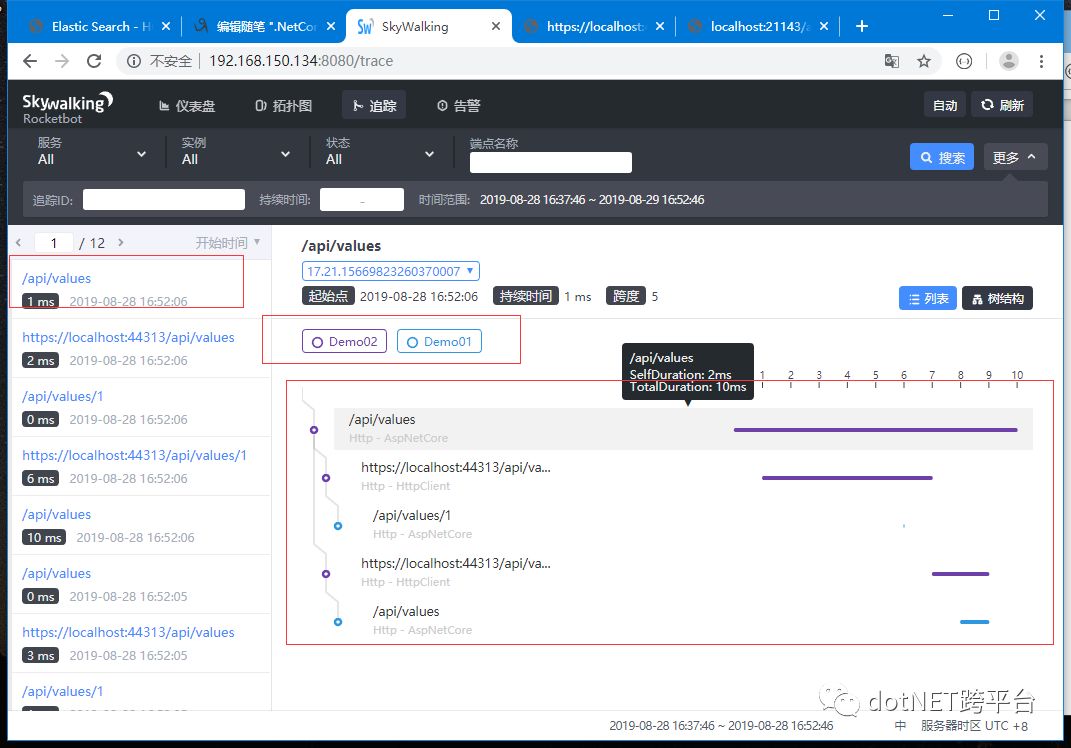
640?wx_fmt=png