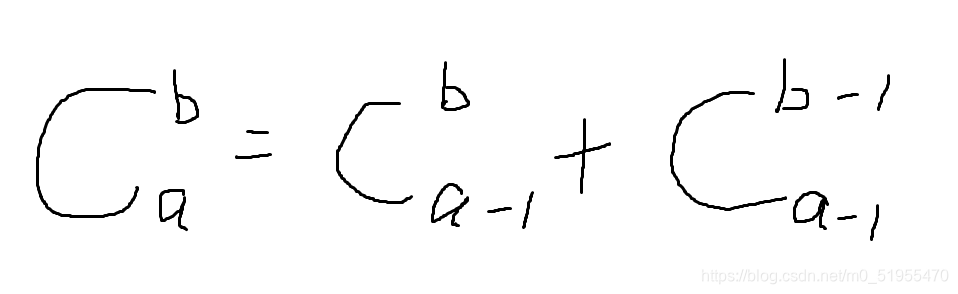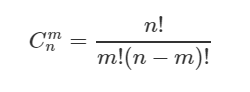哈希表存储结构:
1.开放寻址法
2.拉链法
哈希表的主要作用:
把一个较大(0-10^9 )的数据映射到较小(0-N(N一般为10^5 到 10^6))的数据
哈希函数:可以把一个从-10^19 到10^19 的中的一个数映射到0-10^5之间的一个数
1.哈希函数怎么写?
一般情况下,直接取模,x%10^5,我们一般模的数,一般取为质数,并且离2的整次幂尽可能的远,这样取,冲突的概率最小
2.冲突:把2个不一样的数映射成同一个数怎么办?
我们可以用开放寻址法或者拉链法来解决这个问题
首先我们先定义哈希函数:h(a) = b,指我们将a映射成b
这里我们只介绍拉链法。
拉链法:
参考文献:
图示算法
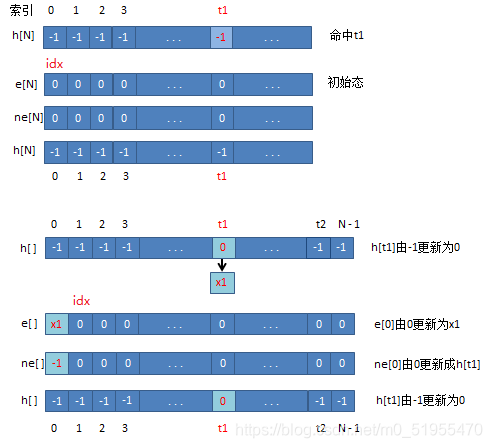
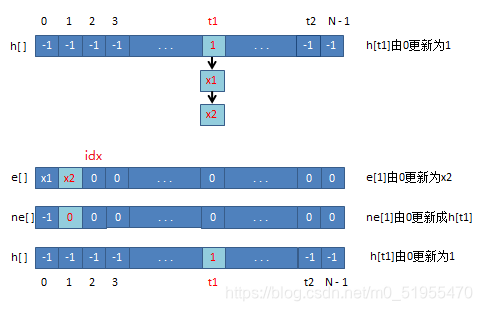

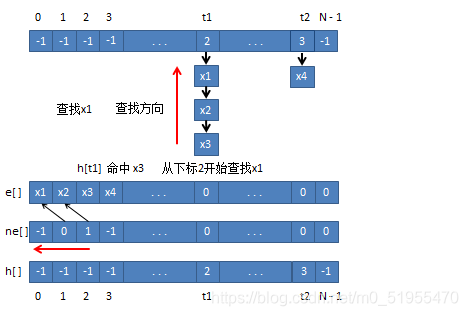
举个例子:
维护一个集合,支持如下几种操作:
“I x”,插入一个数x;
“Q x”,询问数x是否在集合中出现过;
现在要进行N次操作,对于每个询问操作输出对应的结果。
输入格式
第一行包含整数N,表示操作数量。
接下来N行,每行包含一个操作指令,操作指令为”I x”,”Q x”中的一种。
输出格式
对于每个询问指令“Q x”,输出一个询问结果,如果x在集合中出现过,则输出“Yes”,否则输出“No”。
每个结果占一行。
数据范围
1≤N≤105
−109≤x≤109
输入样例:
5
I 1
I 2
I 3
Q 2
Q 5
输出样例:
Yes
No
代码如下:
#include <iostream>
#include <cstring>
using namespace std;
const int N = 1e5+3;
int h[N],e[N],ne[N],idx;
void Insert(int x)
{int t = (x%N+N)%N;e[idx] = x;ne[idx] = h[t];h[t] = idx++;}bool find(int x)
{int t = (x%N+N)%N;for (int i = h[t];i!=-1;i = ne[i]){if (e[i]==x){return true;}}return false;
}int main()
{int cnt;cin>>cnt;memset(h,-1,sizeof(h));while(cnt--){string a;int b;cin>>a>>b;if (a[0]=='I') Insert(b);else{if (find(b)){cout<<"Yes"<<endl;}else{cout<<"No"<<endl;}}}return 0;
}