【问题描述】
从一个 5 x 5 的方格矩阵的左上角出发，沿着方格的边走，满足以下条件的路线有多少种？
总长度不超过 12；
最后回到左上角；
路线不自交；
不走出 5 x 5 的方格矩阵范围之外。
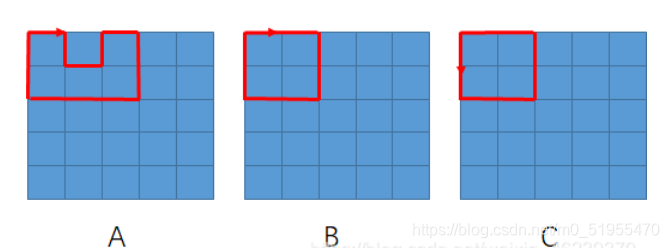
如下图所示，ABC 是三种合法的路线。注意 B 和 C 由于方向不同，所以视为不同的路线。
答案提交
这是一道结果填空的题，你只需要算出结果后提交即可。
本题的结果为一个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。
下面的代码为什么错呢？？？
#include <iostream>
using namespace std;int dx[] = {0, 0, 1, -1}, dy[] = {1, -1, 0, 0};
const int N = 7;
bool vis[N][N];
int ans;void dfs(int x, int y, int u) {if (u > 12)return ;if (x == 0 && y == 0 && u != 0) {ans++;return ;}for (int i = 0; i < 4; i++) {int xx = x + dx[i], yy = y + dy[i];if (xx < 0 || xx > 5 || yy < 0 || yy > 5 || vis[xx][yy])continue;vis[xx][yy] = true;dfs(xx, yy, u + 1);vis[xx][yy] = false;}
}int main() {dfs(0, 0, 0);cout << ans << endl;return 0;
}
因为条件:
u != 0
这个条件有种情况没考虑到，这也是这题的坑点，当在起点的时候，起点我们是没有标记的，然后标记下面那一点，然后往下走，然后会发现上面那一点，也就是起点，没有标记，然后就可以走，导致其实这种情况路线自交了，因为起点在左上角，所以可以往下和往右，所以算出来结果会多2种情况，我们要把条件改成:
u > 2
代码如下：
#include <iostream>
using namespace std;int dx[] = {0, 0, 1, -1}, dy[] = {1, -1, 0, 0};
const int N = 7;
bool vis[N][N];
int ans;void dfs(int x, int y, int u) {if (u > 12)return ;if (x == 0 && y == 0 && u > 2) {ans++;return ;}for (int i = 0; i < 4; i++) {int xx = x + dx[i], yy = y + dy[i];if (xx < 0 || xx > 5 || yy < 0 || yy > 5 || vis[xx][yy])continue;vis[xx][yy] = true;dfs(xx, yy, u + 1);vis[xx][yy] = false;}
}int main() {dfs(0, 0, 0);cout << ans << endl;return 0;
}
)
