面试题8：旋转数组的最小数字
题目：把一个数组最开始的若干个元素搬到数组的末尾，我们称之为数组的旋转。输入一个递增排序的数组的一个旋转，输出旋转数组的最小元素。例如数组{3,4,5,1,2}为{1,2,3,4,5}的一个旋转，该数组的最小值为1。

在数组{3,4,5,1,2}中查找最小值的过程:

#include <iostream>
using namespace std;int Min(int *numbers, int length)
{if (numbers == nullptr || length <= 0) throw new exception("Invalid parameters");int idx1 = 0;int idx2 = length - 1;int idxmin = idx1;while (numbers[idx1] >= numbers[idx2]){if (idx2 - idx1 == 1){idxmin = idx2;break;}idxmin = (idx1 + idx2) / 2;if (numbers[idxmin] >= numbers[idx1]) idx1 = idxmin;else if (numbers[idxmin] <= numbers[idx2]) idx2 = idxmin;}return numbers[idxmin];
}

前面我们提到在旋转数组中，由于是把递增排序数组前面的若干个数字搬到数组的后面，因此第一个数字总是大于或者等于最后一个数字。
但按照定义还有一个特例：如果把排序数组的前面的 0 个元素搬到最后面，即排序数组本身，这仍然是数组的一个旋转，我们的代码需要支持这种情况。
此时，数组中的第一个数字就是最小的数字，可以直接返回。
这就是在上面的代码中，把indexMid初始化为index1的原因。
一旦发现数组中第一个数字小于最后一个数字，表明该数组是排序的，就可以直接返回第一个数字了。

上述代码是否就完美了呢？面试官会告诉我们其实不然。
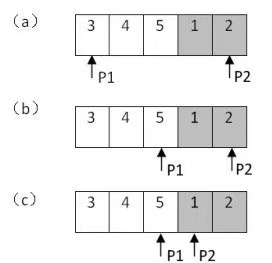
他将提示我们再仔细分析下标为index1和index2（index1和index2分别和图中P1和P2相对应）的两个数相同的情况。

在前面的代码中，当这两个数相同，并且它们中间的数字（即indexMid指向的数字）也相同时，我们把indexMid赋值给了 index1，也就是认为此时最小的数字位于中间数字的后面。

是不是一定这样？

我们再来看一个例子。

数组{1,0,1,1,1}和数组{1,1,1,0,1}都可以看成是递增排序数组{0,1,1,1,1}的旋转，图2.11分别画出它们由最小数字分隔开的两个子数组。

图2.11 数组{0,1,1,1,1}的两个旋转{1,0,1,1,1}和{1,1,1,0,1}

注：在这两个数组中，第一个数字、最后一个数字和中间数字都是1，我们无法确定中间的数字 1 属于第一个递增子数组还是属于第二个递增子数组。
第二个子数组用灰色背景表示。

在这两种情况中，第一个指针和第二个指针指向的数字都是1，并且两个指针中间的数字也是1，这3个数字相同。
在第一种情况中，中间数字（下标为2）位于后面的子数组；
在第二种情况中，中间数字（下标为2）位于前面的子数组中。

因此，当两个指针指向的数字及它们中间的数字三者相同的时候，我们无法判断中间的数字是位于前面的子数组中还是后面的子数组中，也就无法移动两个指针来缩小查找的范围。

此时，我们不得不采用顺序查找的方法。

在把问题分析清楚形成清晰的思路之后，我们就可以把前面的代码修改为：

#include <iostream>
using namespace std;int Min(int *numbers, int length)
{if (numbers == nullptr || length <= 0) throw new exception("Invalid parameters");int idx1 = 0;int idx2 = length - 1;int idxmin = idx1;while (numbers[idx1] >= numbers[idx2]){if (idx2 - idx1 == 1){idxmin = idx2;break;}idxmin = (idx1 + idx2) / 2;if (numbers[idx1] == numbers[idx2] && numbers[idxmin] == numbers[idx1]) return MinInOrder(numbers, idx1, idx2);if (numbers[idxmin] >= numbers[idx1]) idx1 = idxmin;else if (numbers[idxmin] <= numbers[idx2]) idx2 = idxmin;}return numbers[idxmin];
}int MinInOrder(int *numbers, int idx1, int idx2)
{int res = numbers[idx1];for (int i = idx1 + 1; i <= idx2; i++){if (res > numbers[i]) res = numbers[i];}return res;
}

测试用例：
● 功能测试（输入的数组是升序排序数组的一个旋转，数组中有重复数字或者没有重复数字）。
● 边界值测试（输入的数组是一个升序排序的数组、只包含一个数字的数组）。
● 特殊输入测试（输入NULL指针）。
本题考点：
● 考查对二分查找的理解。本题变换了二分查找的条件，输入的数组不是排序的，而是排序数组的一个旋转。这要求我们对二分查找的过程有深刻的理解。
● 考查沟通学习能力。本题面试官提出了一个新的概念：数组的旋转。我们要在很短时间内学习理解这个新概念。在面试过程中如果面试官提出新的概念，我们可以主动和面试官沟通，多问几个问题把概念弄清楚。
● 考查思维的全面性。排序数组本身是数组旋转的一个特例。另外，我们要考虑到数组中有相同数字的特例。如果不能很好地处理这些特例，就很难写出让面试官满意的完美代码。