面试题9：斐波那契数列
题目一：写一个函数，输入n，求斐波那契（Fibonacci）数列的第n项。斐波那契数列的定义如下：

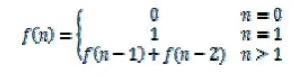
❖ 效率很低的解法，挑剔的面试官不会喜欢

代码如下:

long long fib(unsigned int n)
{if (n <= 0) return 0;if (n == 1) return 1;return fib(n - 1) + fib(n - 2);
}

❖ 面试官期待的实用解法

其实改进的方法并不复杂。上述递归代码之所以慢是因为重复的计算太多，我们只要想办法避免重复计算就行了。
比如我们可以把已经得到的数列中间项保存起来，如果下次需要计算的时候我们先查找一下，如果前面已经计算过就不用再重复计算了。

更简单的办法是从下往上计算，首先根据f（0）和f（1）算出f（2），再根据f（1）和f（2）算出f（3）……依此类推就可以算出第n 项了。很容易理解，这种思路的时间复杂度是O（n）。

实现代码如下：

#include <iostream>
using namespace std;
typedef long long LL;LL fib(unsigned int n)
{int res[2] = { 0,1 };if (n < 2) return res[n];LL fibminone = 1;LL fibmintwo = 0;LL fibN = 0;for (unsigned int i = 2; i <= n; i++){fibN = fibminone + fibmintwo;fibmintwo = fibminone;fibminone = fibN;}return fibN;
}

测试用例：
● 功能测试（如输入3、5、10等）。
● 边界值测试（如输入0、1、2）。
● 性能测试（输入较大的数字，如40、50、100等）。
本题考点：
● 考查对递归、循环的理解及编码能力。
● 考查对时间复杂度的分析能力。
● 如果面试官采用的是青蛙跳台阶的问题，那同时还在考查应聘者的数学建模能力。