数据结构与算法--面试必问AVL树原理及实现

数据结构与算法–AVL树原理及实现

  • AVL（Adelson-Velskii 和landis）树是带有平衡条件的二叉查找树，这个平衡条件必须容易实现，并且保证树的深度必须是O(logN)。因此我们让一棵AVL树中每个节点的左子树和右子树的高度最多相差1（空树高度定义-1）如下图，左边是AVL树，右边不是AVL树。
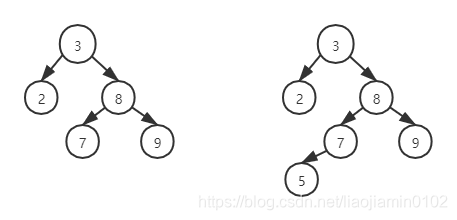
  • 在这里插入图片描述
  • 左图中3 节点左子树高度0，右子树高度1，相差不超过1。
  • 右图中节点3，左子树盖度0，右子树高度2，相差超过1，不满足AVL数要求。
  • 我们可以在每一个节点中保留高度信息，那我们可以推算出如下 高度h 与节点之间关系的公式
    • 在高度h的AVL树中，最少节点数S(h)由S(h)=S(h-1)+S(h-2)+1标识
    • 对于h，S(h)=1; h=1, S(h)=2，明显函数S(h)与斐波那契数列密切相关，由此我们可以推算出AVL数的高度的界限1.44log(N+2)-1.328。
insert分析

  • 经过如上高度，限制条件分析，我们可以认为，AVL树操作都可以以时间O(logN)执行。当插入操作时候，我们需要更通向根节点路径上那些节点的所有平衡信息，而插入操作比较棘手的地方子阿姨，一个插入节点可能破坏AVL的平衡性。

    • 上图中左图插入数据5，变成右图，平衡性改变，不符合AVL树特性

  • 因此我们需要考虑在insert之后恢复平衡性，这种操作总可以通过树进行简单的修正做到，我们成为旋转。

  • 我们将insert后必须重新平衡的节点记录为a。由于任意节点最多两个儿子，因此出现高度不平衡需要a的左右子树的高度相差2，容易推出如下四种情况：

    • 对a的左子树的左子树进行一次insert
    • 对a的左子树的右子树进行一次insert
    • 对a的右子树的左子树进行一次insert
    • 对a的右子树的右子树进行一次insert

  • 上面四点中 第一点与第四点镜像对称，第二点和第三点镜像对称，理论上我们只需要实现两种就可以同样的实现方法得出对称的方法。

  • 第一种情况发生在外侧情况（左左或者右右），该情况通过一次单旋转可以完成跳转。

  • 第二中情况发生在内部(左右或者右左)，这种情况需要复杂一些的双旋转。

单旋转

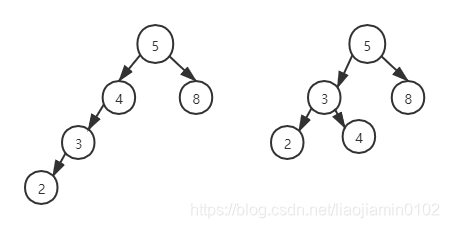
在这里插入图片描述

  • 如上图左图中的树节点4不满足AVL树，因为他的左子树的深度比右子树深2层，改图中描述的情况是第一点1中描述的情况。在插入2 节点之后，原来满足AVL数的性质遭到了破坏，子树 3多出了一层我们需要调整节点然他在平衡。
  • 我们将3节点上移，并且将4节点下移，得到右图中所示的新的树满足AVL特性
  • 我们可以形象的将树看成是柔软的，抓住3 节点向上提在重力的作用下3节点变成了新的根节点（子树的根）。由于二叉查找树的特性，4>3，
    • 所以4节点变成了3节点的右节点。
    • 如果3 有右节点x，那么3的右节点应该变成4的左节点，因为x>3 并且x<4
    • 2的左右节点不变，4的右节点不变
      -我们在来插入一个数据1 ，得出如下结果：

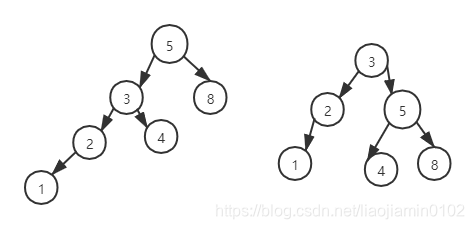
在这里插入图片描述

  • 如上左图我们插入1 后，破坏了5 根节点的平衡性，5节点的左子树深度3， 右子树深度1，超过2，因此我们应该在3 节点处进行如上步骤的操作得到最终的AVL数右图：
    • 3节点编程根节点，5节点编程3的右节点
    • 3的右节点交给5的左节点
    • 其他节点不变
双旋转

  • 上面案例中的算法小时，在下图找那个是无效的：
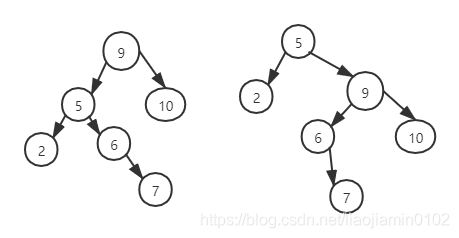
    在这里插入图片描述

  • 如上左图到右图的变化，9节点在插入 7 节点后，时序平衡性，我们在5与9节点之间作旋转，按上面描述的算法，得到右图，还是非AVL数

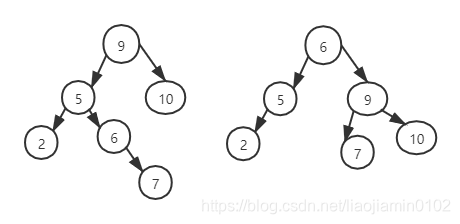
  • 我们通过如上的实验得出5 和9 之间的旋转无法解决问题。也就是5， 9 作为根都无法得到一个平衡树，那么只能由6 节点作为跟节点

  • 如此的话，节点的顺序就一目了然了： 5节点是6左子树，9 是右子树，7 变为9 的左子树。得到如下结果：

在这里插入图片描述

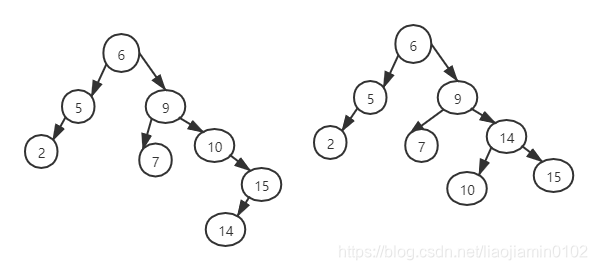
  • 我们继续接着上面的案例插入 15， 14，13。插入13容易，因为他不会破坏节点的平衡性，但是插入12 之后硬气10 节点的高度不平衡，这个属于上面描述的情况3 的案例：需要通过一次右-左双旋来解决这个问题。在这里插入图片描述
  • 如上左图中，右-左旋流程：
    • 我们先在15 节点和14节点之间做一次右旋转，我们在做这次右旋转流程时候，假设14节点左节点还有一个节点是我们假设的虚拟节点
    • 那么此时15 节点就满足上述情况中的第一点左 左描述情况，那么我们用右旋得到如下图情况：
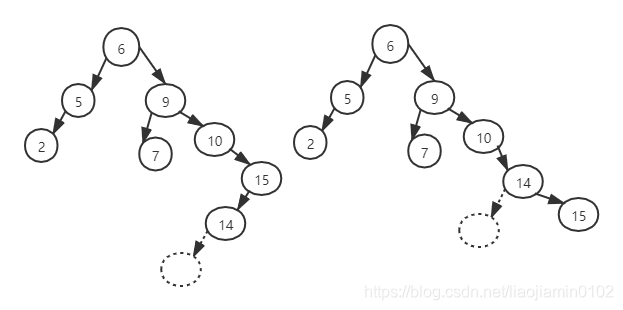
      在这里插入图片描述
  • 如上图我们完成了第一次右边选择，图中虚线表示虚拟节点不存在
  • 那么我们再看此时10 节点也是不符合平衡性质，而且恰好此时满足第四点情况描述的右右的描述
  • 那么我们按照之前的算法描述需要对10，14 节点之间进行左旋得到如下结果

在这里插入图片描述

总结
  • 至此我们对上面两种旋转做一个总结，为了将项X的一个新节点插入到一个AVL树中，
    • 我们递归的将X插入到T数对应的子树位置，记录改子树为T_lr
    • 如果T_lr的高度不变那么插入完成
    • 如果T中出现高度不平衡，则根据X以及T和T_lr中项做适当的单旋或者双旋来更新这些高度
    • 解决旋转之后其他节点的归属问题
  • 经过如上分析，我们给出以下实现（二叉查找树上一节已经实现，在此基础上进行修改）：
算法实现
  • 节点定义，还是和上一节二叉查找树中类似，只不过我们在节点中需要维护一个高度信息，并且修改了comparable方法。如下实现：
/*** 二叉树节点对象定义** @author liaojiamin* @Date:Created in 15:24 2020/12/11*/
public class BinaryNode implements Comparable {private Object element;private BinaryNode left;private BinaryNode right;/*** 树高度*/private int height;private int count;public BinaryNode(Object element, BinaryNode left, BinaryNode right) {this.element = element;this.left = left;this.right = right;this.count = 1;this.height = 0;}public int getHeight() {return height;}public void setHeight(int height) {this.height = height;}public Object getElement() {return element;}public void setElement(Object element) {this.element = element;}public BinaryNode getLeft() {return left;}public void setLeft(BinaryNode left) {this.left = left;}public BinaryNode getRight() {return right;}public void setRight(BinaryNode right) {this.right = right;}public int getCount() {return count;}public void setCount(int count) {this.count = count;}@Overridepublic int compareTo(Object o) {if (o == null) {return 1;}int flag;if (o instanceof Integer) {int myElement = (int) this.element - (int) o;flag = myElement > 0 ? 1 : myElement == 0 ? 0 : -1;} else {flag = this.element.toString().compareTo(o.toString());}if (flag == 0) {return 0;} else if (flag > 0) {return 1;} else {return -1;}}
}
  • 单左旋，单右旋代码实现：
/*** 左单旋一次* */private BinaryNode rotateWithLeftChild(BinaryNode k2){BinaryNode k1 = k2.getLeft();k2.setLeft(k1.getRight());k1.setRight(k2);k2.setHeight(Math.max(height(k2.getLeft()), height(k2.getRight())) + 1);k1.setHeight(Math.max(height(k1.getLeft()), height(k2)) + 1);return k1;}/*** 右单旋一次* */private BinaryNode rotateWithRightChild(BinaryNode k2){BinaryNode k1 = k2.getRight();k2.setRight(k1.getLeft());k1.setLeft(k2);k2.setHeight(Math.max(height(k2.getLeft()), height(k2.getRight())) + 1);k1.setHeight(Math.max(height(k2), height(k1.getRight())) + 1);return k1;}
  • 如上代码实现，用下图说明，6节点因为3 的插入破坏平衡性
    • 我们在6节点和5节点之前进行选择
    • 5节点成为新根节点
    • 6 节点成为5节点的右节点
    • 5节点的右节点编程6节点的左节点
    • 和如上左旋流程一样，达到目的

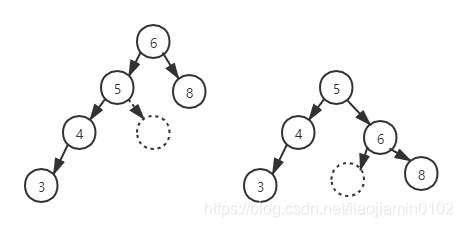
在这里插入图片描述

  • 双左旋，双右旋转实现：
  /*** 右旋转 接左旋转，双旋转* */private BinaryNode doubleWithLeftChild(BinaryNode k3){k3.setLeft(rotateWithRightChild(k3.getLeft()));return rotateWithLeftChild(k3);}/*** 左旋转 接右旋转，双旋转* */private BinaryNode doubleWithRightchild(BinaryNode k3){k3.setRight(rotateWithLeftChild(k3.getRight()));return rotateWithRightChild(k3);}

  • 双旋的情况我们将他看出是两段，两段分别进行单旋操作:

    • 第一步，如下图，有K2节点进行右旋得到右图中树结构
      在这里插入图片描述

  • 第二步，对k3进行左旋

在这里插入图片描述

  • 删除操作，添加操作：添加操作破坏平衡性，之后在纠正，由于二叉查找树的删除比插入更加复杂，英雌AVL删除也同样，我们也可以和insert方法一样，在insert之后在纠正平衡性，这样就可以在二叉查找树的基础上进行很简单的实现：
/*** 插入节点** @author: liaojiamin* @date: 15:48 2020/12/15*/private BinaryNode insert(Object x, BinaryNode t) {if (x == null) {return t;}if (t == null || t.getElement() == null) {t = new BinaryNode(x, null, null);return t;}int flag = t.compareTo(x);if (flag > 0) {t.setLeft(insert(x, t.getLeft()));} else if (flag < 0) {t.setRight(insert(x, t.getRight()));} else {t.setCount(t.getCount() + 1);}return balance(t);}/*** 删除节点** @author: liaojiamin* @date: 15:48 2020/12/15*/private BinaryNode remove(Object x, BinaryNode t) {if (x == null) {return t;}int flag = t.compareTo(x);if (flag > 0) {return remove(x, t.getLeft());} else if (flag < 0) {return remove(x, t.getRight());} else if (t.getLeft() != null && t.getRight() != null) {//找到对应节点，将节点右子树下面最小的值替换当前值BinaryNode min = findMin(t.getRight());t.setElement(min.getElement());//递归删除右子树下最小值remove(min.getElement(), t.getRight());} else {//找到对应节点，但是当前节点只有一个子节点// 递归思想：只考虑最简单情况，当只有当前节点与其左子节点，删除当前节点返回当节点左子节点，右节点同理t = t.getLeft() != null ? t.getLeft() : t.getRight();}return balance(t);}
  • 平衡性纠正方法：
 private static final int MAXBALANCE_HEIGH = 1;/*** 平衡查找二叉树** */public BinaryNode balance(BinaryNode t){if(t == null){return t;}if(height(t.getLeft()) - height(t.getRight()) > MAXBALANCE_HEIGH){if(height(t.getLeft().getLeft()) >= height(t.getLeft().getRight())){t = rotateWithLeftChild(t);}else {t = doubleWithLeftChild(t);}}else if(height(t.getRight()) - height(t.getLeft()) > MAXBALANCE_HEIGH ){if(height(t.getRight().getRight()) >= height(t.getRight().getLeft())){t = rotateWithRightChild(t);}else {t = doubleWithRightchild(t);}}t.setHeight(Math.max(height(t.getLeft()), height(t.getRight())) + 1);return t;}
  • 其他方法：
/*** 按顺序打印节点信息：左中右** @author: liaojiamin* @date: 15:48 2020/12/15*/public void printTree(BinaryNode t) {if (t == null || t.getElement() == null) {return;}printTree(t.getLeft());for (int i = 0; i < t.getCount(); i++) {System.out.print(t.getElement() + " ");}printTree(t.getRight());}/*** 获取树高度* */private int height(BinaryNode t){return t == null ? -1 : t.getHeight();}public void makeEmpty(BinaryNode root) {root = null;}public boolean isEmpty(BinaryNode root) {return root == null;}public static void main(String[] args) {BinaryNode node = new BinaryNode(null, null, null);AvlTree searchTree = new AvlTree();Random random = new Random();for (int i = 0; i < 20; i++) {node = searchTree.insert(random.nextInt(100), node);}System.out.println(searchTree.findMax(node).getElement());System.out.println(searchTree.findMin(node).getElement());searchTree.printTree(node);if(!searchTree.contains(13, node)){node = searchTree.insert(13, node);}System.out.println(searchTree.contains(13, node));node = searchTree.remove(13, node);System.out.println(searchTree.contains(13, node));}/*** 节点元素是否存在** @author: liaojiamin* @date: 15:48 2020/12/15*/private boolean contains(Object x, BinaryNode t) {if (x == null) {return false;}if (t == null) {return false;}int flag = t.compareTo(x);if (flag > 0) {return contains(x, t.getLeft());} else if (flag < 0) {return contains(x, t.getRight());} else {return true;}}/*** 查找最小元素节点** @author: liaojiamin* @date: 15:48 2020/12/15*/private BinaryNode findMin(BinaryNode t) {if (t == null) {return null;}if (t.getLeft() != null) {return findMin(t.getLeft());}return t;}/*** 查找最大元素节点** @author: liaojiamin* @date: 15:48 2020/12/15*/private BinaryNode findMax(BinaryNode t) {if (t == null) {return null;}if (t.getRight() != null) {return findMax(t.getRight());}return t;}

上一篇：数据结构与算法–二叉查找树实现原理
下一篇：数据结构与算法–二叉堆（最大堆，最小堆）实现及原理

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.mzph.cn/news/310478.shtml

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

MySQL8.0新特性

MySQL8.0新特性

在这之前Mysql的版本是5.7&#xff0c;也是目前使用最广泛的一个版本。现在新版本跳过了6和7直接来到了8&#xff0c;那么V6和V7版本去哪里了呢&#xff1f;比较靠谱的说法是v6用作了内部的其他用途而v7的话是因为mysql有个产品叫做clusterdb他有7这个版本&#xff0c;所以这个…
阅读更多...
数据结构与算法--B树原理及实现

数据结构与算法--B树原理及实现

B树 前几篇文中讨论的数据结构我们都是假设所有的数据都存储在计算机的主存中。可说总要那么海量的数据需要通过个中数据结构去存储&#xff0c;我们不可能有这么多内存区存放这些数据。那么意味着我们需要将他们放磁盘。所以这个时候范问时间复杂度O决定了他是否能适合存储磁盘…
阅读更多...
[C++STL]C++实现priority_queue容器适配器

[C++STL]C++实现priority_queue容器适配器

代码如下: #pragma once #include <iostream> #include <vector> using namespace std;template<typename T> struct Less {bool operator()(const T &a, const T &b){return a < b;} };template<typename T> struct Greater {bool operat…
阅读更多...
为什么要用内插字符串代替string.format

为什么要用内插字符串代替string.format

知道为什么要用内插字符串&#xff0c;只有踩过坑的人才能明白&#xff0c;如果你曾今使用string.format超5个以上占位符&#xff0c;那其中的痛苦我想你肯定是能够共鸣的。一&#xff1a;痛苦经历先上一段曾今写过的一段代码&#xff0c;大家来体会一下&#xff1a;LogHelper.…
阅读更多...
SpringCloud Alibaba 框架下公司架构图

SpringCloud Alibaba 框架下公司架构图

上一篇&#xff1a;Docker容器实战思维 下一篇&#xff1a;分布式事务理论模型
阅读更多...
C++ 实现堆

C++ 实现堆

代码如下(小根堆): #include <iostream> #include <assert.h> using namespace std;//小根堆,堆排序从大到小排 class Heap { public:Heap():data(nullptr), size(0), capacity(0) {}~Heap(){delete[] data;data nullptr;size 0;capacity 0;}/*void Swap(int *…
阅读更多...
iPhone上运行Linux也要来了

iPhone上运行Linux也要来了

FOSSBRTES 报道称&#xff0c;用户很快将可以通过双启动功能&#xff0c;像在 Android 设备上那样在 iPhone 上运行 Linux。目前&#xff0c;iOS 越狱极客、开发人员 Raffaele 以及 mcg29 已在其 Github 页面上发布了详细说明&#xff0c;详细介绍了如何双启动 64 位 iOS 设备。…
阅读更多...
数据结构与算法--图论，最短路算法，拓扑排序算法

数据结构与算法--图论，最短路算法，拓扑排序算法

图论若干定义 图&#xff08;graph&#xff09;G&#xff08;V,E&#xff09;由定点vertex的集合V&#xff0c; 和边edge的集合E组成。每一条边都是一个点对点&#xff08;v&#xff0c;w&#xff09;&#xff0c;其中 v,w 属于V集合的子集 如果点对点 是有序的&#xff0c;那…
阅读更多...
谁说.NET不适合搞大数据、机器学习和人工智能

谁说.NET不适合搞大数据、机器学习和人工智能

SciSharp StackSciSharp STACK: https://scisharp.github.io/SciSharp/基于.NET的开源生态系统&#xff0c;用于数据科学、机器学习和AI。SciSharp将所有主要的ML/AI框架从Python引入.NET.特点为.NET开发者.NET开发者使用他们所了解和喜爱的工具可以最高效的工作。我们的使命是…
阅读更多...
C++ 泛型编程 实现红黑树RBTree

C++ 泛型编程 实现红黑树RBTree

代码如下: #include <iostream> #include <ctime> using namespace std;enum COLOR {BLACK,RED };template<typename T> struct RBTreeNode {RBTreeNode<T> * _parent;RBTreeNode<T> * _left;RBTreeNode<T> * _right;T _val;COLOR _color…
阅读更多...
数据结构与算法--图论-深度优先搜索及其应用

数据结构与算法--图论-深度优先搜索及其应用

深度优先搜索 深度优先搜索&#xff08;depth-first search&#xff09; 是对先序遍历&#xff08;preorder traversal&#xff09;的推广&#xff0c;我们从某个顶点v开始处理v&#xff0c;然后递归的遍历所有与v邻接顶点。如果这个过程是对一棵树进行&#xff0c;那么&#…
阅读更多...
.NET Core技术研究-主机

.NET Core技术研究-主机

前一段时间&#xff0c;和大家分享了 ASP.NET Core技术研究-探秘Host主机启动过程但是没有深入说明主机的设计。今天整理了一下主机的一些知识&#xff0c;结合先前的博文&#xff0c;完整地介绍一下.NET Core的主机的设计和构建启动过程。一、什么是主机主机是一个封装了应用资…
阅读更多...
数据结构与算法--贪婪算法

数据结构与算法--贪婪算法

贪婪算法 贪婪算法分阶段地工作。在每个阶段&#xff0c;可以认为所做决定是最好的&#xff0c;而不考虑将来的后果。通常这意味着选择的是某个局部最优。这种“当前能获得的最优就拿”的策略是这类算法的名字来源。当算法终止时候&#xff0c;我们希望的到累积的局部最优解就…
阅读更多...
[C++STL]C++ 实现map容器和set容器

[C++STL]C++ 实现map容器和set容器

代码如下: #pragma once #include <iostream> using namespace std;enum COLOR {BLACK, RED };template<class V>//迭代器声明&#xff0c;定义在后面 struct RBTreeIterator;template<typename V> struct RBTreeNode {RBTreeNode<V> * _parent;RBTre…
阅读更多...
多角度让你彻底明白yield语法糖的用法和原理及在C#函数式编程中的作用

多角度让你彻底明白yield语法糖的用法和原理及在C#函数式编程中的作用

如果大家读过dapper源码&#xff0c;你会发现这内部有很多方法都用到了yield关键词&#xff0c;那yield到底是用来干嘛的&#xff0c;能不能拿掉&#xff0c;拿掉与不拿掉有多大的差别&#xff0c;首先上一段dapper中精简后的Query方法&#xff0c;先让大家眼见为实。private s…
阅读更多...
C++泛型编程实现哈希表(闭散列---线性探测)

C++泛型编程实现哈希表(闭散列---线性探测)

代码如下: #include <iostream> #include <vector> using namespace std;enum STATE {EXIST,DELETE,EMPTY };template<typename K,typename V> struct HashNode {pair<K, V> _kv;STATE _state EMPTY; };template<typename K,typename V> class…
阅读更多...
哪种开源许可证最适合商业化？

哪种开源许可证最适合商业化？

选择最佳开源许可证是为新项目所做的最重要的决定之一。大多数开发者会选用 MIT、BSD 或 Apache 等流行的宽松许可证&#xff08;permissive license&#xff09;。对于商业项目而言&#xff0c;这种选择不错&#xff0c;因为这能减少用户对项目的抵触情绪。当应用于开源项目时…
阅读更多...
C++泛型编程实现哈希表(开散列法)

C++泛型编程实现哈希表(开散列法)

代码如下: #include <iostream> #include <vector> using namespace std;template<typename K> struct HashNode {typedef HashNode<K> Node;K _val;Node * _next;HashNode(const K & val):_val(val),_next(nullptr){} };template<typename K&…
阅读更多...
数据结构与算法--分治算法-最大子序列和问题

数据结构与算法--分治算法-最大子序列和问题

分治算法 用于设计算法的一种常用技巧–分治算法&#xff08;divide and conquer&#xff09;。分治算法由两部分组成&#xff1a; 分(divide)&#xff1a;递归然后借机较小的问题&#xff08;基础情况除外&#xff09;治(conquer)&#xff1a;然后从子问题的解构建原问题的解…
阅读更多...
请把我不会，换成我可以学

请把我不会，换成我可以学

点击蓝字关注&#xff0c;回复“职场进阶”获取职场进阶精品资料一份有位读者跟我说起自己的烦恼&#xff1a;“我到公司已经接近四年了&#xff0c;领导经常让我做一些岗位职责以外的事情。这些东西我都不会&#xff0c;还非让我做。并且一直没有职位上的改变&#xff0c;我怎…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023