概率论与数理统计练习题

1.假设检验中，显著性水平$\alpha$ 限制（第一类错误（拒真错误）#）的概率

分析：
（1）．原假设为真时拒绝原假设的概率不超过α
（2）．犯第一类错误的概率不超过α；（第一类错误概率的上界．）

2.设 A,B 为概率不为零两个随机事件，若 P(A| B) = P(A| $\bar{B}$) ，则 A,B 一定（ 独立）

分析：

3. 设总体 X 服从正态分布 N( $\mu$, ${\sigma }^2$) 其中 $\mu$、${\sigma }^2$ 未知，$X_1\dots X_n$ 是总体 X 的一个简单随机样本，则下${\sigma }^2$ 的无偏估计为（ $\frac{1}{n-1}{\sum }_{i=1}^n(X_i-\overline{X}{)}^2$）， $\overline{X}$ 、$S^2$为样本均值和样本方差，则E($\overline{X}$)=($\mu$ ),E($S^2$)=(),$\overline{X}$~(N( $\mu$, $\frac{{\sigma }^2}{n}$)),$\frac{(n-1)S^2}{{\sigma }^2}$~($X^2(n-1)$ ).

分析：

$S^2=\frac{1}{n-1}{\sum }_{i=1}^n(X_i-\overline{X}{)}^2$

$\overline{X}$= $\frac{1}{n}{\sum }_{i=1}^n{X}_i$

则有：1.$\overline{X}$、$S^2$相互独立

2.$\overline{X}$~(N( $\mu$, $\frac{{\sigma }^2}{n}$))

3.$\frac{(n-1)S^2}{{\sigma }^2}$~($X^2(n-1)$ ).

关于正态总体的样本均值与样本方差的重要结论详细

4．设 ( X,Y ) ~ N( ${\mu }_1,{\mu }_2,{\sigma }_1^2,{\sigma }_2^2$,0)则 随机变量X,Y（相互独立（不相关） ）

分析：设二维随机变量 ( X,Y ) ~ N( ${\mu }_1,{\mu }_2,{\sigma }_1^2,{\sigma }_2^2$,ρ)，则X、Y相互独立的充分必要条件是：相关系数ρ=0。

5.已知随机变量 X ~ t(7),则 $X^2$ ~（ F（1,7）)

分析：X~N(0,1) 、Y~$X^2$(n)，且X与Y独立，则统计量：T=$\frac{X}{\sqrt{\frac{Y}{n}}}$,服从自由度为n的t分布，即为T~t(n).
因为n=7;
$X^2$=$T^2$=$\frac{X^2}{\frac{Y}{n}}$=$\frac{X^2/1}{Y/n}$
由F分布：F(m,n)=$\frac{X/m}{Y/n}$
则 $X^2$ ~ F（1,7）

6.设 $X_1、X_2\dots X_5$ 是总体 X ~ N(0,1) 的样本，当 a =($\frac{\sqrt{6}}{3}$)时，$\frac{a(X_1+X_2+X_3)}{\sqrt{X_4+X_5}}$~t(2).

分析：因为 $X_1、X_2\dots X_5$ 是总体 X ~ N(0,1) 的样本，
且$\frac{a(X_1+X_2+X_3)}{\sqrt{X_4+X_5}}$=$\frac{\sqrt{3}a}{\sqrt{2}}$,
为使$\frac{a(X_1+X_2+X_3)}{\sqrt{X_4+X_5}}$~t(2).，
只需$\frac{\sqrt{3}a}{\sqrt{2}}$=1即可，
得 a =$\frac{\sqrt{6}}{3}$

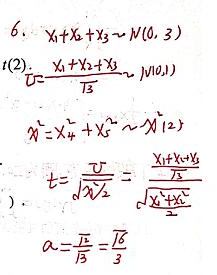
7．已知 D(X ) =1, D(Y) = 3, cov(X ,Y) = 0.6 ，则 D(X - 3Y + 5) = (24.4 ).

分析：因为1、D（C）=0;
2、D（aX+b）=$a^2$D(X);
3、D(X$\pm$Y）=D(X)+D(Y)$\pm$DOV（X,Y)
则D(X - 3Y+5 )
=D(X - 3Y )
=D(X)+9D(Y)-6COV（X,Y)
=1+9$\ast$ 3-0.6$\ast$ 6=24.4

8.随机变量 X ~ N(0,2),Y ~ N(1,3) ， X ,Y 独立，则 Z =2X +Y +3 ~ (N(4,11) )

分析：X ~ N(0,2),Y ~ N(1,3) 且随机变量 X ,Y 独立，故X和Y的任意线性组合是正态分布。即
Z~N（E(Z)，D(Z)），
1.X,Y独立：D(aX$\pm$Y$\pm$b）=$a^2$D(X)+D(Y)
2.E(aX$\pm$Y$\pm$b）=aE(X)$\pm$E(Y)$\pm$b
因为 Z =2X +Y +3 ，
E(Z)=2E(X)+E(Y)+3=20+1+3=4；
D(Z)=4D(X)+D(Y)=42+3=11；
所以Z~N(4,11)；
Z=2X +Y +3 ~N(4,11)

9.随机变量 X ~ P(1),Y ~ P(3)，且 X,Y 相互独立，则随机变量 Z = X +Y ~ (P(4) ) ．

分析：泊松分布具有可加性即Z = X +Y ~P (1+3 )=P(4) ．

10．设 A, B 为随机事件， P(A) = 0.5, P(A- B) = 0.2 ，则 P( $\overline{AB}$) = ( 0.7)．

P(A- B)=P(A)-P(AB)
P(AB)=P(A)-P(A- B)=0.5-0.2=0.3
P( $\overline{AB}$) =1-P(AB)=1-0.3=0.7
扩展资料：
常用概率公式
1、设A、B是互不相容事件（AB=φ），则：P（A∪B）=P（A）+P（B）
推论1：设A1、A2、…、An互不相容，则：P(A1+A2+…+An)=P(A1)+P(A2)+…+P(An)
推论2：设A1、A2、…、An构成完备事件组，则：P(A1+A2+…+An)=1
推论3：为事件A的对立事件。
推论4：若B包含A，则P(B－A)=P(B)－P(A)
推论5（广义加法公式）：对任意两个事件A与B，有P(A∪B)=P(A)+P(B)－P(AB)
2、条件概率：已知事件B出现的条件下A出现的概率，称为条件概率，记作：P(A|B)条件概率计算公式：
当P(A)>0，P(B|A)=P(AB)/P(A)
当P(B)>0，P(A|B)=P(AB)/P(B)
3、乘法公式
P(AB)=P(A)×P(B|A)=P(B)×P(A|B)
推广：P(ABC)=P(A)P(B|A)P(C|AB)

11.设 P(A) =0.3, P(B) = 0.5，则 P(AB) 的最大值为(0.3 ).

分析：由概率加内法公式：
P(AUB)=P(A)+P(B)-P(AB)
得：
P(AB)=P(A)+P(B)-P(AUB)
当P(AUB)最小的时容候P(AB)取到最大值
令AUB=B,那么P(AUB)=P(B)=0.5
P(AB)=P(A)=0.3

12.设某种仪器内装有 4 只同样的电子管，已知电子管的寿命 X 的密度函数为

求：（1）密度函数中的常数 a .

(2)任一电子管在 200 时内损坏的概率.

(3)在开始的 200 时内，4 只电子管无损坏的概率.

答：(1)密度函数f(x)满足∫(-∞,+∞)f(x)dx=1

13,设二维随机变量(X ,Y) 的联合密度函数为

（1）求随机变量 X,Y 的边缘密度函数；

(2)求 Cov（X,Y）；

（3） ${\rho }_{XY}$

分析：（1）边缘密度函数：如果二维随机变量X,Y的分布函数F{x，y}为已知，那么随机变量x，y的分布函数Fx{x}和Fy{y}分别可由F{x，y}求得。则Fx{x}和Fy{y}为分布函数F{x，y}的边缘分布函数。
　
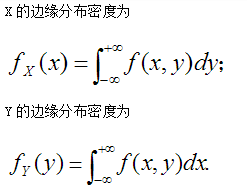
　（2）COV（X,Y）=E{[X-E（X)][Y-E（Y）]}=E(XY)-E(X)E(Y)-E(Y)E(X)+E(X)E(Y)
=E（XY）-EXEY
E(XY)等于在全平面上对xyf(x,y)关于x,y求二重积分，注意f(x,y)在不同区域具体形式不一样。
（2）ρ=$\frac{Cov(X,Y)}{\sqrt{D（X）}\sqrt{D（Y）}}$
D（X）=$E（X^2）+E（X{）}^2$

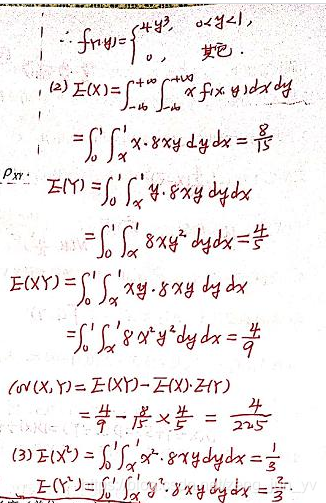
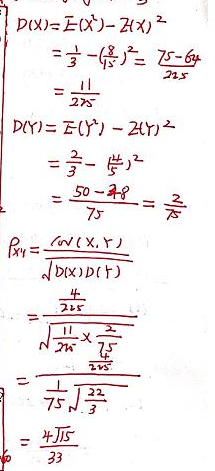
14.已知某种螺钉的直径 ~ ( $\mu$, ${\sigma }^2$) ，现抽取 9 枚测得其长度（单位：mm）如下：

14.7，15.0， 14.8，14.9，15.1，15.2，14.8，14.7，15.0

（1）求未知参数$\mu$, ${\sigma }^2$ 的极大似然估计；

(2)求参数 $\mu$ 的 95%的置信区间。

分析：
$S^2=\frac{1}{n-1}{\sum }_{i=1}^n(X_i-\overline{X}{)}^2$

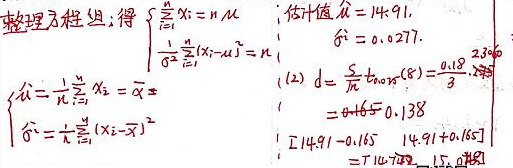
拓展：

15．某种矿砂的 5 个样品中的含镍量（%）经测定为：

3.24 3.20 3.24 3.26 3.22

设含镍量服从正态分布，问在$\alpha$ =0.01 下能否接收假设：这批矿砂的含镍量小于 3.25?

分析：

$S^2=\frac{1}{n-1}{\sum }_{i=1}^n(X_i-\overline{X}{)}^2$

拓展:参数估计