栈

作用	函数	方法作用
定义栈	Stack$⟨char⟩s$	定义一个char型的栈
元素访问：	s.top()	返回栈顶
容量：	s.empty()	返回是否为空
	s.size()	返回堆的大小
修改：	s.push()	插入传入的参数到栈顶
	s.pop()	弹出栈顶

括号匹配+Java栈

队列

作用	函数	方法作用
定义栈	queue$⟨int⟩q$	定义一个int型的队列
元素访问：	[优先队列]q.top()/q.front()	访问队首
容量：	q.empty()	返回是否为空
	q.size()	返回堆的大小
修改：	q.push()	插入元素在队尾
	q.pop()	删除队首元素
	q.clear()	清空队列

优先队列和堆一样有两种形式：最大优先队列和最小优先队列。
1.如果直接定义一个优先队列，系统默认的为降序优先队列。

 priority_queue<int>q;

2. 可以通过系统默认的已有的结构greater$⟨T⟩$来定义一个升序的优先队列。与greate$⟨T⟩$类似的是less$⟨T⟩$。

#include <iostream>
#include<queue>
#include<ctime>
#include<cstdlib>
#include<vector>
using namespace std;int main()
{srand(time(NULL));priority_queue<int,vector<int>,greater<int> >q;//注意空格for(int i=10;i>0;i--)q.push(rand());while(!q.empty()){cout<<q.top()<<endl;q.pop();}return 0;
}

3.如果队列元素为某结构体，可以通过重载<符号来进行自定义优先级，这里必须要注意的是只能是<并且在重载函数还需要加上const！

#include <iostream>
#include<queue>
#include<ctime>
#include<cstdlib>
#include<vector>
using namespace std;struct node
{int data;bool operator<(const node&a)const{return data>a.data;    //此时是升序，如果是<则是降序}
};int main()
{srand(time(NULL));priority_queue<node>q;for(int i=10;i>0;i--){node t;t.data=rand();q.push(t);}while(!q.empty()){cout<<q.top().data<<endl;q.pop();}return 0;
}

4.结构体定义优先级还有种方式，可以不加const，但需要定义为友元。

struct node
{int data;friend bool operator <(const node a,const node b)  //!!!{return a.data>b.data;    //此时是升序，如果是<则是降序}
};

5.对于结构体的定义，当在使用优先级定义时，根据其是堆的特性，还可以有如下定义优先级的方式。

#include <iostream>
#include<queue>
#include<ctime>
#include<cstdlib>
#include<vector>
using namespace std;struct node
{int data;
};
struct nodeCmp
{bool operator()(const node &a,const node &b)//注意写法{return a.data>b.data; //此时为升序，<为降序}
};int main()
{srand(time(NULL));priority_queue<node,vector<node>,nodeCmp>q;  //此处定义与之前方式不同for(int i=10;i>0;i--){node t;t.data=rand();q.push(t);}while(!q.empty()){cout<<q.top().data<<endl;q.pop();}return 0;
}

链表

天梯赛模拟 链表去重 (25 分)

单向链表

单向链表中包含数据域和指针域，其中数据域用于存放数据，指针域用来连接当前结点和下一节点。

struct Node {int value;Node *next;
};

双向链表

双向链表中同样有数据域和指针域，不同之处在于指针域有左右（或上一个、下一个）之分，用来连接上一个节点、当前结点、下一个结点。

struct Node {int value;Node *left;Node *right;
};

向链表中插入（写入）数据

单向链表

void insertNode(int i, Node *p) {Node *node = new Node;node->value = i;node->next = p->next;p->next = node;
}

单向循环链表

上面介绍了简单的单向链表的插入数据，有时我们会将链表的头尾连接起来将链表变为循环链表

void insertNode(int i, Node *p) {Node *node = new Node;node->value = i;node->next = NULL;if (p == NULL) {p = node;node->next = node;} else {node->next = p->next;p->next = node;}
}

由于是循环的链表，我们在插入数据时需要判断原链表是否为空，为空则自身循环，不为空则正常插入数据循环。具体过程可参考下面这张图。

双向循环链表

void insertNode(int i, Node *p) {Node *node = new Node;node->value = i;if (p == NULL) {p = node;node->left = node;node->right = node;} else {node->left = p;node->right = p->right;p->right->left = node;p->right = node;}
}

从链表中删除数据

单向（循环）链表

void deleteNode(Node *p) {p->value = p->next->value;Node *t = p->next;p->next = p->next->next;delete t;
}

从链表中删除某个结点时，将 p 的下一个结点 (p->next) 的值覆盖给 p 即可，与此同时更新 p 的下下个结点。具体过程可参考下面这张图。

双向循环链表

void deleteNode(Node *&p) {p->left->right = p->right;p->right->left = p->left;Node *t = p;p = p->right;delete t;
}

哈希表

哈希表是又称散列表，一种以 “key-value” 形式存储数据的数据结构。所谓以 “key-value” 形式存储数据，是指任意的 key 都唯一对应到内存中的某个位置。只需要输入查找的值 key，就可以快速地找到其对应的 value。可以把哈希表理解为一种高级的数组，这种数组的下标可以是很大的整数，浮点数，字符串甚至结构体。

哈希函数

要让 key 对应到内存中的位置，就要为 key 计算索引，也就是计算这个数据应该放到哪里。这个根据 key 计算索引的函数就叫做哈希函数，也称散列函数。举个例子，比如 key 是一个人的身份证号码，哈希函数就可以是号码的后四位，当然也可以是号码的前四位。生活中常用的“手机尾号”也是一种哈希函数。在实际的应用中，key 可能是更复杂的东西，比如浮点数、字符串、结构体等，这时候就要根据具体情况设计合适的哈希函数。哈希函数应当易于计算，并且尽量使计算出来的索引均匀分布。

在 OI 中，最常见的情况应该是 key 为整数的情况。当 key 的范围比较小的时候，可以直接把 key 作为数组的下标，但当 key 的范围比较大，比如以 $10^9$范围内的整数作为 key 的时候，就需要用到哈希表。一般把 key 模一个较大的质数作为索引，也就是取 $f(x)=x$ $mod$ $M$ 作为哈希函数。另一种比较常见的情况是 key 为字符串的情况，在 OI 中，一般不直接把字符串作为 key，而是先算出字符串的哈希值，再把其哈希值作为 key 插入到哈希表里。

能为 key 计算索引之后，我们就可以知道每个 value 应该放在哪里了。假设我们用数组 a 存放数据，哈希函数是 f，那键值对 (key,value) 就应该放在 a[f(key)]上。不论 key 是什么类型，范围有多大，f(key) 都是在可接受范围内的整数，可以作为数组的下标。

冲突

如果对于任意的 key，哈希函数计算出来的索引都不相同，那只用根据索引把 (key,value) 放到对应的位置就行了。但实际上，常常会出现两个不同的 key，他们用哈希函数计算出来的索引是相同的。这时候就需要一些方法来处理冲突。在 OI 中，最常用的方法是拉链法。

拉链法

拉链法也称开散列法（open hashing）。
拉链法是在每个存放数据的地方开一个链表，如果有多个 key 索引到同一个地方，只用把他们都放到那个位置的链表里就行了。查询的时候需要把对应位置的链表整个扫一遍，对其中的每个数据比较其 key 与查询的 key 是否一致。如果索引的范围是 1~M，哈希表的大小为 N，那么一次插入/查询需要进行期望 $O(\frac{N}{M})$次比较。

const int maxn = 1000000;
const int M = 999997;
struct HashTable
{struct Node{int next, value, key;} data[maxn];int head[M], maxn;int f(int key){return key % M;}int get(int key){for (int p = head[f(key)]; p; p = data[p].next)if (data[p].key == key)return data[p].value;return -1;}int modify(int key, int value){for (int p = head[f(key)]; p; p = data[p].next)if (data[p].key == key)return data[p].value = value;}int add(int key, int value){if (get(key) != -1)return -1;data[++maxn] = (Node){head[f(key)], value, key};head[f(key)] = maxn;return value;}
};

这边再为大家提供一个封装过的模板，可以像 map 一样用，并且较短

struct hash_map    // 哈希表模板
{struct data{long long u;int v, nex;};                // 前向星结构data e[SZ << 1];  // SZ 是 const int 表示大小int h[SZ], cnt;int hash(long long u){return u % SZ;}int& operator[](long long u){int hu = hash(u);  // 获取头指针for (int i = h[hu]; i; i = e[i].nex)if (e[i].u == u)return e[i].v;return e[++cnt] = (data) {u, -1, h[hu]}, h[hu] = cnt, e[cnt].v;}hash_map(){cnt = 0;memset(h, 0, sizeof(h));}
};

解释一下，hash 函数是针对 key 的类型设计的，并且返回一个链表头指针用于查询。在这个模板中我们写了一个(long long ,int) 式的 hash 表，并且当某个 key 不存在的时侯初始化对应的 val 成 -1。hash_map() 函数是在定义的时侯初始化用的。

闭散列法

闭散列方法把所有记录直接存储在散列表中，如果发生冲突则根据某种方式继续进行探查。
比如线性探查法：如果在 d 处发生冲突，就依次检查 d + 1，d+2……

const int N = 360007;  // N 是最大可以存储的元素数量
class Hash
{
private:int keys[N];int values[N];public:Hash(){memset(values, 0, sizeof(values));}int& operator[](int n){// 返回一个指向对应 Hash[Key] 的引用// 修改成不为 0 的值 0 时候视为空int idx = (n % N + N) % N, cnt = 1;while (keys[idx] != n && values[idx] != 0){idx = (idx + cnt * cnt) % N;cnt += 1;}keys[idx] = n;return values[idx];}
};

并查集

并查集是一种树形的数据结构，顾名思义，它用于处理一些不交集的 合并 及 查询 问题。 它支持两种操作：

• 查找（Find）：确定某个元素处于哪个子集(优化在路径压缩)；
• 合并（Union）：将两个子集合并成一个集合。
  （1）Friendly Group Gym - 102769F 2020（并查集）ccpc秦皇岛分站赛
  （2）UVA10129 Play on Words （并查集判连通+欧拉回路）
  （3）Ice_cream’s world I HDU - 2120（并查集判环）

启发式合并（按秩合并）

一个祖先突然抖了个机灵：「你们家族人比较少，搬家到我们家族里比较方便，我们要是搬过去的话太费事了。」

由于需要我们支持的只有集合的合并、查询操作，当我们需要将两个集合合二为一时，无论将哪一个集合连接到另一个集合的下面，都能得到正确的结果。但不同的连接方法存在时间复杂度的差异。具体来说，如果我们将一棵点数与深度都较小的集合树连接到一棵更大的集合树下，显然相比于另一种连接方案，接下来执行查找操作的用时更小（也会带来更优的最坏时间复杂度）。

当然，我们不总能遇到恰好如上所述的集合点数与深度都更小。鉴于点数与深度这两个特征都很容易维护，我们常常从中择一，作为估价函数。而无论选择哪一个，时间复杂度都为$O(max(m,n))$ 。

在算法竞赛的实际代码中，即便不使用启发式合并，代码也往往能够在规定时间内完成任务。
如果只使用启发式合并，而不使用路径压缩，时间复杂度为$O(m$ $log$ $n)$ 。由于路径压缩单次合并可能造成大量修改，有时路径压缩并不适合使用。例如，在可持久化并查集、线段树分治 + 并查集中，一般使用只启发式合并的并查集。

此处给出一种 C++ 的参考实现，其选择点数作为估价函数：

std::vector<int> size(N, 1);  // 记录并初始化子树的大小为 1
void unionSet(int x, int y) {int xx = find(x), yy = find(y);if (xx == yy) return;if (size[xx] > size[yy])  // 保证小的合到大的里swap(xx, yy);fa[xx] = yy;size[yy] += size[xx];
}

带权并查集

（1）How Many Answers Are Wrong HDU - 3038（带权并查集）
（2）Rochambeau POJ - 2912 （枚举和加权并查集+路径压缩）找唯一裁判
我们还可以在并查集的边上定义某种权值、以及这种权值在路径压缩时产生的运算，从而解决更多的问题。比如对于经典的「NOI2001」食物链，我们可以在边权上维护模 3 意义下的加法群。

其他应用

种类并查集：
Find them, Catch them POJ - 1703（种类并查集）
最小生成树算法 中的 Kruskal 和 最近公共祖先 中的 Tarjan 算法是基于并查集的算法。

堆

堆是一棵树，其每个节点都有一个键值，且每个节点的键值都大于等于/小于等于其父亲的键值。
每个节点的键值都大于等于其父亲键值的堆叫做小根堆，否则叫做大根堆。STL 中的 priority_queue 其实就是一个大根堆。
（小根）堆主要支持的操作有：插入一个数、查询最小值、删除最小值、合并两个堆、减小一个元素的值。
习惯上，不加限定提到“堆”时往往都指二叉堆。

二叉堆

从二叉堆的结构说起，它是一棵二叉树，并且是完全二叉树，每个结点中存有一个元素（或者说，有个权值）。
堆性质：父亲的权值不小于儿子的权值（大根堆）。同样的，我们可以定义小根堆。本文以大根堆为例。
由堆性质，树根存的是最大值（getmax 操作就解决了）。

插入操作

插入操作是指向二叉堆中插入一个元素，要保证插入后也是一棵完全二叉树。
最简单的方法就是，最下一层最右边的叶子之后插入。
如果最下一层已满，就新增一层。

• 插入之后可能会不满足堆性质？
  向上调整：如果这个结点的权值大于它父亲的权值，就交换，重复此过程直到不满足或者到根。插入之后向上调整后，没有其他结点会不满足堆性质。

向上调整的时间复杂度是$O(log$ $n)$ 的。

删除操作

删除操作指删除堆中最大的元素，即删除根结点。
但是如果直接删除，则变成了两个堆，难以处理。
所以不妨考虑插入操作的逆过程，设法将根结点移到最后一个结点，然后直接删掉。
然而实际上不好做，我们通常采用的方法是，把根结点和最后一个结点直接交换。
于是直接删掉（在最后一个结点处的）根结点，但是新的根结点可能不满足堆性质……
向下调整：在该结点的儿子中，找一个最大的，与该结点交换，重复此过程直到底层。删除并向下调整后，没有其他结点不满足堆性质。
时间复杂度 $O(log$ $n)$ 。

减小某个点的权值

很显然，直接修改后，向上调整一次即可，时间复杂度为 。

实现

我们发现，上面介绍的几种操作主要依赖于两个核心：向上调整和向下调整。
考虑使用一个序列 h 来表示堆$h_i$。 的两个儿子分别是$h_{2i}$ 和 $h_{2i+1}$， 1是根结点：

参考代码：

void up(int x) {while (x > 1 && h[x] > h[x / 2]) {swap(h[x], h[x / 2]);x /= 2;}
}
void down(int x) {while (x * 2 <= n) {t = x * 2;if (t + 1 <= n && h[t + 1] > h[t]) t++;if (h[t] <= h[x]) break;std::swap(h[x], h[t]);x = t;}
}

建堆

考虑这么一个问题，从一个空的堆开始，插入n 个元素，不在乎顺序。
直接一个一个插入需要 $O(log$ $n)$ 的时间，有没有更好的方法？

方法一：使用 decreasekey（即，向上调整）

从根开始，按 BFS 序进行。

void build_heap_1() {for (i = 1; i <= n; i++) up(i);
}

方法二：使用向下调整

这时换一种思路，从叶子开始，逐个向下调整

void build_heap_2() {for (i = n; i >= 1; i--) down(i);
}

对顶堆

维护一个序列，支持两种操作：
1.向序列中插入一个元素
2.输出并删除当前序列的中位数（若序列长度为偶数，则输出较小的中位数）

这个问题可以被进一步抽象成：动态维护一个序列上第 k大的数，k 值可能会发生变化。
对于此类问题，我们可以使用 对顶堆 这一技巧予以解决（可以避免写权值线段树或 BST 带来的繁琐）。
对顶堆由一个大根堆与一个小根堆组成，小根堆维护大值即前 k大的值（包含第 k 个），大根堆维护小值即比第k 大数小的其他数。
这两个堆构成的数据结构支持以下操作：

• 维护：当小根堆的大小小于k 时，不断将大根堆堆顶元素取出并插入小根堆，直到小根堆的大小等于k ；当小根堆的大小大于 k时，不断将小根堆堆顶元素取出并插入大根堆，直到小根堆的大小等于 k；
• 插入元素：若插入的元素大于等于小根堆堆顶元素，则将其插入小根堆，否则将其插入大根堆，然后维护对顶堆；
• 查询第 k 大元素：小根堆堆顶元素即为所求；
• 删除第 k 大元素：删除小根堆堆顶元素，然后维护对顶堆；
• k 值+1/-1 ：根据新的 k值直接维护对顶堆。

显然，查询第 k 大元素的时间复杂度是$(1)$ 的。由于插入、删除或调整 值后，小根堆的大小与期望的 k 值最多相差 1，故每次维护最多只需对大根堆与小根堆中的元素进行一次调整，因此，这些操作的时间复杂度都是 $O(log$ $n)$ 的。

#include <cstdio>
#include <iostream>
#include <queue>
using namespace std;
int t, x;
int main() {scanf("%d", &t);while (t--) {// 大根堆，维护前一半元素（存小值）priority_queue<int, vector<int>, less<int> > a;// 小根堆，维护后一半元素（存大值）priority_queue<int, vector<int>, greater<int> > b;while (scanf("%d", &x) && x) {// 若为查询并删除操作，输出并删除大根堆堆顶元素// 因为这题要求输出中位数中较小者（偶数个数字会存在两个中位数候选）// 这个和上面的第k大讲解有稍许出入，但如果理解了上面的，这个稍微变通下便可理清if (x == -1) {printf("%d\n", a.top());a.pop();}// 若为插入操作，根据大根堆堆顶的元素值，选择合适的堆进行插入else {if (a.empty() || x <= a.top())a.push(x);elseb.push(x);}// 对堆顶堆进行调整if (a.size() > (a.size() + b.size() + 1) / 2) {b.push(a.top());a.pop();} else if (a.size() < (a.size() + b.size() + 1) / 2) {a.push(b.top());b.pop();}}}return 0;
}

左偏树

左偏树是一种 可并堆，具有堆的性质，并且可以快速合并。

dist 的定义和性质

对于一棵二叉树，我们定义 外节点 为左儿子或右儿子为空的节点，定义一个外节点的 dist 为 1，一个不是外节点的节点dist 为其到子树中最近的外节点的距离加一。空节点的 dist为0 。

注：很多其它教程中定义的 dist都是本文中的 dist 减去1 ，本文这样定义是因为代码写起来方便。

一棵有n 个节点的二叉树，根的 dist不超过 $[log(n+1)]$，因为一棵根的 dist为x 的二叉树至少有x-1层是满二叉树，那么就至少有$2^x-1$ 个节点。注意这个性质是所有二叉树都具有的，并不是左偏树所特有的。

左偏树的定义和性质

左偏树是一棵二叉树，它不仅具有堆的性质，并且是「左偏」的：每个节点左儿子的 都大于等于右儿子的dist 。
因此，左偏树每个节点的dist 都等于其右儿子的 dist加一。
需要注意的是， dist不是深度，左偏树的深度没有保证，一条向左的链也是左偏树。

核心操作：合并（merge)

合并两个堆时，由于要满足堆性质，先取值较小（为了方便，本文讨论小根堆）的那个根作为合并后堆的根节点，然后将这个根的左儿子作为合并后堆的左儿子，递归地合并其右儿子与另一个堆，作为合并后的堆的右儿子。为了满足左偏性质，合并后若左儿子的 dist小于右儿子的dist ，就交换两个儿子。
参考代码：

int merge(int x, int y) {if (!x || !y) return x | y;  // 若一个堆为空则返回另一个堆if (t[x].val > t[y].val) swap(x, y);  // 取值较小的作为根t[x].rs = merge(t[x].rs, y);          // 递归合并右儿子与另一个堆if (t[t[x].rs].d > t[t[x].ls].d)swap(t[x].ls, t[x].rs);   // 若不满足左偏性质则交换左右儿子t[x].d = t[t[x].rs].d + 1;  // 更新distreturn x;
}

由于左偏性质，每递归一层，其中一个堆根节点的 dist 就会减小1 ，而“一棵有n 个节点的二叉树，根的 dist 不超过$[log(n+1)]$ ”，所以合并两个大小分别为n 和 m 的堆复杂度是$O(log$ $n+log$ $m)$ 。

左偏树还有一种无需交换左右儿子的写法：将 较大的儿子视作左儿子， 较小的儿子视作右儿子：

int& rs(int x) { return t[x].ch[t[t[x].ch[1]].d < t[t[x].ch[0]].d]; }
int merge(int x, int y) {if (!x || !y) return x | y;if (t[x].val < t[y].val) swap(x, y);rs(x) = merge(rs(x), y);t[x].d = t[rs(x)].d + 1;return x;
}

左偏树的其它操作

• 插入节点
  单个节点也可以视为一个堆，合并即可。
• 删除根
  合并根的左右儿子即可。
• 删除任意节点
  做法
  先将左右儿子合并，然后自底向上更新 dist、不满足左偏性质时交换左右儿子，当 dist无需更新时结束递归：

int& rs(int x) { return t[x].ch[t[t[x].ch[1]].d < t[t[x].ch[0]].d]; }// 有了 pushup，直接 merge 左右儿子就实现了删除节点并保持左偏性质
int merge(int x, int y) {if (!x || !y) return x | y;if (t[x].val < t[y].val) swap(x, y);t[rs(x) = merge(rs(x), y)].fa = x;pushup(x);return x;
}void pushup(int x) {if (!x) return;if (t[x].d != t[rs(x)].d + 1) {t[x].d = t[rs(x)].d + 1;pushup(t[x].fa);}
}

整个堆加上/减去一个值、乘上一个正数

其实可以打标记且不改变相对大小的操作都可以。

在根打上标记，删除根/合并堆（访问儿子）时下传标记即可：

int merge(int x, int y) {if (!x || !y) return x | y;if (t[x].val > t[y].val) swap(x, y);pushdown(x);t[x].rs = merge(t[x].rs, y);if (t[t[x].rs].d > t[t[x].ls].d) swap(t[x].ls, t[x].rs);t[x].d = t[t[x].rs].d + 1;return x;
}
int pop(int x) {pushdown(x);return merge(t[x].ls, t[x].rs);
}

随机合并

int merge(int x, int y) {if (!x || !y) return x | y;if (t[y].val < t[x].val) swap(x, y);if (rand() & 1)  //随机选择是否交换左右子节点swap(t[x].ls, t[x].rs);t[x].ls = merge(t[x].ls, t[y]);return x;
}

可以看到该实现方法唯一不同之处便是采用了随机数来实现合并，这样一来便可以省去 dist的相关计算。且平均时间复杂度亦为$O(log$ $n)$ ，

块状数据结构

分块思想

块状数组

块状链表

树分块

Sqrt Tree

单调栈

单调栈中存放的数据应该是有序的，所以单调栈也分为单调递增栈和单调递减栈

• 单调递增栈：单调递增栈就是从栈底到栈顶数据是从大到小
• 单调递减栈：单调递减栈就是从栈底到栈顶数据是从小到大

stack<int> st;
//此处一般需要给数组最后添加结束标志符，具体下面例题会有详细讲解
for (遍历这个数组)
{if (栈空 || 栈顶元素大于等于当前比较元素){入栈;}else{while (栈不为空 && 栈顶元素小于当前元素){栈顶元素出栈;更新结果;}当前数据入栈;}
}

单调队列

//在“尾部”添加元素x
while (l != r && mq[r] <= x) r--;
mq[++r] = x;//查询队首元素
if (l != r) printf("%d\n", mq[l+1]);
else printf("-1\n");//弹出队首元素
if (l != r) l++;

树状数组

(1)蓝桥杯2014届试题9题 小朋友排队（树状数组+类逆序对）
(2)A Simple Problem with Integers POJ - 3468（线段树+区间查询+区间修改+建树+懒惰标记模板）+（树状数组）
(3)Minimum Inversion Number HDU - 1394(求一个数字环的逆序对+多种解法)
树状数组的代码要比线段树短得多，思维也更清晰，在解决一些单点修改的问题时，树状数组是不二之选。
如果要具体了解树状数组的工作原理，请看下面这张图：

这个结构的思想和线段树有些类似：用一个大节点表示一些小节点的信息，进行查询的时候只需要查询一些大节点而不是更多的小节点。
最下面的八个方块就代表存入a中的八个数，现在都是十进制。
他们上面的参差不齐的剩下的方块就代表 的上级——c 数组。
很显然看出：
$c_2$管理的是 $a_1$&$a_2$；
$c_4$管理的是 $a_1$&$a_2$&$a_3$&$a_4$；
$c_6$管理的是 $a_5$&$a_6$；
$c_8$则管理全部 8个数。
所以，如果你要算区间和的话，比如说要算 ~ 的区间和，暴力算当然可以，那上百万的数，那就 TLE 喽。

那么这种类似于跳一跳的连续跳到中心点而分值不断变大的原理是一样的（倍增）。

你从 开始往前跳，发现 （ 我也不确定是多少，算起来太麻烦，就意思一下）只管 这个点，那么你就会找 ，发现 管的是 &；那么你就会直接跳到 ， 就会管 ~ 这些数，下次查询从 往前找，以此类推。

用法及操作

那么问题来了，你是怎么知道 管的 的个数分别是多少呢？你那个 1 个， 2个， 8个……是怎么来的呢？ 这时，我们引入一个函数——lowbit：

int lowbit(int x) {// 算出x二进制的从右往左出现第一个1以及这个1之后的那些0组成数的二进制对应的十进制的数return x & -x;
}

lowbit 的意思注释说明了，咱们就用这个说法来证明一下a[88] ：
$88_{(10)}=1011000_{(2)}$
发现第一个1 以及他后面的 0组成的二进制是 $1000_{(2)}=8_{(10)}$
1000对应的十进制是8 ，所以 c 一共管理 8个a 。
这就是 lowbit 的用处，仅此而已（但也相当有用）。

您可能又问了：x & -x 是什么意思啊？

在一般情况下，对于 int 型的正数，最高位是 0，接下来是其二进制表示；而对于负数 (-x)，表示方法是把 x 按位取反之后再加上 1。

例如 :

那么对于 单点修改 就更轻松了：

void add(int x, int k) {while (x <= n) {  // 不能越界c[x] = c[x] + k;x = x + lowbit(x);}
}

每次只要在他的上级那里更新就行，自己就可以不用管了。

int getsum(int x) {  // a[1]……a[x]的和int ans = 0;while (x >= 1) {ans = ans + c[x];x = x - lowbit(x);}return ans;
}

区间加 & 区间求和

若维护序列a的差分数组 b，此时我们对a 的一个前缀r 求和，即${\sum }_{i=1}^r{a}_i$ ，由差分数组定义得 $a_i=$${\sum }_{j=1}^i{b}_j$
进行推导

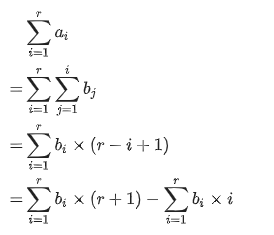
区间和可以用两个前缀和相减得到，因此只需要用两个树状数组分别维护$\sum b_i$ 和$\sum i\ast b_i$ ，就能实现区间求和。

代码如下

int t1[MAXN], t2[MAXN], n;inline int lowbit(int x) { return x & (-x); }void add(int k, int v) {int v1 = k * v;while (k <= n) {t1[k] += v, t2[k] += v1;k += lowbit(k);}
}int getsum(int *t, int k) {int ret = 0;while (k) {ret += t[k];k -= lowbit(k);}return ret;
}void add1(int l, int r, int v) {add(l, v), add(r + 1, -v);  // 将区间加差分为两个前缀加
}long long getsum1(int l, int r) {return (r + 1ll) * getsum(t1, r) - 1ll * l * getsum(t1, l - 1) -(getsum(t2, r) - getsum(t2, l - 1));
}

Tricks $O(n)$建树：

每一个节点的值是由所有与自己直接相连的儿子的值求和得到的。因此可以倒着考虑贡献，即每次确定完儿子的值后，用自己的值更新自己的直接父亲。

// O(n)建树
void init() {for (int i = 1; i <= n; ++i) {t[i] += a[i];int j = i + lowbit(i);if (j <= n) t[j] += t[i];}
}

$O(log$ $n)$查询第k 小/大元素。在此处只讨论第k 小，第 k 大问题可以通过简单计算转化为第k 小问题。
将所有数字看成一个可重集合，即定义数组 a表示值为 i 的元素在整个序列重出现了 $a_i$次。找第 k 大就是找到最小的x 恰好满足 ${\sum }_{i=1}^x,a_i>=k$
因此可以想到算法：如果已经找到 x 满足 ${\sum }_{i=1}^x,a_i>=k$，考虑能不能让 x 继续增加，使其仍然满足这个条件。找到最大的x 后，x+1 就是所要的值。 在树状数组中，节点是根据 2 的幂划分的，每次可以扩大 2 的幂的长度。令sum 表示当前的 x所代表的前缀和，有如下算法找到最大的 x：

1. 求出$depth=\lfloor lo{g}_{2}n\rfloor$
2. 计算$t={\sum }_{i=x+1}^{x+2^{depth}}{a}_i$
3. 如果sum+t<=k ，则此时扩展成功，将$2^{depth}$ 累加到 x 上；否则扩展失败，对 x 不进行操作
   将 depth减 1，回到步骤 2，直至 depth 为 0

//权值树状数组查询第k小
int kth(int k) {int cnt = 0, ret = 0;for (int i = log2(n); ~i; --i) {      // i与上文depth含义相同ret += 1 << i;                      // 尝试扩展if (ret >= n || cnt + t[ret] >= k)  // 如果扩展失败ret -= 1 << i;elsecnt += t[ret];  // 扩展成功后 要更新之前求和的值}return ret + 1;
}

时间戳优化：

对付多组数据很常见的技巧。如果每次输入新数据时，都暴力清空树状数组，就可能会造成超时。因此使用tag 标记，存储当前节点上次使用时间（即最近一次是被第几组数据使用）。每次操作时判断这个位置tag 中的时间和当前时间是否相同，就可以判断这个位置应该是 0 还是数组内的值。

//时间戳优化
int tag[MAXN], t[MAXN], Tag;
void reset() { ++Tag; }
void add(int k, int v) {while (k <= n) {if (tag[k] != Tag) t[k] = 0;t[k] += v, tag[k] = Tag;k += lowbit(k);}
}
int getsum(int k) {int ret = 0;while (k) {if (tag[k] == Tag) ret += t[k];k -= lowbit(k);}return ret;
}

线段树

(1)Mayor’s posters POJ - 2528 （离散化+线段树）
(2)Balanced Lineup POJ - 3264（线段树模板+查询比大小+建树）
(3)Just a Hook HDU - 1698（查询区间求和+最基础模板）
(4)Assign the task HDU - 3974（线段树+dfs建树+单点查询+区间修改）
李超线段树
区间最值操作 & 区间历史最值
划分树
二叉搜索树 & 平衡树
跳表
可持久化数据结构
树套树
K-D Tree
珂朵莉树
动态树
析合树

/**▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒
▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒░░░░░░░░░░▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒
▒▒▒▒▒▒▒▒▒▒▒▒▒░░░░░░░░░░░░░░░░░░░▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒
▒▒▒▒▒▒▒▒▒▒░░░░░░░░░░░░░░░░░░░░░░░░░▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒
▒▒▒▒▒▒▒▒░░░░░░░░░░░░░░░░░░░░░░░░░░░░░▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒
▒▒▒▒▒▒░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░▄░░▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒
▒▒▒▒▒░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░██▌░░▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒
▒▒▒▒░░░░░░░░░░░░░░░░░░░░░░░░░░░▄▄███▀░░░░▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒
▒▒▒░░░░░░░░░░░░░░░░░░░░░░░░░░░█████░▄█░░░░▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒
▒▒░░░░░░░░░░░░░░░░░░░░░░░░░░▄████████▀░░░░▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒
▒▒░░░░░░░░░░░░░░░░░░░░░░░░▄█████████░░░░░░░▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒
▒░░░░░░░░░░░░░░░░░░░░░░░░░░▄███████▌░░░░░░░▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒
▒░░░░░░░░░░░░░░░░░░░░░░░░▄█████████░░░░░░░░▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒
▒░░░░░░░░░░░░░░░░░░░░░▄███████████▌░░░░░░░░▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒
▒░░░░░░░░░░░░░░░▄▄▄▄██████████████▌░░░░░░░░▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒
▒░░░░░░░░░░░▄▄███████████████████▌░░░░░░░░░▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒
▒░░░░░░░░░▄██████████████████████▌░░░░░░░░░▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒
▒░░░░░░░░████████████████████████░░░░░░░░░░▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒
▒█░░░░░▐██████████▌░▀▀███████████░░░░░░░░░░▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒
▐██░░░▄██████████▌░░░░░░░░░▀██▐█▌░░░░░░░░░▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒
▒██████░█████████ ░░░░░░░░░░▐█▐█▌░░░░░░░░░▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒
▒▒▀▀▀▀░░░██████▀░░░░░░░░░░░░▐█▐█▌░░░░░░░░▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒
▒▒▒▒▒░░░░▐█████▌░░░░░░░░░░░░▐█▐█▌░░░░░░░▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒
▒▒▒▒▒▒░░░░███▀██░░░░░░░░░░░░░█░█▌░░░░░░▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒
▒▒▒▒▒▒▒▒░▐██░░░██░░░░░░░░▄▄████████▄▄▄▄▄▄▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒
▒▒▒▒▒▒▒▒▒██▌░░░░█▄░░░░░░▄███████████████████▄▄▄▄▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒▒
▒▒▒▒▒▒▒▒▒▐██▒▒░░░██▄▄████████████████████████████████████████████
▒▒▒▒▒▒▒▒▒▒▐██▒▒▄█████████████████████████████████████████████████
▒▒▒▒▒▒▒▒▒▒▄▄█████████████████████████████████████████████████████
█████████████████████████████████████████████████████████████████*/