一:题目

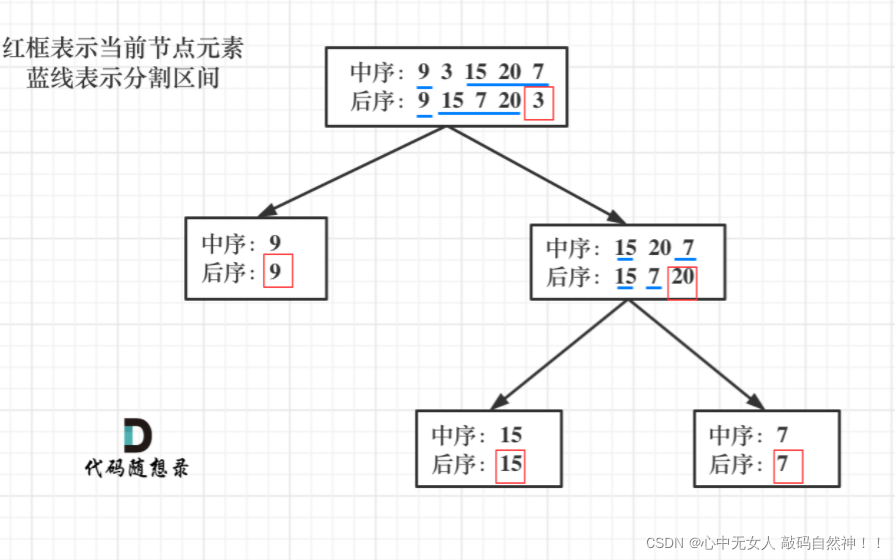
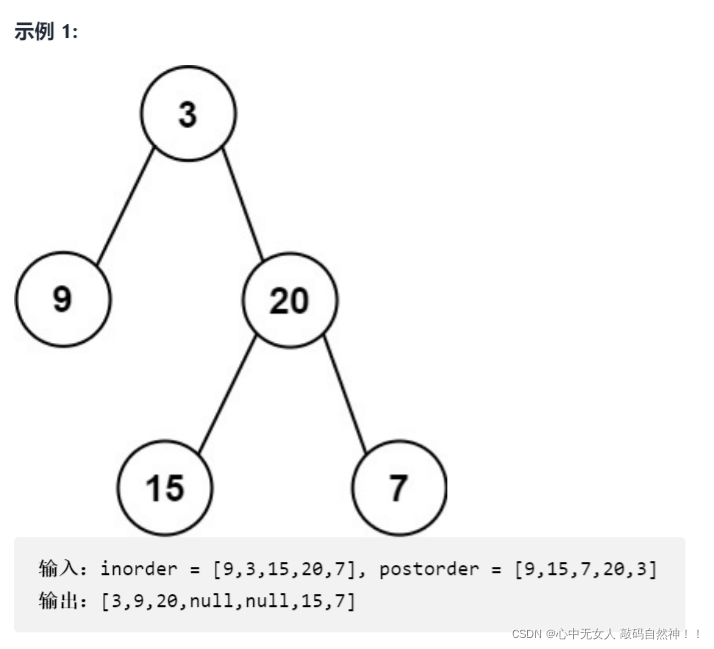
在这里插入图片描述

二:思路

在这里插入图片描述
例子:中序[9,3,15,20,7];后序[9,15,7,20,3]
1.我们先选取后续的最后的结点3（其是根节点）
2.我们在中序序列中用上一步求出的根节点3并记录其在中序数组中的位置rootin,然后我们就可以
求出左子树的结点个数（rootin - leftin）,同时右子树我们也可以找到范围
3.根据我们求出的左子树的结点个数,我们可以确定后序遍历序列中的（我们左右子树的范围）
4.接下来我们通过递归继续根据新的数组范围在后序序列中求出根节点，然后再在中序序列
中重新划分（左右子树）
//递归建造二叉树的左子树（所以我们需要中序中左子树的范围，后序中左子树的范围）
root->left = makeTree(中序左子树范围,后序左子树范围,中序序列,后序序列)
root->right = makeTree(中序右子树范围,后序右子树范围,中序序列,后序序列)

三:上码

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:/**思路:例子:中序[9,3,15,20,7];后序[9,15,7,20,3]1.我们先选取后续的最后的结点3（其是根节点）2.我们在中序序列中用上一步求出的根节点3并记录其在中序数组中的位置rootin,然后我们就可以求出 左子树的结点个数（rootin - leftin）,同时右子树我们也可以找到范围3.根据我们求出的左子树的结点个数,我们可以确定后序遍历序列中的（我们左右子树的范围）4.接下来我们通过递归 继续根据新的数组范围 在后序序列中求出根节点，然后再在中序序列中重新划分（左右子树）//递归建造二叉树的左子树（所以我们需要中序中左子树的范围，后序中左子树的范围）root->left = makeTree(中序左子树范围,后序左子树范围,中序序列,后序序列)  root->right = makeTree(中序右子树范围,后序右子树范围,中序序列,后序序列)  */TreeNode* makeTree(int leftin,int rightin,int leftpost,int rightpost,vector<int>&in,vector<int>&post) {if(leftin > rightin) return NULL;TreeNode* root = new TreeNode(post[rightpost]);int rootin = leftin;//求出中序序列中  根节点的下标while(rootin <= rightin && in[rootin] != post[rightpost]) rootin++;int leftTreeNums = rootin-leftin;//求出左子树中结点的个数 //rootin-1（rootin表示的是根节点的下标了 所以我们要刨去根节点）//leftpost+leftTreeNums-1同理 root->left = makeTree(leftin,rootin-1,leftpost,leftpost+leftTreeNums-1,in,post);root->right = makeTree(rootin+1,rightin,leftpost+leftTreeNums,rightpost-1,in,post);return root;}TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {TreeNode* root = makeTree(0,inorder.size()-1,0,postorder.size()-1,inorder,postorder);return root;}
};