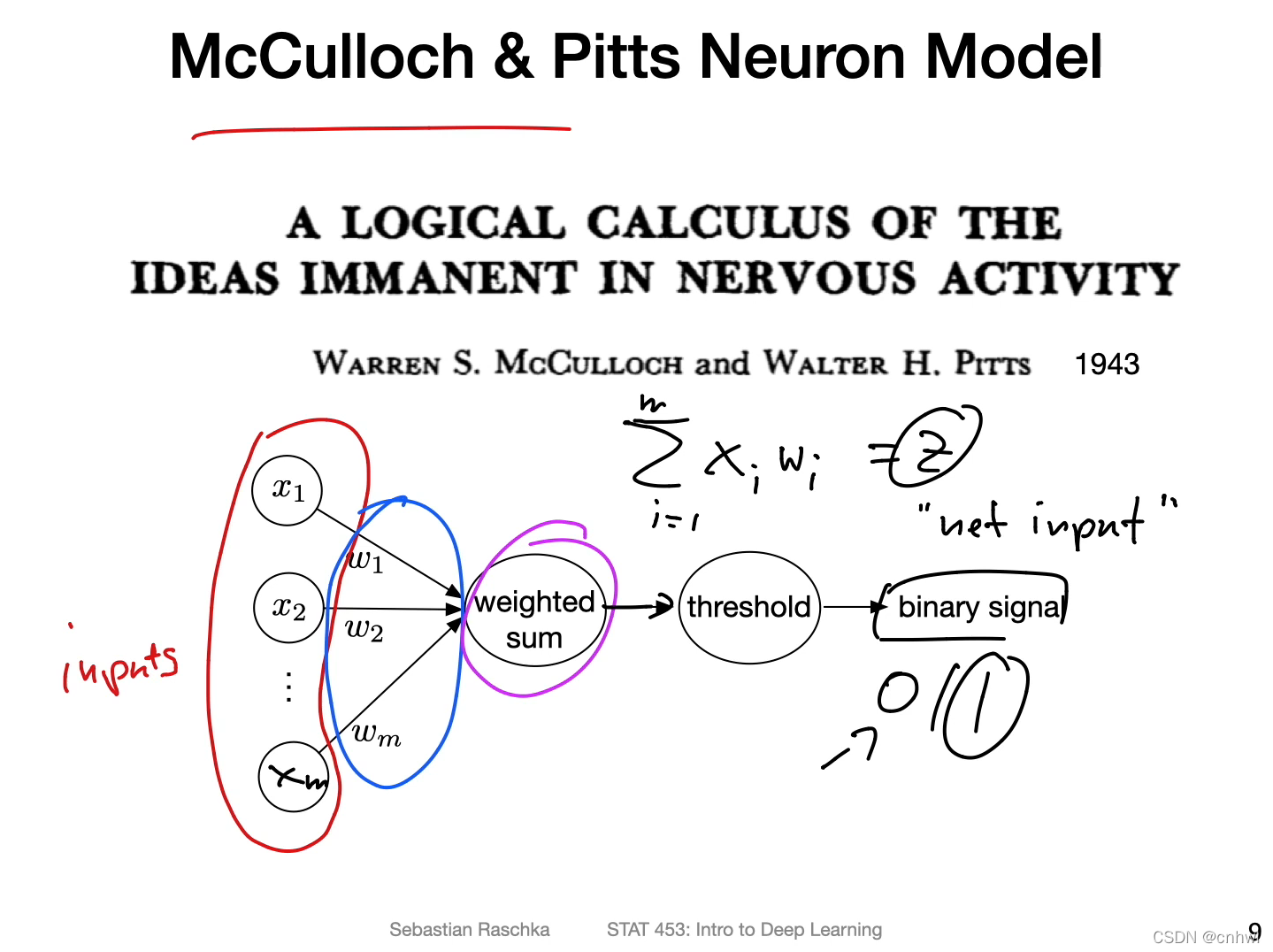
最经典的神经元模型，从左到右依次是：输入、权重、加权和、阈值、输出。加权和又叫做 Net Input，符号为 z，当 z 的值大于阈值时输出 1，小于阈值时输出 0。

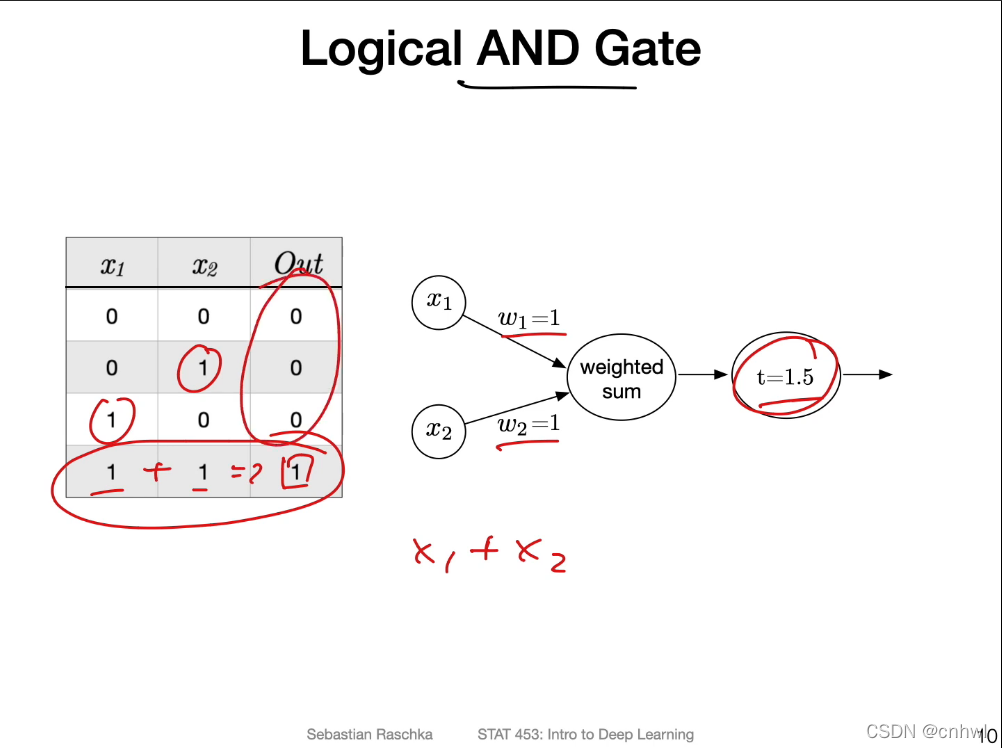
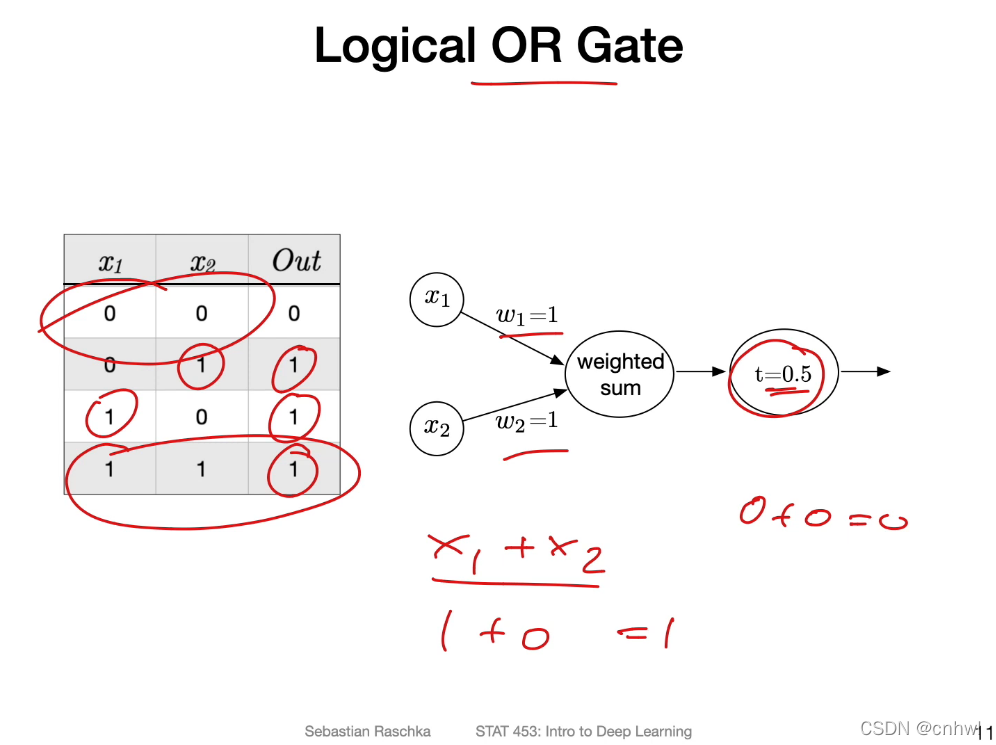
实现与门和或门，权重为 1，阈值分别为 1.5 和 0.5 即可。


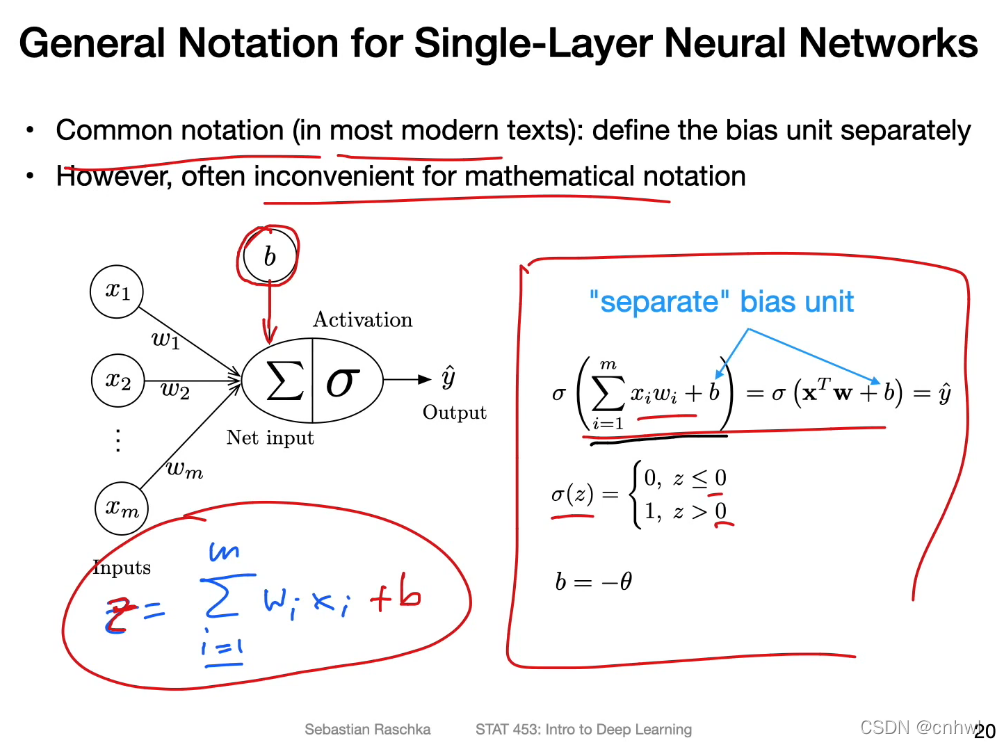
用偏置 b 代替负阈值，此时的加权和 z 就变成了 $w^{T}x+b$，新的阈值就是 0 了。

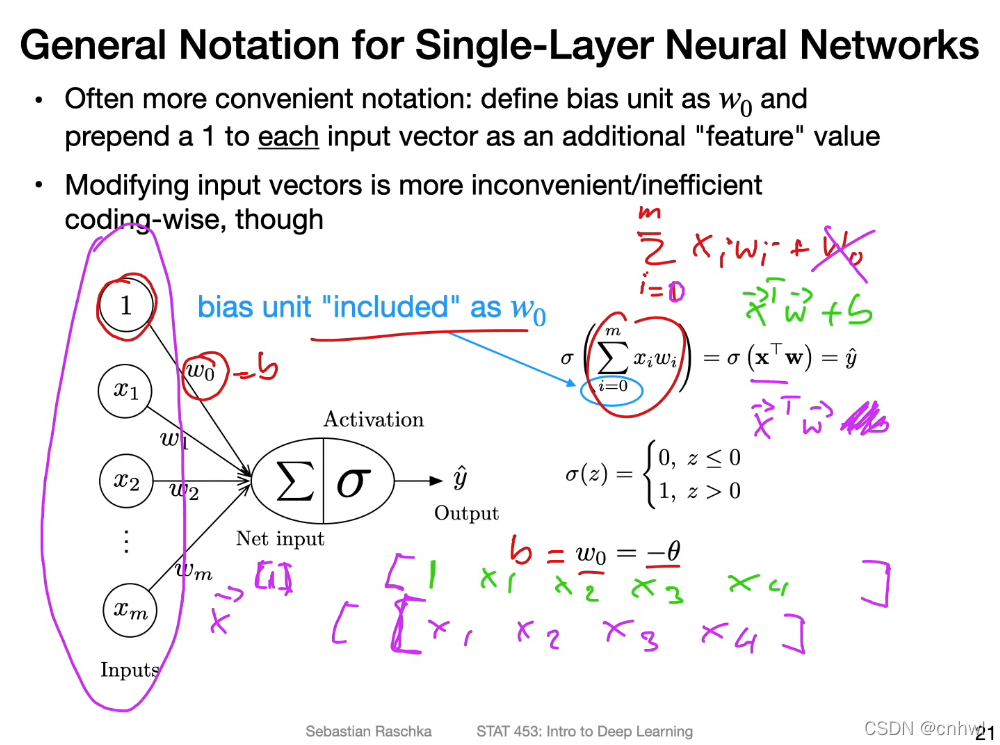
更进一步的，可以将偏置看作是输入 1 时对应的权重，这样做的好处是可以写成向量内积的形式，有利于数学表达。但是，实际常用的还是 $w^{T}x+b$，因为前面那种形式需要改变输入向量，操作上就是创建一个新的副本，比较麻烦。后者的话通过广播机制就能实现加 b 的操作，比较简单。

计算两个向量的内积，Python 的 for 循环是最慢的，其次是列表推导式，最快的是 Numpy 的点积 dot 函数，因为 Numpy 支持并行计算。

感知器的更新公式就两句话：如果预测为 -1 或 0（负例），实际为 1 （正例），就对权重 w 加上输入 x；如果预测为 1（正例），实际为 -1 或 0（负例），就对权重 w 减去输入 x

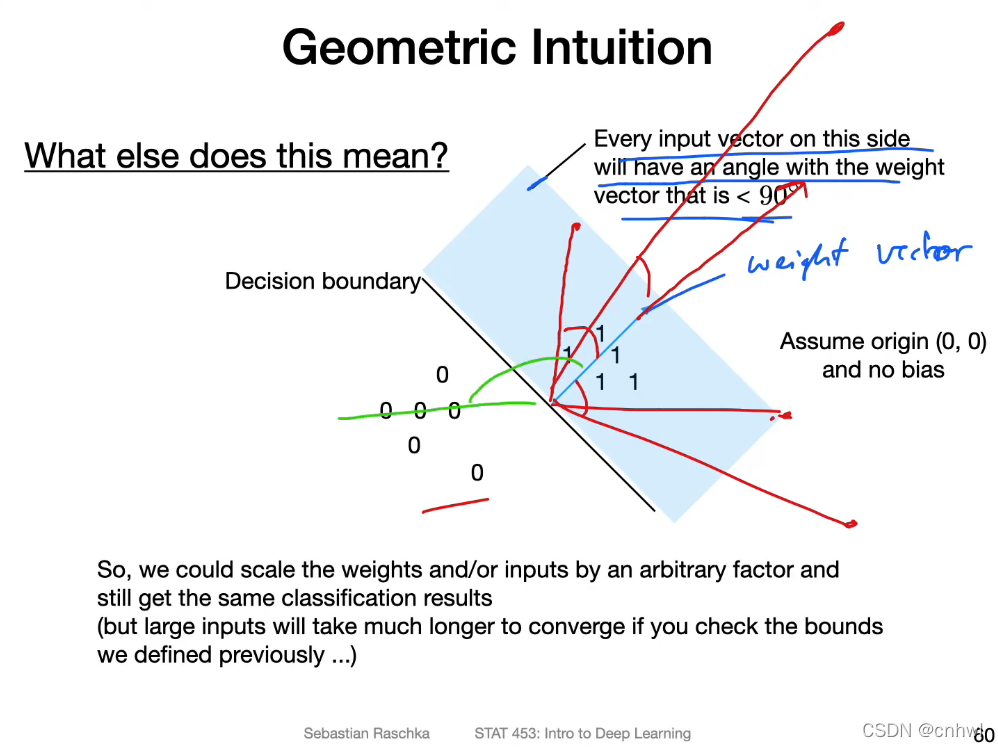
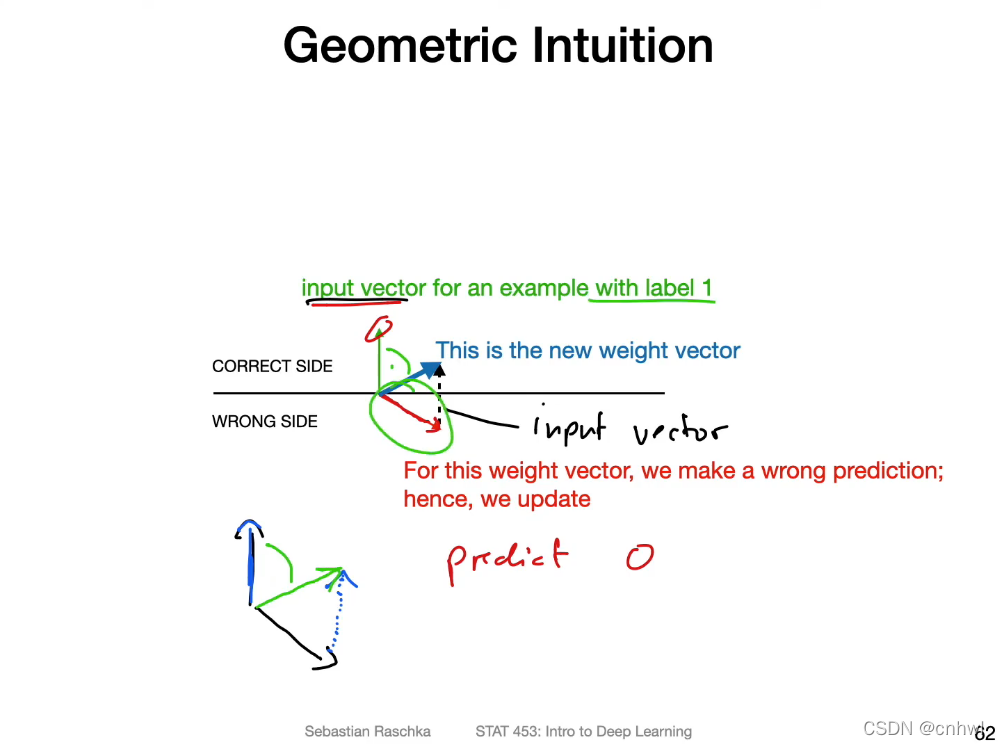
几何上直观理解，就是因为对于输入向量 x 来说，对它正确分类的超平面的权重向量（法向量） w，x 与 w 的夹角一定小于 90°，所以如果分错了，权重向量 w 与 x 的夹角大于 90 °，此时就可以通过加上输入向量 x，让新的权重向量 w 指向正确的方向。