分治算法,顾名思义就是“分而治之”,即把规模较大的复杂问题拆分为若干规模较小的类似子问题,并逐个解决,最后再将各个子问题的解决结果合并,得到原始问题的结果的方法。这个技巧是很多高效算法的基础,例如快速排序算法、归并排序算法、快速傅里叶变换等等。

五大常用算法之分治算法
分治算法的通俗理解
一般来说,规模小的问题比规模大的问题解决起来简单,例如数组排序问题,只有 2 个元素的数组处理起来要比有 2000 个元素的数组简单。这是分治算法的基本立足点,也是使用条件之一,总结一下就是,对于一个规模较大的问题,可以拆分成若干不相关的子问题,并且子问题解决起来更加简单。
分治算法在我们日常生活中无处不在,例如国家依次划分为省市县镇村来管理,本质上也是因为解决“子问题”(管理村)要简单许多。
有这样一个非常经典的问题:生产线生产了 99 个工件,其中 1 个工件是劣品,比其他 98 个工件质量轻一些,如果用天平称,至少多少次一定能找到这个劣品工件?
要解决这个问题,最简单粗暴的方法是逐个比较,如果第 x 个工件比第 y 个工件轻,第 x 个工件就是劣品。那么 99 个工件至少需要比较 50 次才能确保一定找到劣品。
逐个比较
能够发现,使用逐个比较的方法的时间开销与工件总数有关,如果工件总数很少,比如只有 2 个,那么只需要比较一次就可以找到劣品了。因此该问题满足使用“分治算法”的必要条件之一:规模较小的子问题解决起来更简单。现在尝试使用分治算法解决该问题:
- 将 99 个工件等分为 3 份,每份 33 个工件;
- 比较第 1、2 份,如果天平平衡,那么劣品必定在第 3 份中,否则劣品在轻的那一份中;
- 将劣品所在的那一份再等分为 3 份,每份 11 个工件;
- 重复第 2 步;
- 将劣品所在那一份再分为 3 份,每份分别为 3、3、2 个工件;
- 重复第 2 步;
- 不管劣品所在那一份为 3 个工件还是 2 个工件,只需再比较一次,就可找到劣品。
可见,使用分治算法只需要比较 4 次就可以找到劣品,这远低于逐个比较法的 50 次。不过也应该注意到,使用分治法找劣品时,每次拆分子问题时,各个子问题是互不干扰的——例如其中一份的 33 个工件质量不会影响其他份的 33 个工件质量。
归并排序法
从前面这个简单的实例可以看出,分治法有时的确能够极大的提升解决问题的效率,事实上,在C语言程序开发中,许多优秀的算法本质上都是基于分治思想的,一个非常典型的例子就是归并排序法,它在处理数组排序时有着不错的效率。
在处理数组排序时,如果数组中只有 1 个元素,那么该数组本身就可看作是排好序的数组。如果数组中有 2 个元素,那么最多只需比较一次就可以得到排好序的数组。这其实是归并排序法的核心,也即规模越小的数组,对其排序越简单。下图是一个长度为 5 的数组,为了排序,先把它拆分到不能继续拆为止。
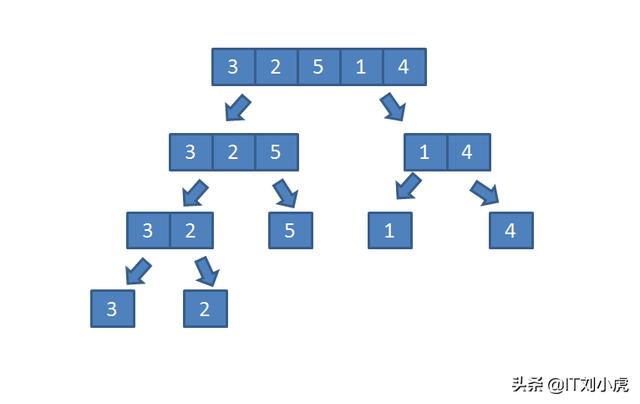
拆分到不能继续拆
显然,“拆分到不能继续拆”后,子问题已经变成了只有 1 个元素的数组,这样的数组已经是“排好序”的数组了。按照我们前面讨论的,现在需要做的就是把这些已经排好序的子数组合并,问题转化为:按照顺序合并有序数组,如下图所示:
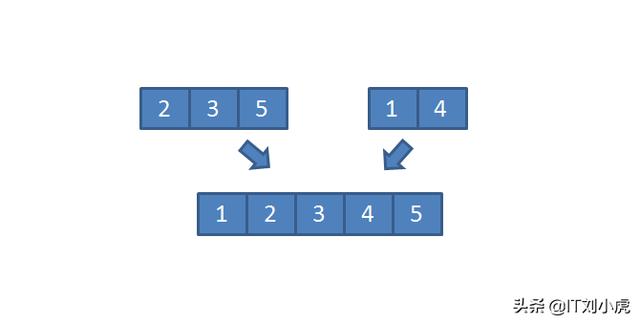
按照顺序合并有序数组
归并排序的C语言实现
根据前面的分析,使用C语言实现归并排序法需要实现两个子模块:拆分和合并。拆分数组有多种方法,通常采用二等分法,设数组头的索引为 start,数组尾的索引为 end,mid=(start+end)/2,每次平均拆分,都会将数组分为 start 到 mid,和 mid+1 到 end 两个子数组,再对这两个子数组执行同样的拆分,一直到不能拆分为止。所谓“不能拆分”,其实就是数组中只有一个元素,也即 start 等于 end,这一过程非常适合使用递归实现。我们先确定递归的停止条件:
void divide(int *arr, int start, int end){ if (start >= end) return;}否则,我们将继续拆分子数组(start, mid)和(mid+1, end),这一过程的C语言代码如下:
void divide(int *arr, int start, int end){ if (start >= end) return; int mid = (start+end)/2; divide(arr, start, mid); divide(arr, mid+1, end);}关于 divide() 递归函数的理解,我之前的这篇文章详细讨论过。
搞定拆分模块后,再来看看合并模块。按照前面讨论的,拆分到“不能拆为止”的都可认为是已经排好序的子数组,所以合并模块要按照顺序(本例从小到大)将子数组合并:
int merge(int *arr, int start, int mid, int end){ int ln = mid-start +1; int rn = end - mid; int left[ln], right[rn]; for (int i=0; i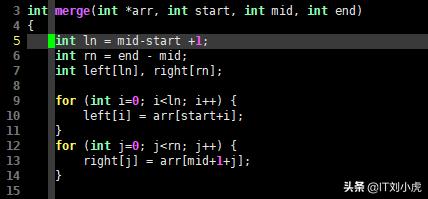
C语言代码1
我们先将要合并的拆分后的两个子数组分别保存在 left 和 right 数组里,应注意,这里使用了C语言的变长数组语法,因此在编译时要指定-std=c99选项。接着,我们逐个比较 left 和 right 中的元素,按照顺序填入 arr,这一过程的C语言代码如下所示:
int merge(int *arr, int start, int mid, int end){... int i=0, j=0, k=0; for (k = start; i < ln && j < rn; ++k) { if (left[i] < right[j]) { arr[k] = left[i]; ++i; } else { arr[k] = right[j]; ++j; } }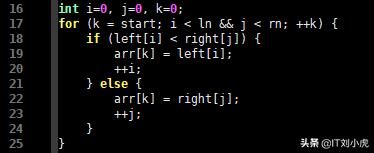
C语言代码2
执行完毕后,left 和 right 中可能还有剩余元素,这些剩余元素必定是需要放在 arr 后部分的,因此C语言代码可以如下写:
int merge(int *arr, int start, int mid, int end){... if (i < ln) for (; i < ln; i++) { arr[k] = left[i]; ++k; } if (j < rn) for (; j < rn; ++j) { arr[k] = right[j]; ++k; }}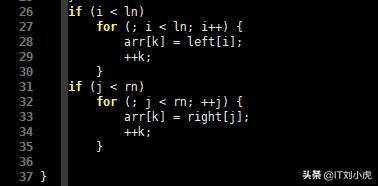
C语言代码3
到这里,merge() 函数就完成了,将之与 divide() 函数组合起来,也即:
void divide(int *arr, int start, int end){ if (start >= end) return; int mid = (start+end)/2; divide(arr, start, mid); divide(arr, mid+1, end); merge(arr, start, mid, end);}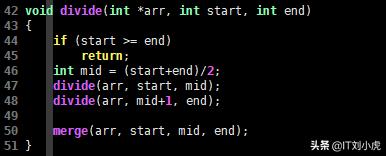
C语言代码4
现在 divide() 函数便可对输入的数组 arr 排序了。
测试归并排序法
这里使用 8 个元素的数组做测试:
int main(){ int arr[8] = {1, 3, 2, 5, 8, 7, 6, 4}; divide(arr, 0, 7); for (int i=0; i<8; i++) printf("%d ", arr[i]); printf(""); return 0;}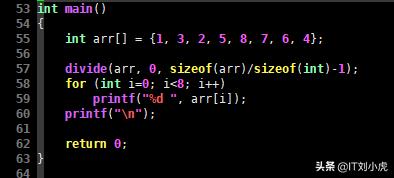
C语言代码5
编译并执行这段C语言代码,得到如下输出:
# gcc t.c -std=c99# ./a.out 1 2 3 4 5 6 7 8归并排序算法的时间复杂度
在计算过程中,累加和比较的过程是关键操作,一个长度为 n 的数组在递归的每一层都会进行 n 次操作,分治法的递归层级在 logN 级别,所以整体的时间复杂度是 O(nlogn)。
归并排序法是一个效率不错的排序算法,可能时间复杂度看起来不是特别直观,我们将之与简单粗暴的“冒泡排序算法”对比,在我的机器上分别对不同规模的数组排序,得到如下结果:
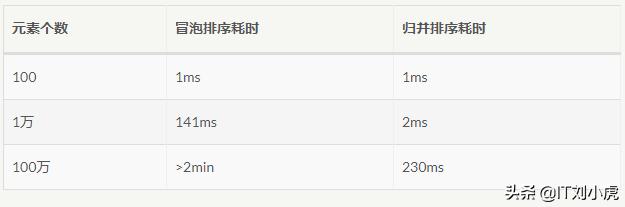
排序效率对比
冒泡排序算法是比较简单的算法,在处理规模较小的数组时和归并排序法的效率不相上下,但是在处理规模较大的数组时,冒泡排序算法的效率逐渐远离归并排序了,且数组的规模越大,二者的效率差异越大,在处理 100 万个数组元素时,归并排序算法仅消耗 230 毫秒就处理完毕了,而冒泡排序算法在执行 2 分钟后仍然还没有完成,我没有耐心等下去,提前结束它了。








python选择题word打印版)

方法的使用教程)
)




-智能合约Solidity)
)

