使用 CNN 处理图像问题已经是常规操作,但此类方法会造成局部位置信息的损失。如何解决这个问题呢?来自中科院自动化所和北京中医药大学的研究者另辟蹊径,提出用图卷积网络解决语义分割问题。
选自arXiv,作者:Yi Lu等,机器之心编译,参与:魔王、杜伟。

论文链接:https://arxiv.org/pdf/2001.00335.pdf
使用深度学习执行语义分割在图像像素分类方面取得了巨大进步。但是,深度学习提取高级特征时往往忽略了局部位置信息(local location information),而这对于图像语义分割而言非常重要。
为了避免上述问题,来自中科院自动化所、北京中医药大学的研究者们提出一个执行图像语义分割任务的图模型 Graph-FCN,该模型由全卷积网络(FCN)进行初始化。
首先,通过卷积网络将图像网格数据扩展至图结构数据,这样就把语义分割问题转换成了图节点分类问题;然后,使用图卷积网络解决图节点分类问题。
研究者称,这是首次将图卷积网络用于图像语义分割的尝试。该方法在 VOC 数据集上获得了有竞争力的 mIOU 性能,相比原始 FCN 模型有 1.34% 的性能提升。
语义分割问题的难点
语义分割是计算机视觉领域中的重要课题,其复杂程度超过分类和检测任务。这项密集预测任务需要预测每个像素的类别,也就是说它需要从高级语义信息和局部位置信息中学习目标轮廓、目标位置和目标类别。
基于深度学习的语义分割方法,具体而言即卷积神经网络(CNN),为该领域带来了一系列巨大进展。提取高级特征的强大泛化能力使得图像分类和检测任务取得了非常好的性能,但伴随泛化而来的局部位置信息损失则为密集预测任务增加了难度。具备较大感受野的高级语义信息对应卷积神经网络中的小型特征图,这类图会造成像素级局部位置信息的损失。
多种基于深度学习的方法对该问题带来了改进,如全卷积网络 [16]、Segent [1]、Deeplab 方法 [2,3,4]。这些工作使用全连接层、空洞卷积和金字塔结构,来减少提取高级特征过程中的位置信息损失。
中科院等提出语义分割难题新解法
首先,研究者为图像语义分割问题构建图节点模型。图模型方法广泛应用于分割问题,这类方法将像素视作节点,将节点之间的差异度(dissimilarity)视作边(edge)。最优的分割即对图执行最大割(maximum cut)。
结合了概率论和图论的概率图模型方法(如马尔可夫随机场和条件随机场)被用于细化语义分割结果。这些方法将检测到的目标建模为图节点,通过提取目标之间的关系来改进检测准确率。相比于深度卷积模型把输入数据表示为网格结构,图模型具备更灵活的跳跃连接(skip connection),因此它可以探索图中节点之间的关系。
受限于计算量,研究者使用 FCN 初始化该图模型。该图模型基于小尺寸图像构建,其节点标注由 FCN 进行初始化,边的权重则由高斯核函数进行初始化。
然后使用图卷积网络(GCN)解决这个图模型。GCN 是处理图结构数据的当前最优模型之一。基于节点的 GCN 利用消息传播(message propagation)来交换相邻节点之间的信息。这一过程可以在图的较大相邻范围内提取特征,其作用类似于卷积网络中的卷积层和池化层。由于该过程中不会有节点消失,因此基于节点的 GCN 扩展了感受野,并避免了局部位置信息出现损失。
这篇论文提出了新型模型 Graph-FCN 来解决语义分割问题。研究者使用深度卷积网络建模图,并首次用 GCN 方法解决图像语义分割任务。Graph-FCN 可以扩大感受野,同时避免局部位置信息出现损失。实验表明,Graph-FCN 的性能优于 FCN。
Graph-FCN 方法详解
GCN 旨在解决图结构数据集上的学习问题。图结构数据可看作是三元组 G(N, E, U),其中 N 表示图的节点集合,即 |N| ∗ S 矩阵(|N| 表示图节点数量,S 表示节点标注向量的维度)。E 是图的边集合。U 对应图特征,由于本研究涉及任务与 U 无关,因此本研究不讨论 U。
与欧几里德空间中的数据表示不同,矩阵 N 和边 E 并非独特表示。矩阵 N 与 E 对应,它们都按照节点的顺序排列。研究者使用监督学习方式训练模型。节点 n_j 表示图 j 中的节点集,t_j 表示节点集 n_j 的标注集。因此用于语义分割任务的图模型可公式化为:
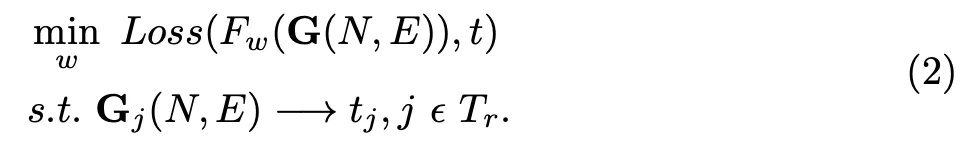
研究者将交叉熵函数作为该模型的损失函数。T_r 表示训练集。
节点
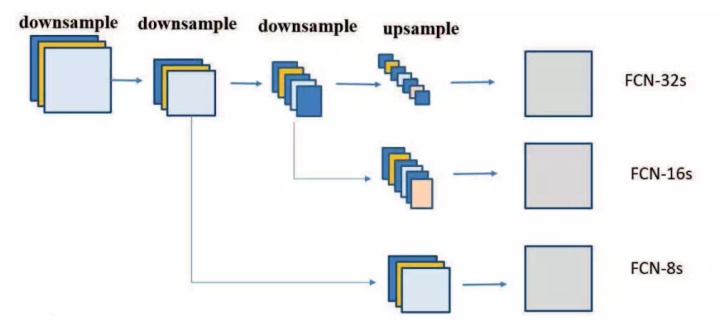
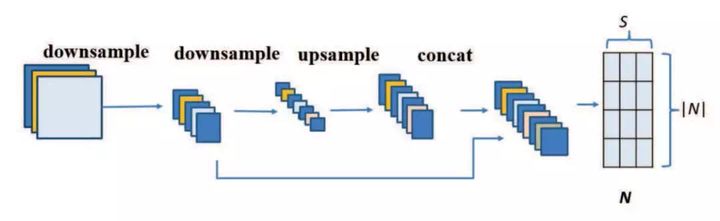
在本研究提出的新模型中,节点标注由 FCN-16s 进行初始化。通过端到端训练后,FCN-16s 得到步幅为 16 和 32 的特征图,如下图 2 所示。对步幅为 16 的特征图执行因子为 2 的上采样可以获得与步幅为 32 的特征图一样的大小。(节点 j 的)标注 x_j 由这两个特征向量以及特征图中每个节点位置的级联进行初始化。该标注包含在局部感受野上提取到的特征。在训练过程中,研究者通过对原始标注图像执行池化操作来得到节点标签。
边
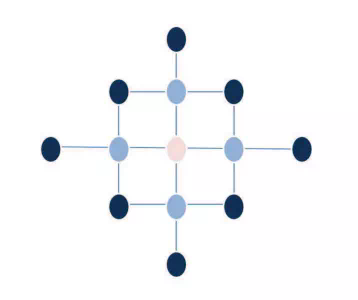
在图模型中,边和邻接矩阵相关。假设每个节点和其最邻近的 l 个节点相连,这意味着节点标注可以通过图神经网络中的边进行迁移。下图 3 中的示例描述了图神经网络中的感受野。假设 l 为 4,那么从相关距离的影响来看,我们需要用高斯核函数获得权重邻接矩阵 A。
使用 Graph-FCN 进行训练
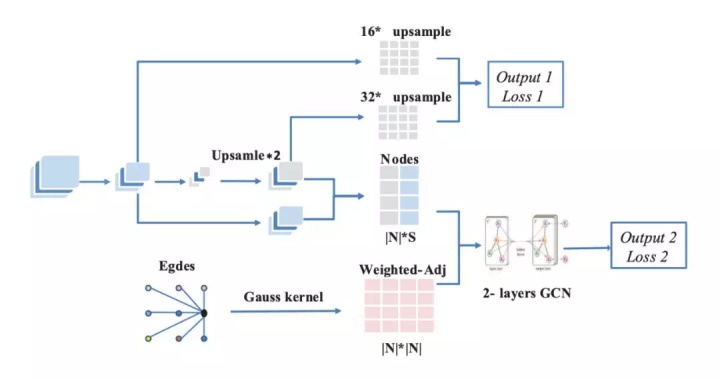
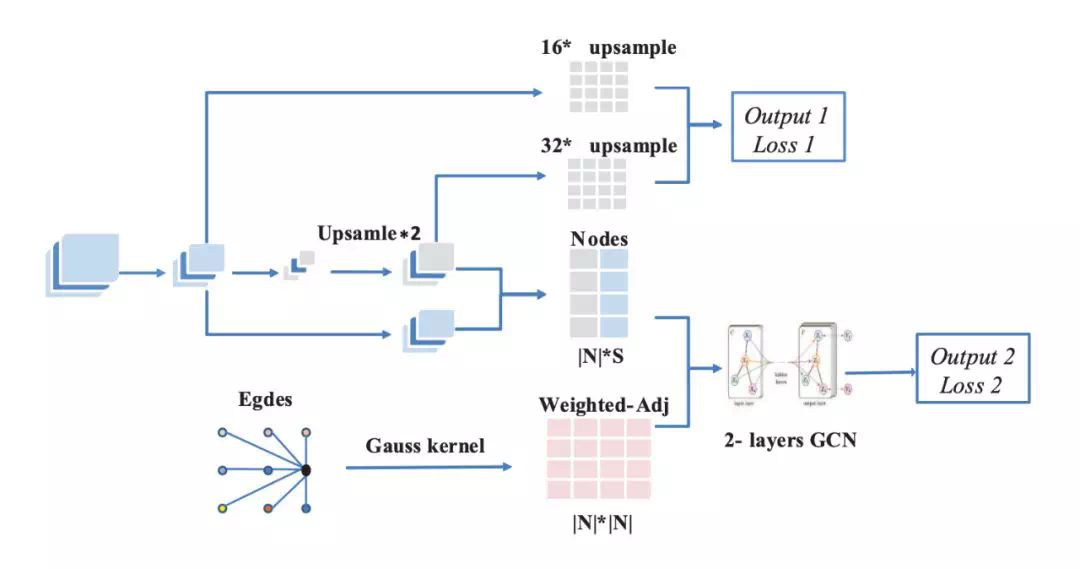
在 Graph-FCN 中,FCN-16s 实现节点分类和图模型在小型特征图中的初始化。同时,双层 GCN 获取图中节点的分类结果。研究者分别计算这两部分输出的交叉熵损失。和 FCN-16s 模型一样,Graph-FCN 也以端到端模式进行训练。Graph-FCN 网络结构如下图 4 所示:
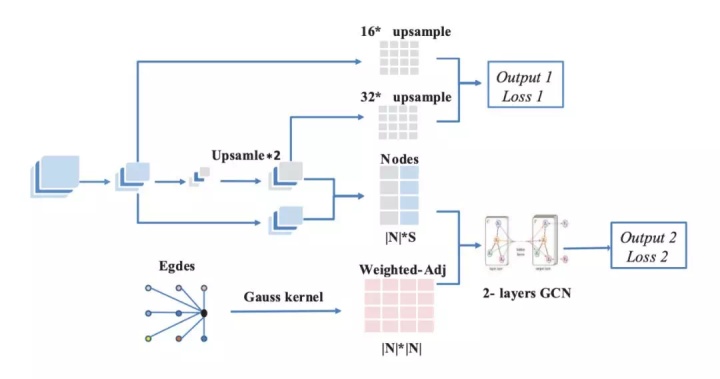
图 4:Graph-FCN 的结构示意图。该模型有两个输出和两个损失 L1 和 L2。它们共享卷积层提取特征的权重。L1 通过 output1 计算得到,L2 通过 output2 计算得到。通过最小化 L1 和 L2,FCN-16s 的性能得到了提升。
实验
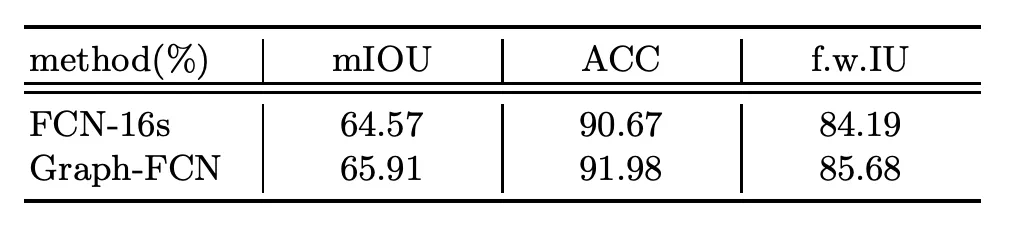
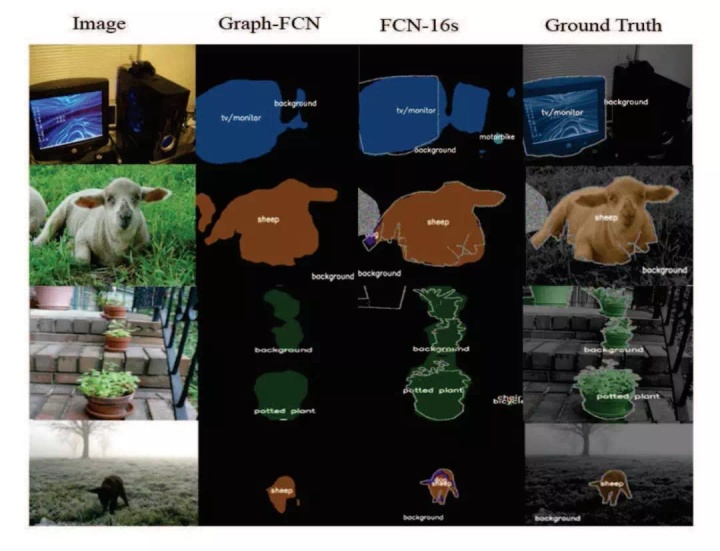
研究者在 VOC2012 数据集上对模型进行测试,实验结果表明 Graph-FCN 的性能优于原始 FCN 模型。

python选择题word打印版)

方法的使用教程)
)




-智能合约Solidity)
)








