6段Python代码刻画深度学习历史：从最小二乘法到深度神经网络

最小二乘法

深度学习的一切都起源于这个数学片段（我把它用Python 写了出来）：

这一方法是 1805 年巴黎数学家阿德利昂·玛利·埃·勒让德首次提出的（1805，Legendre），勒让德建立了许多重要的定理，尤其是在数论和椭圆积分（Elliptic Integrals）方面，提出了对素数定理（Prime Number Theorem）和二次互反律（Quadratic Reciprocity）的猜测并发表了初等几何教科书。他对预测彗星的未来位置特别痴迷。他找到了根据彗星此前的几个位置计算其轨迹的方法。

他尝试了几种方法，终于找到了一个让他满意的方法。勒让德先猜测彗星的未来位置，然后平方其误差，重新做出猜测，以减少平方误差的和。这是线性回归的种子。

上述代码中，m 是系数，b是预测中的常数，坐标是彗星的位置。我们的目标是找到m和b的组合，使其误差尽可能小。

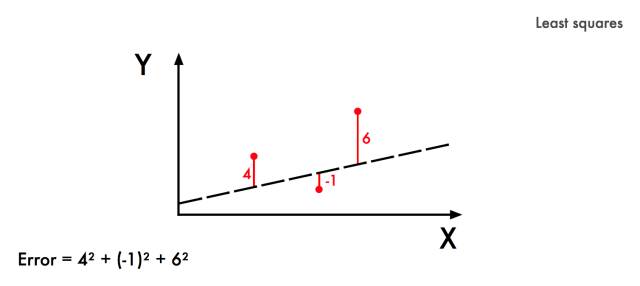
这就是深度学习的核心理念：输入，然后设定期望的输出，找到二者的相关性。

梯度下降

勒让德手工降低误差率的方法很耗时。荷兰诺贝尔奖得主Peter Debye 在一个世纪后（1909年，Debye）正式确定了解决方案。

让我们想象一下，勒让德有一个参数需要担心——我们称之为X。Y轴表示每个X的误差值。勒让德寻找的是最低误差时X的位置。在这种图形化表示中，我们可以看到误差Y最小化时，X = 1.1。

彼得·德比（Peter Debye）注意到最低点左边的斜率是负的，而另一边则是正的。因此，如果知道任何给定X值的斜率值，就可以将Y 导向最小值。

这引出了梯度下降的方法。几乎每一个深度学习模型中都在使用这个原则。

写成Python：

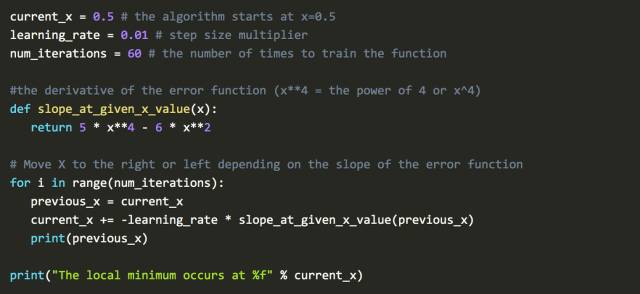
这里要注意的是learning_rate。通过沿斜率相反方向接近最小值。此外，越接近最小值，斜率越小。每一步都会减少，因为斜率向零趋近。

num_iterations 是达到最小值前的预计迭代次数。

线性回归

通过组合最小二乘法和梯度下降法，就可以得到线性回归。 20世纪50年代和60年代，一批实验经济学家在早期的计算机上实现了这个想法。这个逻辑是在卡片计算机上实现的，那是真正的手工软件程序。当时需要几天的时间准备这些打孔卡，最多24小时才能通过计算机进行一次回归分析。

现在用不着打孔卡了，用Python 写出来是这样的：

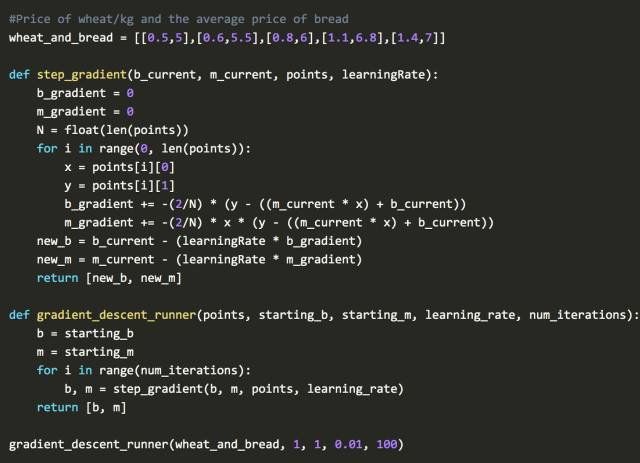
将误差函数与梯度下降合并可能会有一点不好理解。可以运行代码试一试。

感知器

查查弗兰克·罗森布拉特（Frank Rosenblatt）这个人——他白天解剖大鼠的大脑，并在夜间寻找外星生命的迹象。1958 年，他造了一个模仿神经元的机器（1958，Rosenblatt ），登上了“纽约时报”的头版《新海军装备学习》。

如果你给Rosenblatt的机器看50组图像，每组中的一张标有“向左”，另一张标着“向右”，这台机器能够在没有预编程的情况下对它们进行区分。公众被机器真正能学习的这种可能性吸引了。

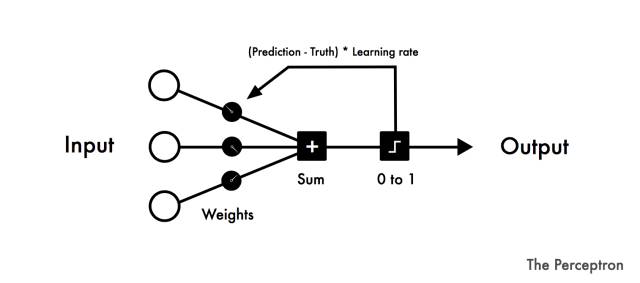
对于每个训练周期，您从左侧输入数据。初始随机权重添加到所有输入数据上。权重之和被计算出来。如果和为负，则被写为0，否则写为1。

如果预测是正确的，那么该循环中的权重就不做任何调整。如果有错误的，就将误差乘以学习率。这会相应地调整权重。

把感知器写成Python：

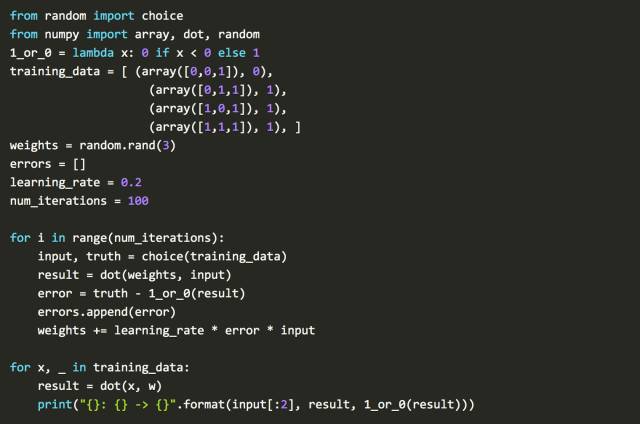
经过头一年的炒作，Marvin Minsky 和Seymour Papert 否定了这个想法(1969, Minsky& Papert)。当时，, Minsky 和 Papert 都在麻省理工学院的AI实验室工作。他们写了一本书，证明感知器只能解决线性问题。他们还驳斥了关于多层感知器的想法。不幸的是，弗兰克·罗森布拉特两年后遭遇了海难。

在, Minsky 和 Papert 专著出版一年之后，芬兰的一名大学生发现了解决多层感知器的非线性问题的理论（Linnainmaa，1970）。由于感知器遭受的批评，AI相关投资枯竭了十多年。这被称为AI 的第一个寒冬。

Minsky 和 Papert 的批评是XOR Problem。逻辑与OR逻辑相同，但有一个例外 - 当你有两个true语句（1＆1）时，返回False（0）。

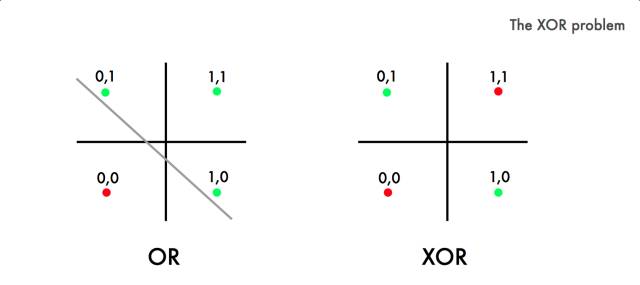
在 OR 逻辑中，可能将 true combination 从 false 中分离出来。但如你所见，你无法将 XOR 和一个线性函数分离。

人工神经网络

到1986年，几项实验证明了，神经网络可以解决复杂的非线性问题（Rumelhart等，1986）。当时的计算机比理论提出时快了一万倍。这时，Rumelhart提出了他们具有传奇色彩的论文：

我们描述了神经元式单元网络的新的学习过程，反向传播。该过程反复地调整网络中的连接权重，以便最小化网络的实际输出向量与期望的输出向量之间的差异。作为权重调整的结果，不属于输入或输出的内部“隐藏”单元代表了任务域的重要特征，并且任务中的规则由这些单元的交互捕获。创造有用的新函数的能力将反向传播与早期更简单的方法区分开来，例如感知器收敛过程“Nature 323,533-536（1986年10月9日）。

这一方法解决了XOR问题，解冻了第一个AI 寒冬。

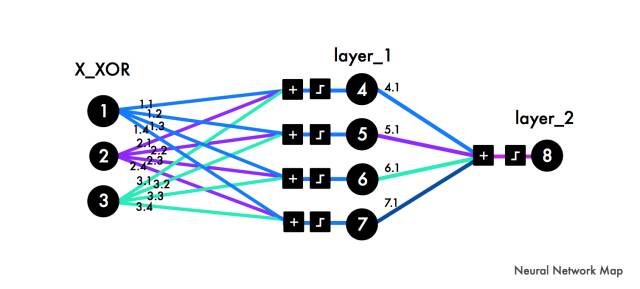
请注意，X_XOR数据中添加的参数[1]是偏置神经元，它们与线性函数中的常量具有相同的行为。

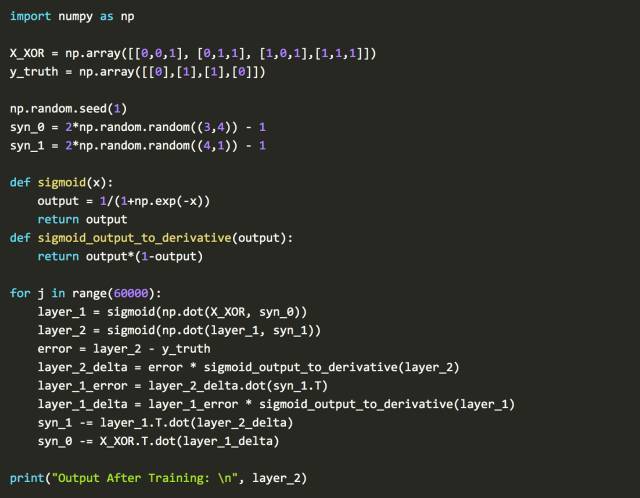
反向传播、矩阵乘法和梯度下降组合可能很难包围你的头脑。这个过程的可视化通常是对发生事情的简化。请专注于理解背后的逻辑。

深度神经网络

深层神经网络是输入层和输出层之间具有很多层的神经网络。这个概念是由Rina Dechter（Dechter，1986）引入的，但在2012年获得了主流关注。不久之后就出现了IBM Watson 的Jeopardy 大胜和谷歌识猫的成功。

深度神经网络的核心结构保持不变，但现在应用于几个不同的问题。正则化也有很多改进。最初，这是一组数学函数，来简化嘈杂的数据（Tikhonov，A.N，1963）。它们现在用于神经网络，以提高其泛化能力。

创新的很大一部分是原因计算能力的飞跃。它改进了研究者的创新周期——80年代中期的超级计算机需要计算一年的东西，今天GPU 技术半秒就能算好。

计算方面的成本降低以及深度学习库的发展现在已经众所周知。我们来看一个普通的深度学习的例子，从底层开始：

GPU > Nvidia Tesla K80。硬件常用于图形处理。与CPU相比，深度学习平均速度要快50-200倍。
CUDA > GPU的低级编程语言
CuDNN > Nvidia 优化 CUDA的库
Tensorflow > Google 在 CuDNN 之上的深度学习框架
TFlearn > Tensorflow的前端框架

我们来看看MNIST图像分类，深度学习的入门任务。

用 TFlearn 执行：

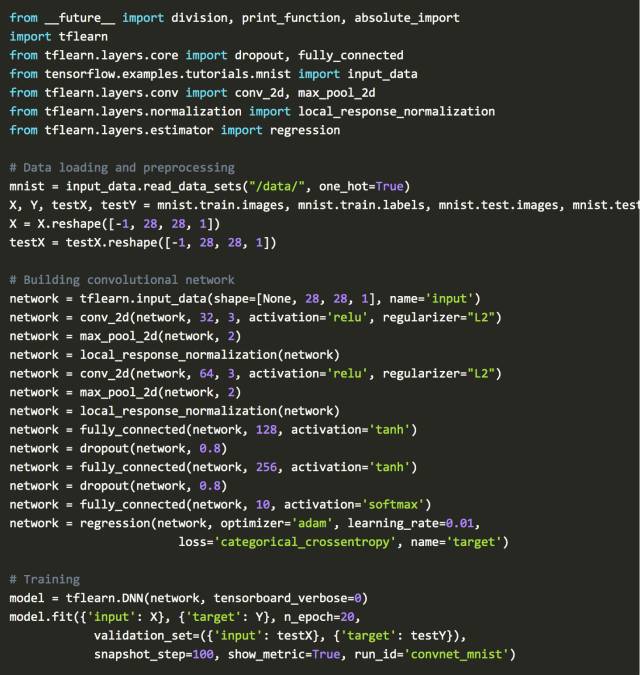
如您在TFlearn示例中所看到的，深度学习的主要逻辑仍然类似于Rosenblatt的感知器。不使用二进制Heaviside step function，今天的网络大多使用Relu activition。在卷积神经网络的最后一层，损失等于categorical_crossentropy。这是勒让德最小二乘法的演变，是多类别的逻辑回归。优化器adam起源于 Debye 梯度下降的工作。 Tikhonov的正则化概念以停用层和正则化函数的形式得到广泛实施。