
看完Andrew Ng老师的机器学习公开课后,对于逻辑回归部分,打算写篇学习笔记记录总结一下,也和大家共同分享。
1
基本思能
逻辑回归(Logistic Regression)和线性回归(Linear Regression)的模型和原理是相似的(哈哈,给我的感觉就像是街霸游戏里的Ryu和Ken),按照我的理解,算法大致可以分为以下步骤:
(1)构造一个合适的预测函数,假设记为h函数。该函数就是我们需要找的分类函数,它用来预测输入数据的判断结果。这个过程非常关键,需要对数据有一定的了解或分析,知道或者猜测预测函数的“大概”形式(走势),比如是线性函数还是非线性函数。(例如y=x,y=x2,y=x3…… 等形式的函数)
(2)构造一个损失函数(loss function)并合成一个代价函数(cost function)。损失函数是表示每一个样本上,预测的输出h与训练数据类别(即真实值)y之间的偏差,可以是二者之间的差(h-y),也可以是(h-y)2(貌似这种常用一点,避免了可能出现负数的情况)或者是其他的形式。综合考虑所有训练数据的“损失”,将其求和或者求平均,就变成了代价函数,记为J(θ)函数(这里的参数θ是指预测函数里面的系数)
(3)寻找代价函数最小值并确定参数。显然,我们希望J(θ)函数的值越小越好,因为这表示我们预测的和实际值越小了,预测函数的表现效果就越好,所以这一步需要做的是找到J(θ)函数的最小值。找函数的最小值有不同的方法,这里要提到的是梯度下降法(Gradient Descent),当然也有其他优秀的算法。
2
推导过程
1
构造预测函数
逻辑回归是一种分类方法,用于两分类问题(即输出只有两种,表示为0和1)。根据上面步骤,需要先找到一个预测函数hθ(x),在这里,我们假设是线性边界的情况,表示形式为:

因为逻辑回归的输出必须是两个值,所以要利用Logistic函数(或称为Sigmoid函数),把输出控制在0到1之间,函数形式为:
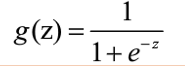
它的函数图像为:
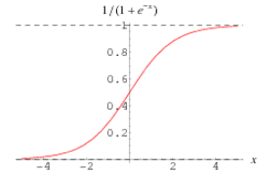
结合这两个函数,我们可以得到:
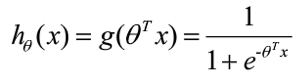
好了,到了这里我们已经定义了一个预测函数,应当注意,hθ(x)的输出值的含义是:它表示结果取1的概率。
2
构造损失函数和代价函数
按照直观思想,或是参照线性回归的代价函数,我们可以写出以下的代价函数:
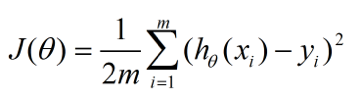
这个代价函数在线性回归里表现的很好,但是用于逻辑回归的话,会变成参数θ的非凸函数。也就是说,假如我们把用在线性回归那一套用在逻辑回归上的话,那么可能会出现下面的情况:
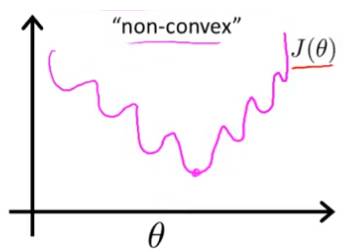
即函数会出现多个局部最优解,这样的函数就是非凸函数。显然,如果我们使用梯度下降法求解的话,往往不能保证它能收敛到全局最小值(因为算法终止条件是导数为0或接近0)。相应地,我们希望代价函数可以是一个凸函数,图像是这样的:
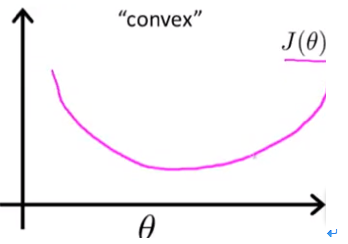
这样一来,我们一旦使用梯度下降法的时候就可以保证能收敛到全局最优解了。之所以会出现非凸函数的问题,是因为在逻辑回归里引入了Sigmoid函数,但它作用在上面的那个J(θ)后,就会出现多个局部最小值的情况。
为了解决这个问题,在极大似然法的基础上,人们提出了运用在逻辑回归的损失函数是:
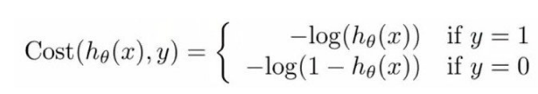
整合成一个式子就是:
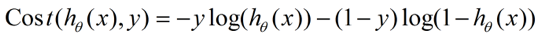
所以最后代价函数的形式是:

为了帮助理解这个cost函数,我们使用Python的matplotlib画一下两种情况的相关图像。
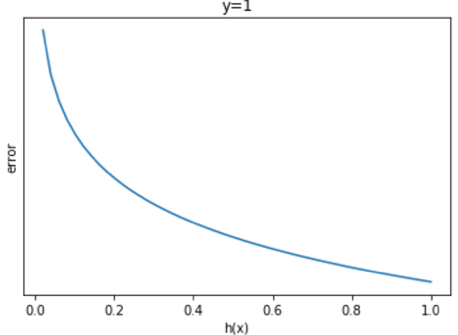
y=1时:

y=0时:
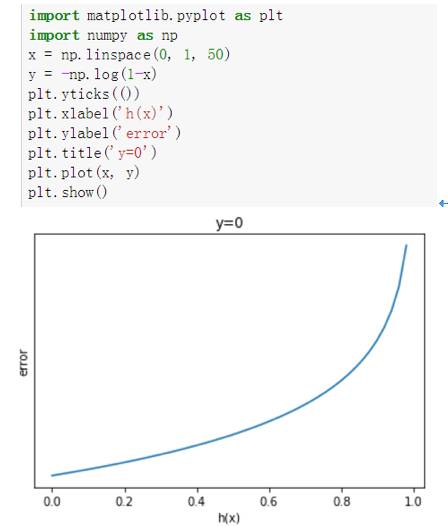
由此我们可以看出,无论是y=0还是y=1的情况,当我们的预测值越接近真实值时,误差会越来越小,当离真实值越远时,误差便越来越大,趋于无穷。结合图像一起看,应该不难理解这个函数了。
3
求解代价函数最小值和参数
在这里,我们用到的是梯度下降法。我们这里只讨论系数是一维的情况,主要是考虑到比较容易理解,也容易用图像表达出来。其实,假如系数是多维的话,核心的思想也是一样的,说白了就是求得导数(多维时就是偏导数)为0(或者设置一个阈值接近0)即可。
接下来就来具体讨论一下。
首先看一下梯度下降法的模式,它的本尊长这样:
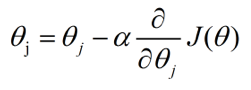
其中θ是我们要求解的系数,α是学习步长。接下来看一下为什么可以用这一条公式来求解最小值(假设此时代价函数已经是凸函数)。
上面说过,我们只讨论最简单的一种情况,即一维系数。我们分两种情况来看一下。
第一种情况,假设我们的θ初始值大于最优解,那么我们可以得到这样的图像:
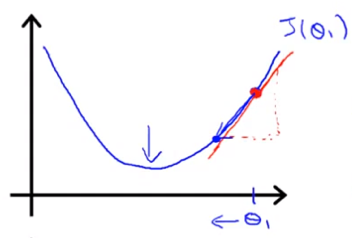
这张图像很好地解释了这个公式的可行性:如果此时的θ在最优解的右边,我们对其进行求导,显然此刻导数为正,那么根据上面的公式,就会减小θ,使其向最优解的方向靠拢。
第二种情况,θ初始值小于最优解,那么我们可以得到这样的图像:
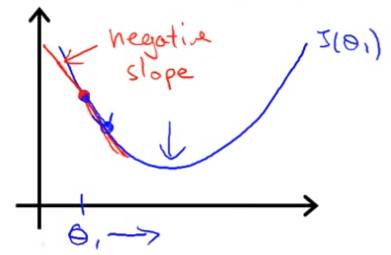
此时的θ在最优解的左边,我们对其进行求导,显然此刻导数为负,那么根据公式,就会增大θ,使其向最优解的方向靠拢。
当然,严格来讲还有第三种,就是我们初始化参数的时候,可以刚刚好满足了我们的要求,然而这个通常不大可能,运气得多好啊,哈哈。。。
所以,这就是梯度下降法的核心思想(看到这里有没有感觉其实也不是很难),我们接下来把它运用到逻辑回归的代价函数里,可以得到这样一个式子:
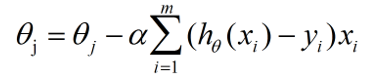
这就是逻辑回归中梯度下降更新系数θ的公式了。
写到这里已经快接近尾声了,在梯度下降法中,还要一点点小问题,就是关于步长α的取值,需要注意的是,当α过大时,可能会不小心就错过了最优解,因为步子迈得大了;α过小时,算法在收敛上会变慢,因为每次只前进那么一点点。所以这个貌似要看经验,并且一般都会试一下好几个不同的步长α来检验算法,避免偶然性。
对于梯度下降而言,因为每次要涉及计算到全部的样本,一旦你的样本数多,拟合的参数多,并且步长设置的也小了一点,那么算法会计算很久。于是现在也有其他的算法用于计算类似的问题,各位小伙伴有兴趣也可以了解一下。
3
小结
这一篇介绍了逻辑回归背后的数学原理,篇幅比较长,可能读起来会比较久,因为大多是公式和原理,所以需要慢慢看,仔细理解。当然,里面还是省略了一些更为仔细的推导部分,主要是导数(偏导数)推导方面的,但基本不会影响到理解这个算法的数学原理。另外,可能有些地方写得还不够透彻,或者写得还不够好,又或者是有出现错误的地方,请大家能多多包涵,多多指教,共同学习,共同进步!

















)


