
本节开始,我们一起来学习线性代数的有关知识,首节我们从解方程谈起,学习线性代数的应用之一就是求解复杂方程问题,本节核心之一即为从行图像与列图像的角度解方程。
2.1 二维的行图像
我们首先通过一个例子来从行图像角度求解方程:

我们首先按行将方程写为矩阵形式:
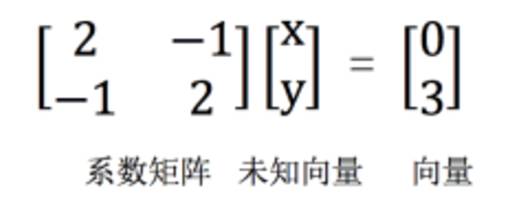
系数矩阵(A):将方程系数按行提取出来,构成一个矩阵。
未知向量(x):将方程未知数提取出来,按列构成一个向量。
向量(b):将等号右侧结果按列提取,构成一个向量。
接下来我们通过行图像来求解这个方程:
所谓行图像,就是在系数矩阵上,一次取一行构成方程,在坐标系上作图。和我们在初等数学中学习的作图求解方程的过程无异。
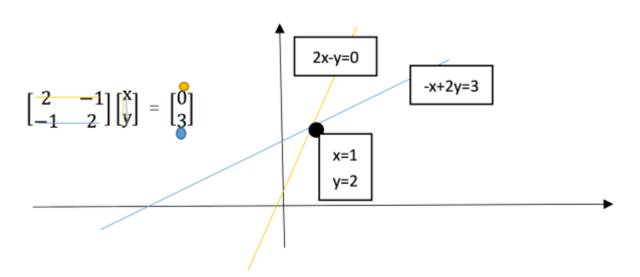
2.2 二维的列图像

接下来我们使用列图像求解此方程:
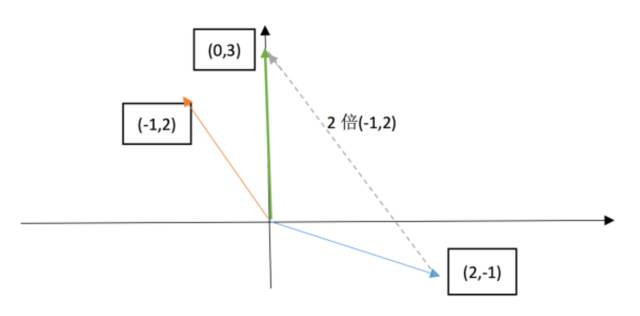
即寻找合适的 x,y 使得 x 倍的(2,-1) + y 倍的(-1,2)得到最终的向量(0,3)。很明显能看出来,1 倍(2,-1) + 2 倍(-1,2)即满足条件。
反映在图像上,明显结果正确。

3.1 高维行图像


如果绘制行图像,很明显这是一个三个平面相交得到一点,我们想直接看出这个点的性质可谓是难上加难。
比较靠谱的思路是先联立其中两个平面,使其相 交于一条直线,在研究这条直线与平面相交于哪个点,最后得到点坐标即为方程 的解。
这个求解过程对于三维来说或许还算合理,那四维呢?五维甚至更高维数呢?直观上很难直接绘制更高维数的图像,这种行图像受到的限制也越来越多。
3.2 高维列图像

左侧是线性组合,右侧是合适的线性组合组成的结果,这样一来思路就清晰多了,“寻找线性组合”成为了解题关键。

很明显这道题是一个特例,我们只需要取 x = 0,y = 0,z = 1。就得到了结果,这在行图像之中并不明显。
当然,之所以我们更推荐使用列图像求解方程, 是因为这是一种更系统的求解方法,即寻找线性组合,而不用绘制每个行方程的图像之后寻找那个很难看出来的点。
另外一个优势在于,如果我们改变最后的结果 b,例如本题中,
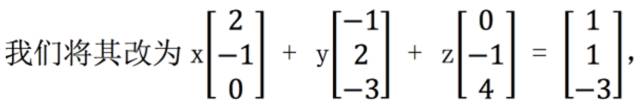
那么我们 2 −1 1 0 −3 4 −3 就重新寻找一个线性组合就够了,但是如果我们使用的是行图像呢?那意味着我 们要完全重画三个平面图像,就简便性来讲,两种方法高下立判。
另外,还要注意的一点是对任意的 b 是不是都能求解 Ax = b 这个矩阵方程呢? 也就是对 3*3 的系数矩阵 A,其列的线性组合是不是都可以覆盖整个三维空间呢?
对于我们举的这个例子来说,一定可以,还有我们上面 2*2 的那个例子,也可以 覆盖整个平面,但是有一些矩阵就是不行的。
比如三个列向量本身就构成了一个 平面,那么这样的三个向量组合成的向量只能活动在这个平面上,肯定无法覆盖 2 −1 1 一个三维空间,

这三个向量就构成了一个平面。

3.3 矩阵乘法

希望对大家有帮助~







)
)










