推荐阅读时间8min~13min

主要内容：通俗理解激活函数，主要来自我在学习会的slides，讲解了激活函数的非线性能力和组合特征的作用

下面我分别对激活函数的两个作用进行解释。

1

加入非线性因素，解决非线性问题

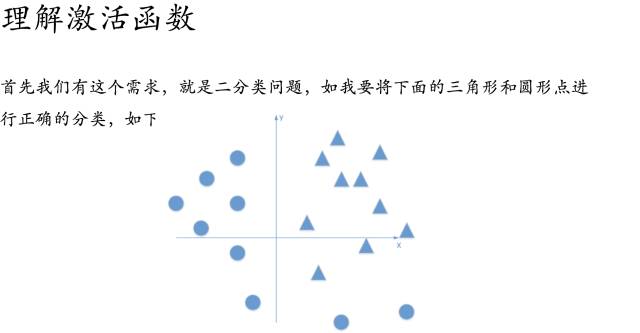
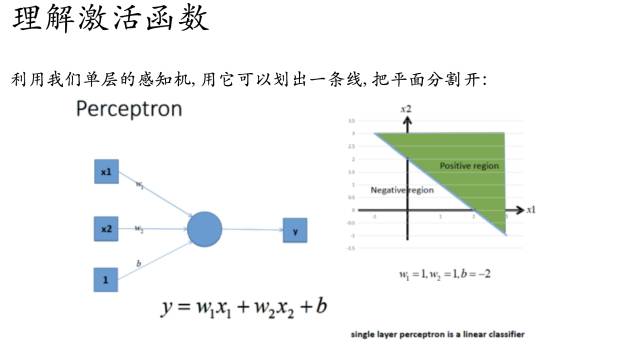
好吧，很容易能够看出，我给出的样本点根本不是线性可分的，一个感知器无论得到的直线怎么动，都不可能完全正确的将三角形与圆形区分出来，那么我们很容易想到用多个感知器来进行组合，以便获得更大的分类问题，好的，下面我们上图，看是否可行

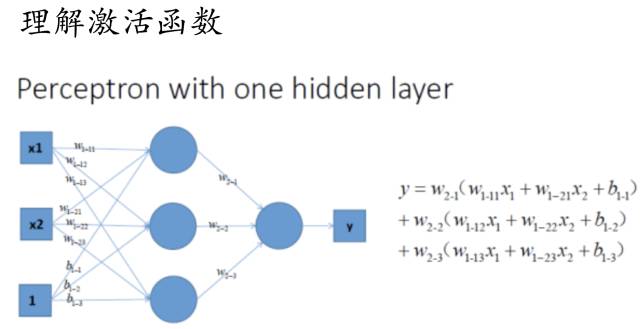
好的，我们已经得到了多感知器分类器了，那么它的分类能力是否强大到能将非线性数据点正确分类开呢~我们来分析一下：

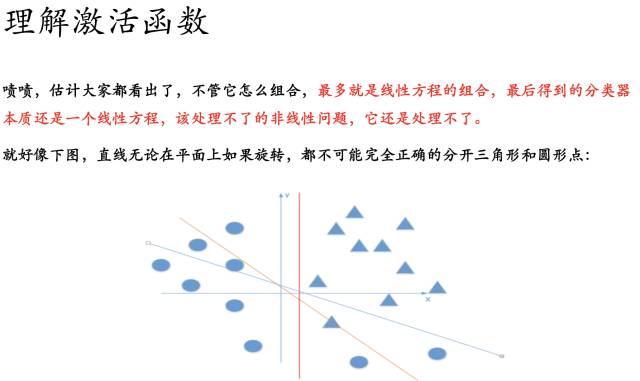
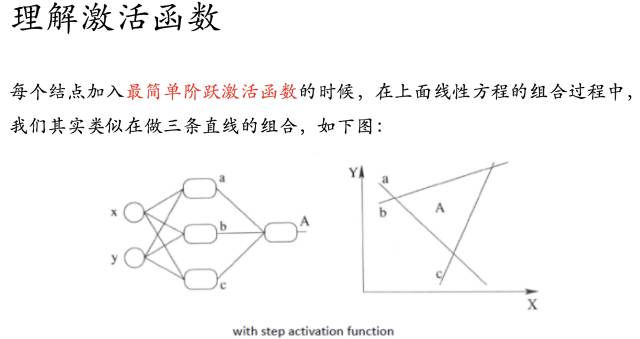
如果我们的每一个结点加入了阶跃函数作为激活函数的话，就是上图描述的

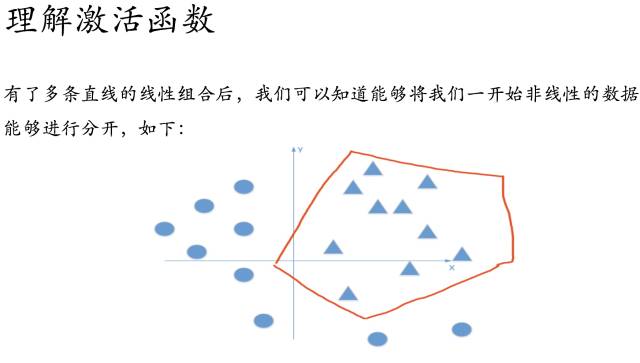
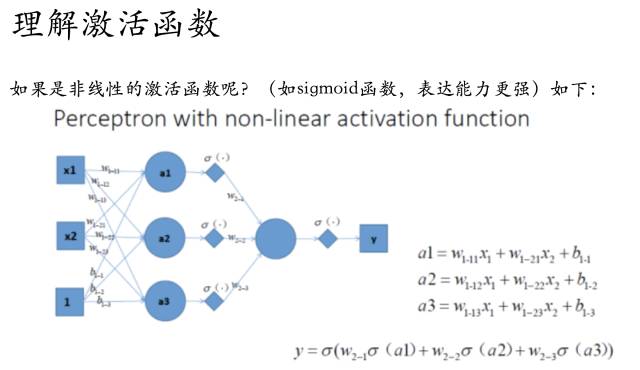
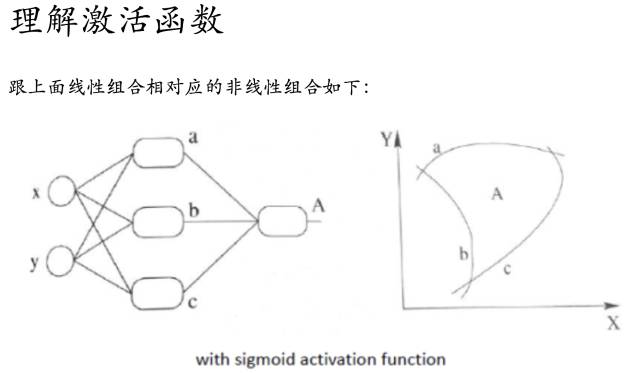
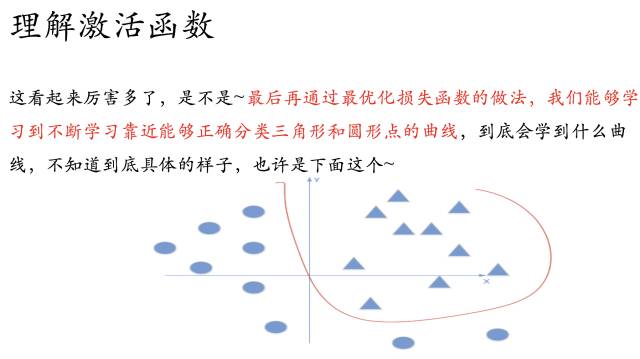
那么随着不断训练优化，我们也就能够解决非线性的问题了~

所以到这里为止，我们就解释了这个观点，加入激活函数是用来加入非线性因素的，解决线性模型所不能解决的问题。

下面我来讲解另一个作用

2

 激活函数可以用来组合训练数据的特征，特征的充分组合

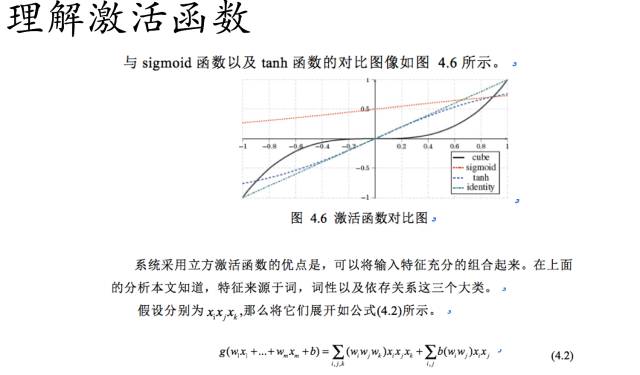
我们可以通过上图可以看出，立方激活函数已经将输入的特征进行相互组合了。

通过泰勒展开，我们可以看到，我们已经构造出立方激活函数的形式了。

于是我们可以总结如下：

3

总结

这就把原来需要领域知识的专家对特征进行组合的情况，在激活函数运算后，其实也能够起到特征组合的作用。（只要激活函数中有能够泰勒展开的函数，就可能起到特征组合的作用）

这也许能给我们一些思考。