
前文介绍了在知道符号序列后用viterbi算法求解最可能路径。本文介绍了如何使用前向算法和后向算法计算符号序列的全概率。
如果一个符号序列中每个符号所对应的状态是已知的,那么这个符号序列出现的概率是容易计算的:
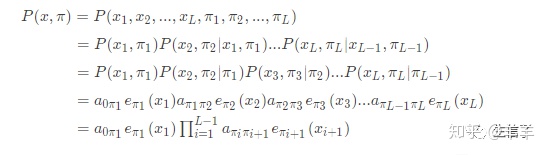
但是,如果一个符号序列中每个符号所对应的状态未知时,该怎么求取这条序列的概率呢?我们知道:
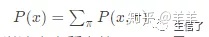
如果我们用穷举法求出所有的P(x,π)是不现实的,因为随着序列长度的增长,所有可能的路径的数目是指数增长的。这个时候,我们可以再次借助动态规划来求取。
有两种方法,前向法和后向法。二者的区别是前向法是从序列头部开始计算,逐步向序列尾部推进;而后向法是从序列尾部开始计算,逐步向序列头部推进。
前向法
定义:
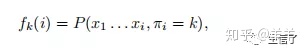
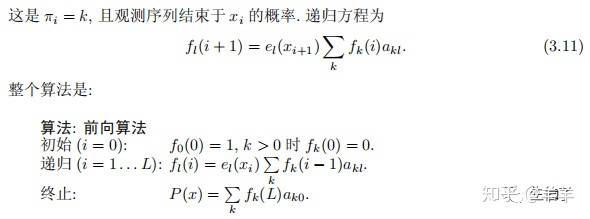
后向法
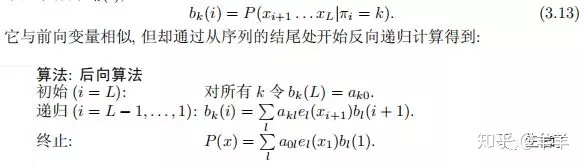
解决下溢的问题
与《序列比对(十)viterbi算法求解最可能路径》一文中的viterbi算法相似,前向法和后向法也都涉及到下溢的问题。由于递归公式中涉及到加法,所以不能像《序列比对(十)viterbi算法求解最可能路径》中简单使用log变换。《生物序列分析》一书中给出了两种解决方法:
一是近似的log变换

二是使用一组缩放因子

实现代码和效果
下面的代码首先随机生成一个状态序列和相应的符号序列,然后根据前向法和后向法来计算符号序列的全概率。本文采用缩放因子来解决下溢的潜在问题。这样做有一个好处,就是此时所有缩放因子的乘积就等于P(x)。
效果如下:
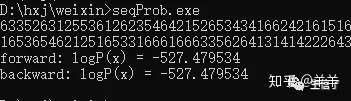
具体代码:
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include <math.h>
//#define MIN_LOG_VALUE -15
//#define SAFE_EXP(x) ((x) < MIN_LOG_VALUE ? 0 : exp(x))typedef char State;
typedef char Result;
State state[] = {'F', 'L'}; // 所有的可能状态
Result result[] = {'1', '2', '3', '4', '5', '6'}; // 所有的可能符号
double init[] = {0.9, 0.1}; // 初始状态的概率向量
double emission[][6] = { // 发射矩阵:行对应着状态,列对应着符号1.0/6, 1.0/6, 1.0/6, 1.0/6, 1.0/6, 1.0/6,0.1, 0.1, 0.1, 0.1, 0.1, 0.5
};
double trans[][2] = { // 转移矩阵:行和列都是状态0.95, 0.05,0.1, 0.9
};
const int nstate = 2;
const int nresult = 6;State* rst; // 一串随机状态序列
Result* rres; // 一串随机符号序列
double** fscore; // 前向算法的得分矩阵
double** bscore; // 后向算法的得分矩阵
double* scale; // 缩放因子向量
double logScaleSum;struct Unit {double v;int *p;int size;
};
typedef struct Unit* pUnit;int random(double* prob, const int n);
void randSeq(State* st, Result* res, const int n);
int getResultIndex(Result r);
void printResult(Result* res, const int n);
double forward(const int n);
double backward(const int n);int main(void) {int i;int n = 300;if ((rst = (State*) malloc(sizeof(State) * n)) == NULL || (rres = (Result*) malloc(sizeof(Result) * n)) == NULL || (scale = (double*) malloc(sizeof(double) * n)) == NULL || (fscore = (double**) malloc(sizeof(double*) * nstate)) == NULL || (bscore = (double**) malloc(sizeof(double*) * nstate)) == NULL) {fputs("Error: out of space!n", stderr);exit(1);}for (i = 0; i < nstate; i++) {if ((fscore[i] = (double*) malloc(sizeof(double) * n)) == NULL || (bscore[i] = (double*) malloc(sizeof(double) * n)) == NULL) {fputs("Error: out of space!n", stderr);exit(1);}}randSeq(rst, rres, n);printResult(rres, n);forward(n);backward(n);free(rst);free(rres);free(scale);free(fscore);free(bscore);
}// 根据一个概率向量从0到n-1随机抽取一个数
int random(double* prob, const int n) {int i;double p = rand() / 1.0 / (RAND_MAX + 1);for (i = 0; i < n - 1; i++) {if (p <= prob[i])break;p -= prob[i];}return i;
}// 根据转移矩阵和发射矩阵生成一串随机状态和符号
void randSeq(State* st, Result* res, const int n) {int i, ls, lr;srand((unsigned int) time(NULL));ls = random(init, nstate);lr = random(emission[ls], nresult);st[0] = state[ls];res[0] = result[lr];for (i = 1; i < n; i++) {ls = random(trans[ls], nstate);lr = random(emission[ls], nresult);st[i] = state[ls];res[i] = result[lr];}
}int getResultIndex(Result r) {return r - result[0];
}// 前向算法计算P(x)
double forward(const int n) {int i, l, k, idx;double logpx;// 缩放因子向量初始化for (i = 0; i < n; i++)scale[i] = 0;// 计算第0列分值idx = getResultIndex(rres[0]);for (l = 0; l < nstate; l++) {fscore[l][0] = emission[l][idx] * init[l];scale[0] += fscore[l][0];}for (l = 0; l < nstate; l++)fscore[l][0] /= scale[0];// 计算从第1列开始的各列分值for (i = 1; i < n; i++) {idx = getResultIndex(rres[i]);for (l = 0; l < nstate; l++) {fscore[l][i] = 0;for (k = 0; k < nstate; k++) {fscore[l][i] += fscore[k][i - 1] * trans[k][l];}fscore[l][i] *= emission[l][idx];scale[i] += fscore[l][i];}for (l = 0; l < nstate; l++)fscore[l][i] /= scale[i];}// P(x) = product(scale)// P(x)就是缩放因子向量所有元素的乘积logpx = 0;for (i = 0; i < n; i++)logpx += log(scale[i]);printf("forward: logP(x) = %fn", logpx);logScaleSum = logpx;
/*for (l = 0; l < nstate; l++) {for (i = 0; i < n; i++)printf("%f ", fscore[l][i]);printf("n");}
*/return exp(logpx);
}// 后向算法计算P(x)
// backward算法中使用的缩放因子和forward中的一样
double backward(const int n) {int i, l, k, idx;double tx, logpx;// 计算最后一列分值for (l = 0; l < nstate; l++)bscore[l][n - 1] = 1 / scale[n - 1];// 计算从第n - 2列开始的各列分值for (i = n - 2; i >= 0; i--) {idx = getResultIndex(rres[i + 1]);for (k = 0; k < nstate; k++) {bscore[k][i] = 0;for (l = 0; l < nstate; l++) {bscore[k][i] += bscore[l][i + 1] * trans[k][l] * emission[l][idx];}}for (l = 0; l < nstate; l++)bscore[l][i] /= scale[i];}// 计算P(x)tx = 0;idx = getResultIndex(rres[0]);for (l = 0; l < nstate; l++)tx += init[l] * emission[l][idx] * bscore[l][0];logpx = log(tx) + logScaleSum;printf("backward: logP(x) = %fn", logpx);
/*for (l = 0; l < nstate; l++) {for (i = 0; i < n; i++)printf("%f ", bscore[l][i]);printf("n");}
*/return exp(logpx);
}void printResult(Result* res, const int n) {int i;for (i = 0; i < n; i++)printf("%c", res[i]);printf("n");
}(公众号:生信了)
















)


