nuke中的表达式节点对于大多数人来说有点神秘，但它非常强大。通常它通过简单的if / else语句修补数据，但在这里我们将从最基本的原则，到一些长期被遗忘的高中数学做一些简单的技巧，最后把它们融合在一起。

第一步

创建Constant节点，并附加表达式节点。如果是默认状态，它什么都不做。您可以看到底部有4个通道的字段（rgba），顶部有一些基本变量的空间，我们稍后会介绍。

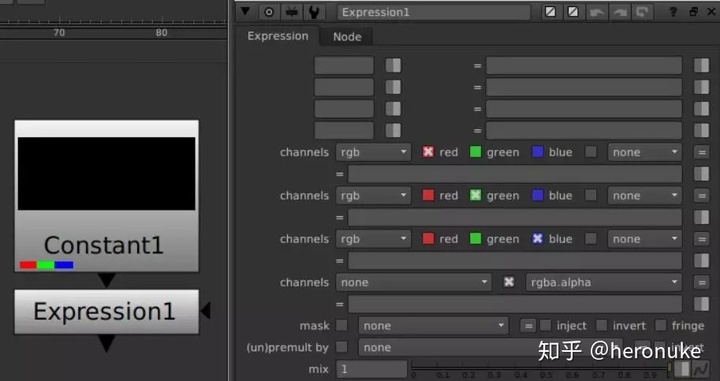
所以，简单的表达式开始。在第一个通道表达式槽中输入“1”。上面的复选框说明要操作的通道，默认情况下它只是红色通道。按Enter键，您将看到整个图像变为红色。

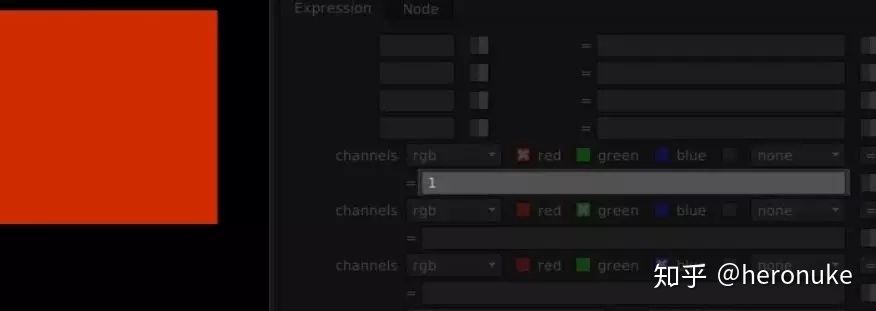
我们在这里所做的就是让每个像素的红色通道数值为1.非常简单。

渐变

这次，输入'x'，点击回车。根据观察者的不同，你要么仍然看到红色，要么看到一个超级红色。将光标悬停在查看器中，查看颜色值。您可以看到我们将每个像素的x坐标直接映射到红色通道。

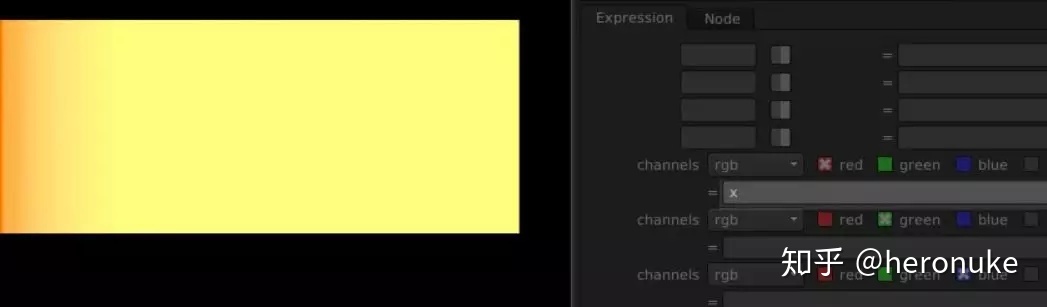
为了更好地看到这个渐变，我们可以重新映射这些值，使它们保持在0和1之间。为此，我们需要将x坐标除以图像宽度。输入：x / width

一个漂亮的水平渐变就出现了。但如果我们想要垂直渐变怎么办？

输入：y / height

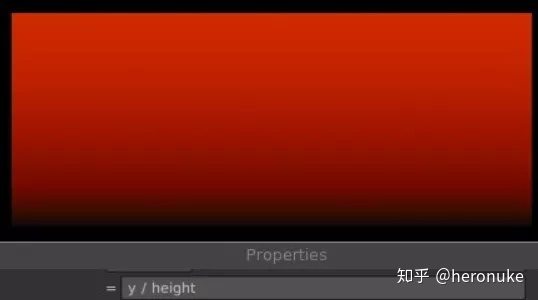
如果要反转渐变，请从1减去它：1 - (y / height)

现在，如果我们想要重复线条怎么办？

把你的思维转回到高中数学，以及sin（）的图形是什么样的。如果我们给它一个永远增加的数字，它将介于-1和1之间。让我们看看它是什么样的：sin(x)

如果将鼠标悬停在查看器上，你将看到值确实在预测的-1和1之间。为了规范化，我们添加1，使其在0和2之间：sin(x) + 1

然后将整个事物除以2，给出0到1之间的值：( sin(x) + 1 ) / 2

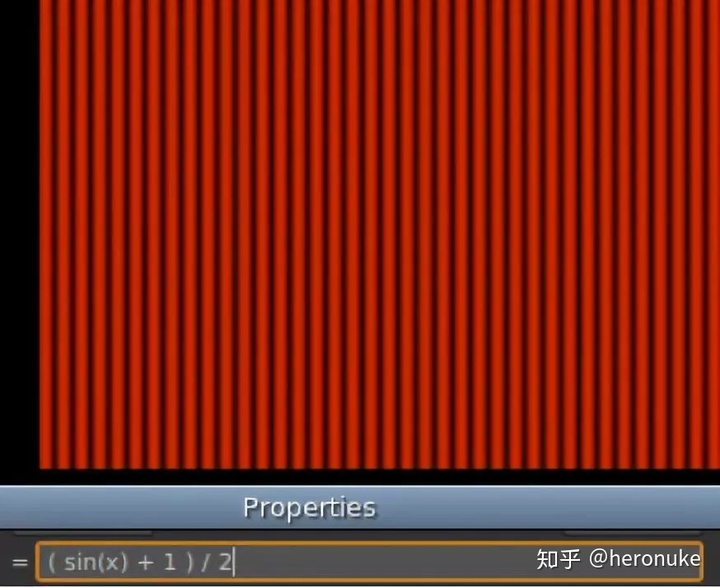
为了制作更宽的线，我们希望x以较慢的速率增加，所以我们将它除以某个值：( sin(x / 4 ) + 1 ) / 2

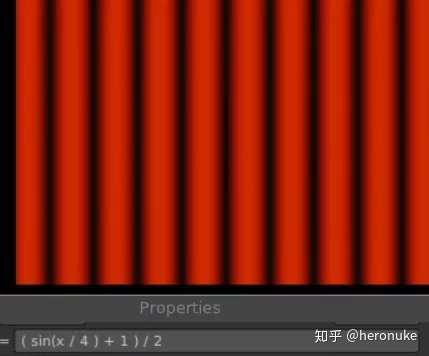
要改变黑色与红色线的比例，我们可以做更多的表达，或者使用Nuke来发挥我们的优势。附加一个Grade节点，并弄乱blackpoint。这将使黑色区域变得越来越大。

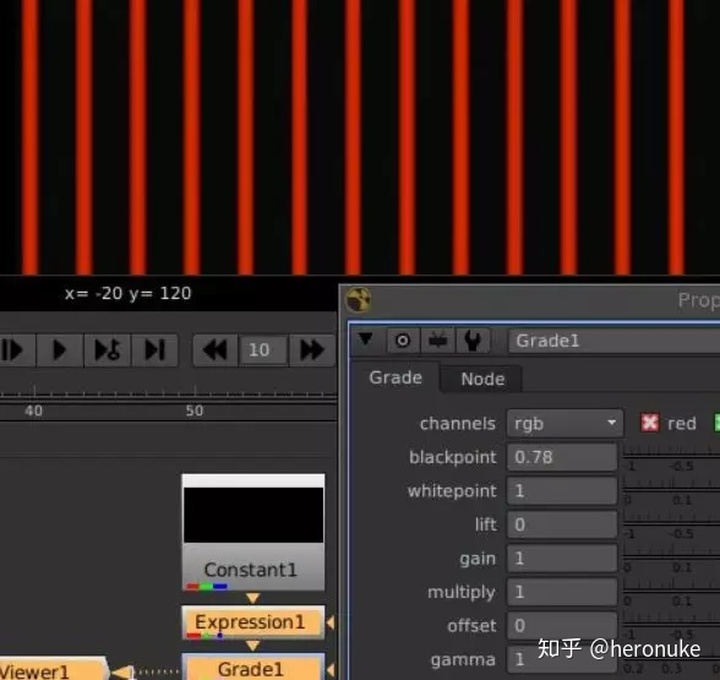
径向渐变

新的挑战。如果我们想测量每个像素与原点的距离怎么办？再回到高中数学; 我们有一个直角三角形的两边，我们想测量第三条边。我们可以做“A平方加上B平方”的事情（确保你正在查看表达式节点）：sqrt(x * x + y * y )

将鼠标悬停在图像上方，您会看到左下角的红色值为0，当您离开（0,0）时，数字会平滑增加。这是一个径向渐变！

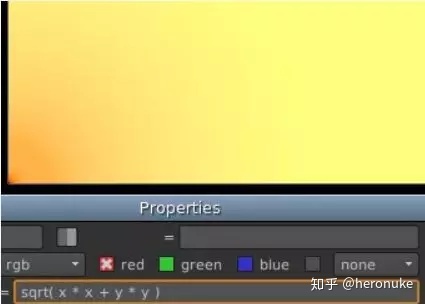
要反转它，从数字中减去它，这个数字将是渐变的宽度：300 - sqrt(x * x + y * y )

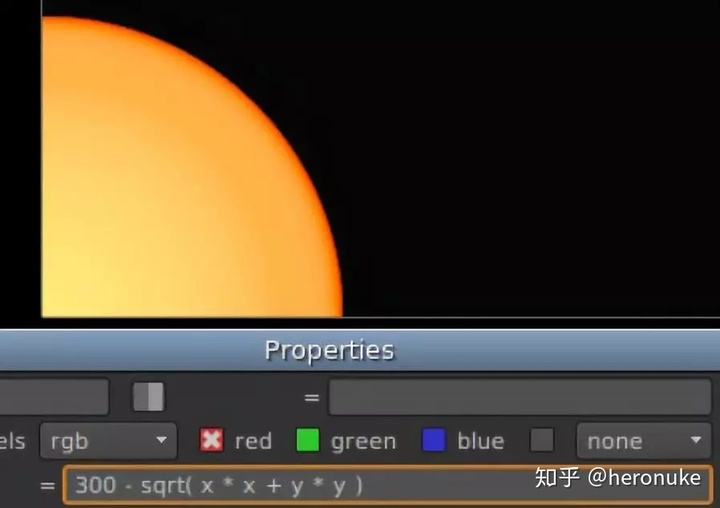
并将其标准化为0到1之间，将整个表达式除以相同的数字：(300 - sqrt( x * x + y * y ) ) / 300

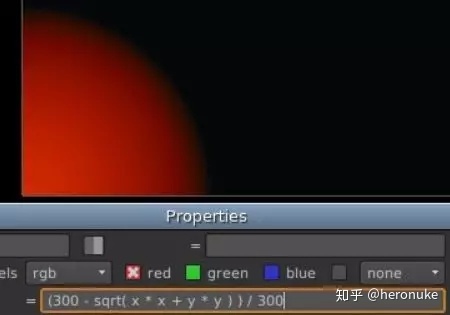
径向环

我们之前可以做类似的技巧; 取出结果，并将其提供给sin（）：sin(sqrt(x * x + y * y ))

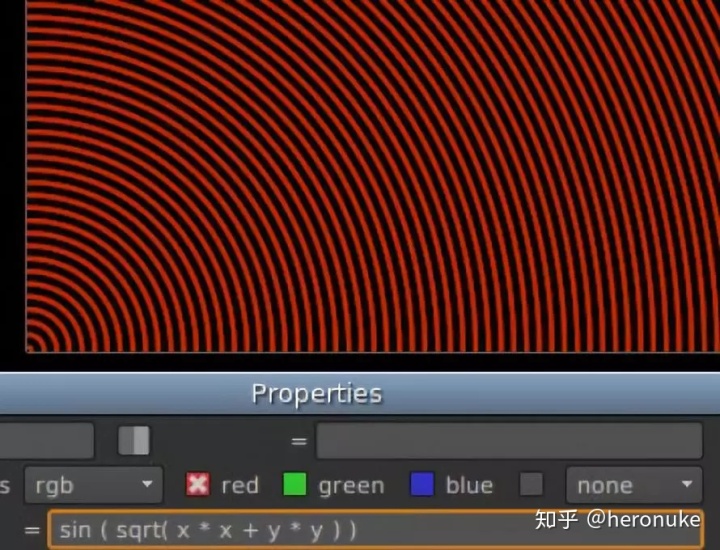
出现了一个同心环！要缩放，在内部除以一个数使距离增加更慢：sin(sqrt(x * x + y * y ) / 4)

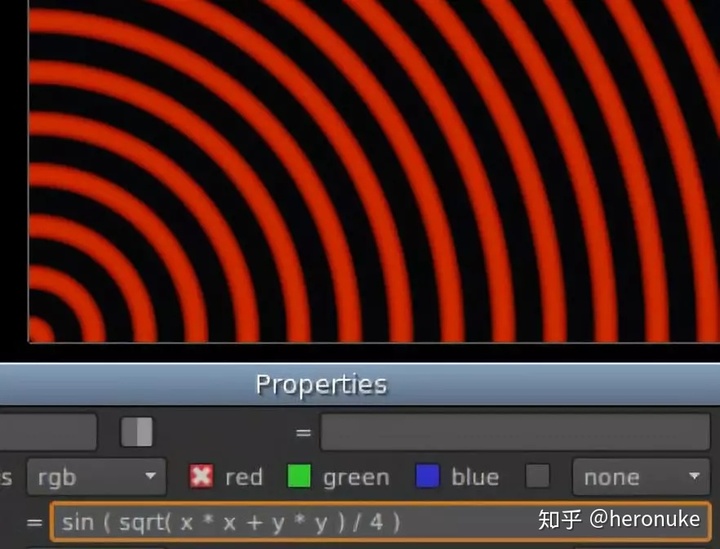
再次查看Grade节点，并调整黑色与红色的比率。

更好的控制

如果你想移动这些环的中心点怎么办？基本上，你希望测量的距离不是从（0,0）开始，而是从另一个点开始。您可以从x和y值中减去该值。例如，让我们将中心点移动到（300,50）：sin(sqrt((x-300) * (x-300) + (y-50) * (y-50) ) / 4)

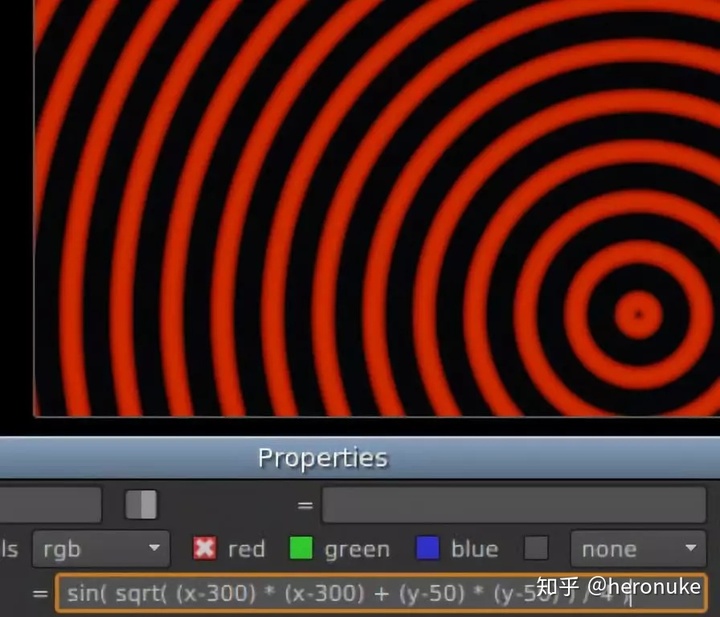
这很有效，但很难更新。有一个可视化工具让我们拖动它会更好。Nuke中可以这样做。在属性窗格中，右键单击文本字段以外的任何位置，然后选择“管理用户旋钮...”。

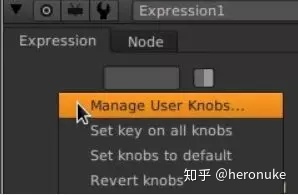
点击添加，选择'2d Position Knob ...'，将其命名为'center'。点击确定然后完成。

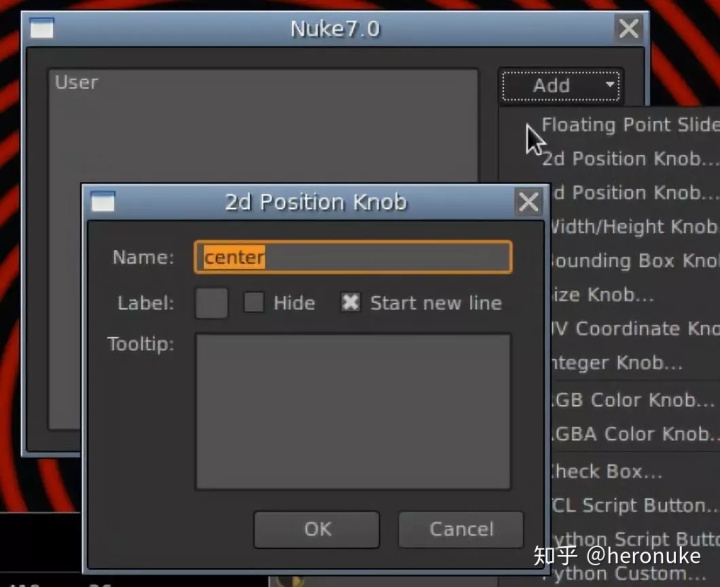
你会看到你有一个新的'用户'标签，带有x和y值。在查看器中，您将在左下方看到“中心”Gizmo，您可以将其拖动到图像上的任何位置，并查看值更新。

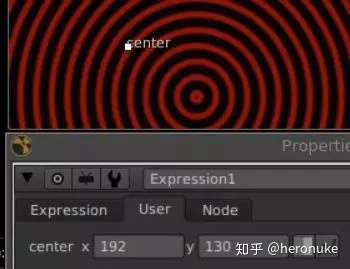
要在表达式中使用它，只需使用center.x和center.y：sin(sqrt((x-center.x) * (x-center.x) + (y-center.y) * (y-center.y) ) / 4)

虽然我确信你会因为记住勾股定理而感到兴奋，但是在Nuke中有一个更简单的方法来计算斜边：sin(hypot(x-center.x, y-center.y ) / 4)

让我们用滑块替换该比例倍增器。再次右键单击表达式，“管理用户旋钮”，这次添加一个名为“size”的浮点滑块，将其最小值设置为0.1，最大值设置为20.将表达式更改为：sin(hypot(x-center.x, y-center.y ) / size)

更改尺寸滑块，移动中心点，查看环跟随。

好的，这是同心环。径向射线又会怎么样？

径向光线

再回到高中数学！还记得sin / cos / tan和直角三角形之间的关系吗？在下图中，tan是对边除以邻边的比率。

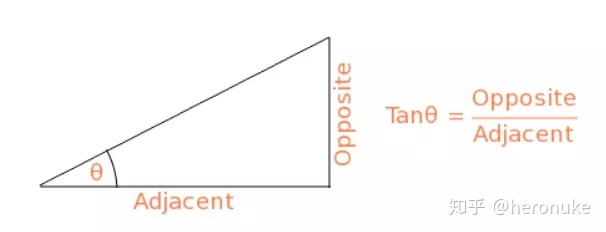
我们可以将对立和相邻视为x和y，并使用正切来获得圆弧或角度。将这些数字插入：atan(x - center.x, y - center.y)

你会得到一个奇怪的渐变，一边是渐变色，另一边是黑色。如果将光标悬停在图像上并查看值，您将看到黑色区域实际上是负值。用光标在中心点周围跟踪一个圆圈，注意值从底部的-1.24到顶部的0，再到底部的1.24。基本上，它描绘出一个圆圈。

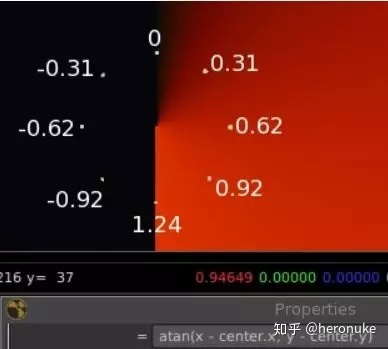
我们可以重置圆的范围，使其从0变为1：(atan(x - center.x, y - center.y) + 3.14 ) / 2.48

或者从之前做出诀窍得到径向线：sin( atan(x - center.x, y - center.y) )

对于同心线，问题是输入增加太快，所以我们将它减小以减慢它，给我们更宽的线。在这里，相加太慢，所以我们将输入乘以我们的size属性以获得更多行：sin( atan(x - center.x, y - center.y) * size)

让我们添加一个偏移量，以便我们可以根据需要旋转它们。添加一个名为'offset'的浮点滑块，给它一个0到50的范围，并将其添加到atan结果，但在乘以size之前：sin( ( atan(x - center.x, y - center.y) + offset) * size)

滑动滑块，看光线旋转。

今天给大家介绍了一些表达式，明天，我将会给大家介绍如何应用这些表达式以及P_matte（一个有用的小插件）的工作原理。