隐含马尔可夫模型（Hidden Markov Model）

隐含马尔可夫模型并不是俄罗斯数学家马尔可夫发明的，而是美国数学家鲍姆提出的，隐含马尔可夫模型的训练方法（鲍姆-韦尔奇算法）也是以他名字命名的。隐含马尔可夫模型一直被认为是解决大多数自然语言处理问题最为快速、有效的方法。

马尔可夫假设

随机过程中各个状态St的概率分布，只与它的前一个状态St-1有关，即P(St|S1,S2,S3,…,St-1) = P(St|St-1)。

比如，对于天气预报，硬性假定今天的气温只与昨天有关而和前天无关。当然这种假设未必适合所有的应用，但是至少对以前很多不好解决的问题给出了近似解。

马尔可夫链

符合马尔可夫假设的随机过程称为马尔可夫过程，也称为马尔可夫链。

在这个马尔可夫链中，四个圈表示四个状态，每条边表示一个可能的状态转换，边上的权值是转移概率。

隐含马尔可夫链是上述马尔可夫链的一个扩展：任一时刻t的状态St是不可见的。所以观察者没法通过观察到一个状态序列S1,S2,S3,…,ST来推测转移概率等参数。但是隐含马尔可夫模型在每个时刻t会输出一个符号Ot，而且Ot和St相关且仅和St相关。这称为独立输出假设。

隐含马尔可夫模型的结构如下图，其中隐含的状态S1,S2,S3,…是一个典型的马尔可夫链。鲍姆把这种模型称为“隐含”马尔可夫模型。

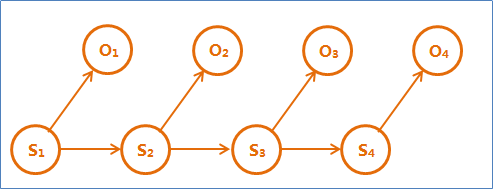
隐含马尔可夫模型的三个基本问题

1、给定一个模型，如何计算某个特定的输出序列的概率？ 

Forward-Backward算法

2、给定一个模型和某个特定的输出序列，如何找到最可能产生这个输出的状态序列？

维特比算法

3、给定足够量的观测数据，如何估计隐含马尔可夫模型的参数？

训练隐含马尔可夫模型更实用的方式是仅仅通过大量观测到的信号O1，O2，O3，….就能推算模型参数的P(St|St-1)和P(Ot|St)的方法（无监督训练算法），其中主要使用鲍姆-韦尔奇算法。 

隐含马尔可夫模型的五元组

HMM是一个五元组（O , Q , O0，A , B）:

1、O:{o1,o2,…,ot}是状态集合，也称为观测序列。

2、Q:{q1,q2,…,qv}是一组输出结果，也称为隐序列。

3、Aij = P(qj|qi)：转移概率分布

4、Bij = P(oj|qi)：发射概率分布

5、O0是初始状态，有些还有终止状态。

维特比算法（Viterbi）

1、简介

维特比算法是一个特殊但应用最广的动态规划算法，它是针对篱笆网络的有向图（Lattice）的最短路径问题而提出的。

凡是使用隐含马尔可夫模型描述的问题都可以用维特比算法来解码，包括今天的数字通信、语音识别、机器翻译、拼音转汉字、分词等。

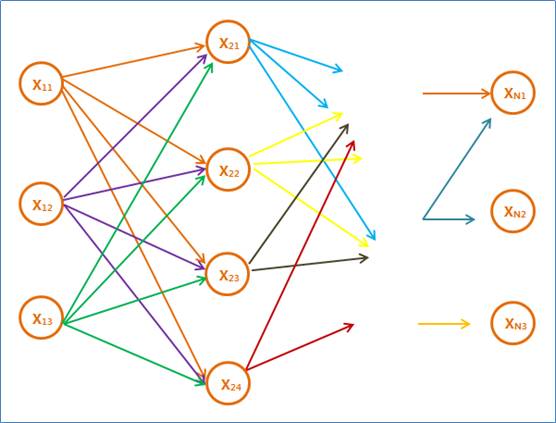
2、维特比算法的基础

1、如果概率最大的路径P（或叫最短路径）经过某个点，比如下图中的X22，那么这条路径上从起始点S到X22的这一段子路径Q，一定是S到X22之间的最短路径。否则，用S到X22的最短路径R替代Q，便构成了一条比P更短的路径，这显然是矛盾的。

2、从S到E的路径必定经过第i时刻的某个状态，假定第i时刻有k个状态，那么如果记录了从S到第i个状态的所有k个节点的最短路径，最终的最短路径必经过其中的一条。这样，在任何时刻，只需要考虑非常有限条最短路径即可。

3、结合上述两点，假定当我们从状态i进入状态i+1时，从S到状态i上各个节点的最短路径已经找到，并且记录在这些节点上，那么在计算从起点S到前一个状态i所有的k个结点的最短路径，以及从这k个节点到Xi+1，j的距离即可。

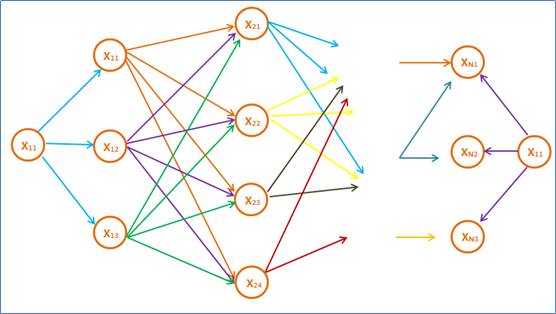
3、维特比算法总结

（1）从点S出发，对于第一个状态X1的各个节点，不妨假定有n1个，计算出S到它们的距离d(S,X1i)，其中X1i代表任意状态1的节点。因为只有一步，所以这些距离都是S到它们各自的最短距离。

（2）对于第二个状态X2的所有节点，要计算出从S到它们的最短距离。对于特点的节点X2i，从S到它的路径可以经过状态1的n1中任何一个节点X1i，对应的路径长度就是d(S,X2i) = d(S,X1i) + d(X1i,X2i)。

由于j有n1种可能性，我们要一一计算，找出最小值。即：d(S,X2i) = minI=1，n1 d(S,X1i) + d(X1i,X2i)

这样对于第二个状态的每个节点，需要n1次乘法计算。假定这个状态有n2个节点，把S这些节点的距离都算一遍，就有O(n1·n2)次计算。

（3）接下来，类似地按照上述方法从第二个状态走到第三个状态，一直走到最后一个状态，就得到了整个网格从头到尾的最短路径。每一步计算的复杂度都和相邻两个状态Si和Si+1各自的节点数目ni，ni+1的乘积成正比，即O(ni·ni+1)

（4）假设这个隐含马尔可夫链中节点最多的状态有D个节点，也就是说整个网格的宽度为D，那么任何一步的复杂度不超过O(D2)，由于网格长度是N，所以整个维特比算法的复杂度是O(N·D2)。

HMM模型+维特比算法实例

1、问题描述

假设连续观察3天的海藻湿度为(Dry,Damp,Soggy),求这三天最可能的天气情况。

2、已知信息

（1）天气只有三类(Sunny,Cloudy,Rainy)，海藻湿度有四类{Dry,Dryish, Damp,Soggy }，而且海藻湿度和天气有一定的关系。

（2）隐藏的状态：Sunny, Cloudy, Rainy;

（3）观察状态序列：{Dry, Damp, Soggy}

（4）初始状态序列：

（5）状态转移矩阵：

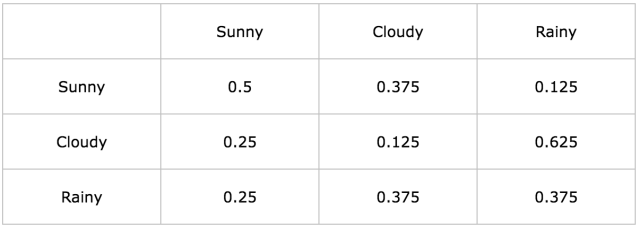
（6）发射矩阵：

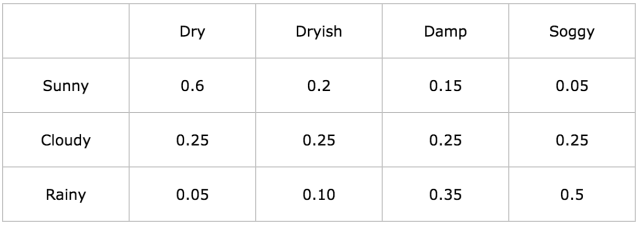
分析

由一阶HMM可知，Day2的天气仅取决于Day1；Day3的天气又只取决于Day2的天气。

计算过程

1、Day1由于是初始状态，我们分别求

P(Day1-Sunny)=0.63*0.6;

P(Day1-Cloudy)=0.17*0.25;

P(Day1-Rain)=0.20*0.05;

Choose max{ P(Day1-Sunny) , P(Day1-Cloudy),P(Day1-Rainy)}, 得到P(Day1-Sunny)最大，得出第1天Sunny的概率最大。

2、Day2的天气又取决于Day1的天气状况，同时也受Day2观察的海藻情况影响。

P(Day2-Sunny)= max{ P(Day1-Sunny)*0.5, P(Day1-Cloudy)*0.25,  P(Day1-Rainy)*0.25} *0.15;

P(Day2-Cloudy)= max{ P(Day1-Sunny)*0.375,  P(Day1-Cloudy)*0.125, P(Day1-Rainy)*0.625} *0.25;

P(Day2-Rainy)= max{ P(Day1-Sunny)*0.125,  P(Day1-Cloudy)*0.625 , P(Day1-Rainy)*0.375} *0.35;

Choosemax{ P(Day2-Sunny) , P(Day2-Cloudy), P(Day2-Rainy)},得到P(Day2-Rainy)最大，得出第2天Rainy的概率最大。

故{Sunny,Rainy}是前两天最大可能的天气序列。

3、Day3的天气又取决于Day2的天气状况，同时也受Day3观察的海藻情况影响。

P(Day3-Sunny)= max{ P(Day2-Sunny)*0.5, P(Day2-Cloudy)*0.25,  P(Day2-Rainy)*0.25} *0.05;

P(Day3-Cloudy)= max{ P(Day2-Sunny)*0.375,  P(Day2-Cloudy)*0.125, P(Day2-Rainy)*0.625} *0.25;

P(Day3-Rainy)= max{ P(Day2-Sunny)*0.125,  P(Day2-Cloudy)*0.625, P(Day2-Rainy)*0.375} *0. 05;

Choosemax{ P(Day3-Sunny) , P(Day3-Cloudy), P(Day3-Rainy)},得到P(Day3-Rainy)最大，得出第3天Rainy的概率最大。故{Sunny,Rainy,Rainy}是这三天最可能的天气序列。

转自：Denise_hzf

https://www.cnblogs.com/Denise-hzf/p/6612212.html