原标题：数学之算法与程序框图

1、算法的定义：广义的算法是指完成某项工作的方法和步骤，现代意义的算法是指可以用计算机来解决的某一类问题的程序和步骤，这些程序或步骤必须是明确和有效的，而且能够在有限步之内完成。

2、流程图的概念：流程图是用一些规定的图形、指向线及简单的文字说明来表示算法几程序结构的一种图形程序．它直观、清晰，便于检查和修改.其中，图框表示各种操作的类型，图框中的文字和符号表示操作的内容，带箭头的流程线(指向线)表示操作的先后次序。

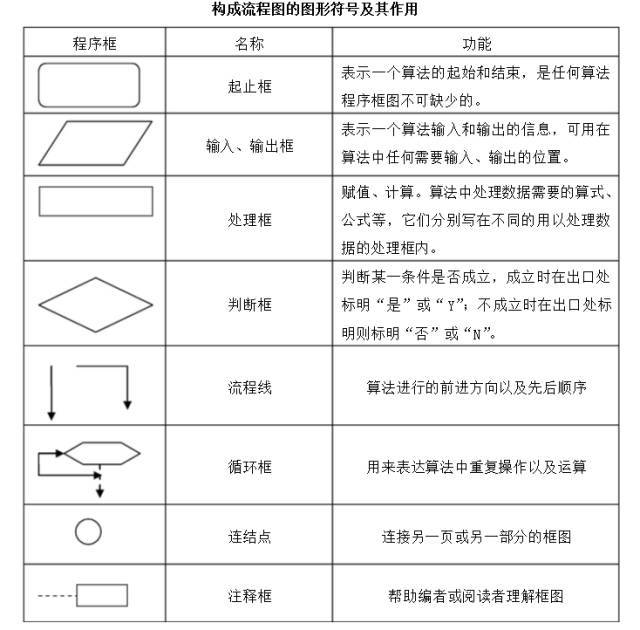
3、规范流程图的表示：

①使用标准的框图符号。

②框图一般按从上到下、从左到右的方向画，流程线要规范。

③除判断框外，大多数框图符号只有一个进入点和一个退出点。

④在图形符号内描述的语言要非常简练、清楚。

4、算法的三种基本逻辑结构：

课本中例题的讲解得出三种基本逻辑结构：顺序结构、条件结构、循环结构。

(1)顺序结构：顺序结构描述的是是最简单的算法结构，语句与语句之间，框与框之间是按从上到下的顺序进行的。

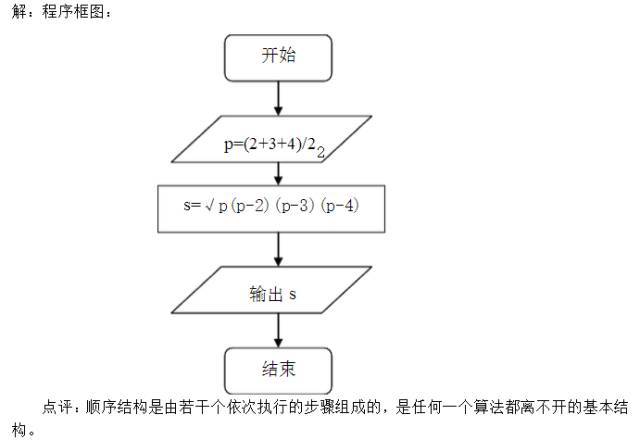
例1：已知一个三角形的三边分别为2、3、4，利用海伦公式设计一个算法，求出它的面积，并画出算法的程序框图。 算法分析：这是一个简单的问题，只需先算出p的值，再将它代入公式，最后输出结果，只用顺序结构就能够表达出算法。

(2)条件结构：根据条件选择执行不同指令的控制结构。 例2：任意给定3个正实数，设计一个算法，判断分别以这3个数为三边边长的三角形是否存在，画出这个算法的程序框图。 算法分析：判断分别以这3个数为三边边长的三角形是否存在，只需要验收这3个数当中任意两个数的和是否大于第3个数，这就需要用到条件结构。

(3)循环结构：在一些算法中，经常会出现从某处开始，按照一定条件，反复执行某一处理步骤的情况，这就是循环结构，反复执行的处理步骤为循环体，显然，循环结构中一定包含条件结构。 循环结构分为两类：

一类是当型循环结构，它的功能是当给定的条件P1成立时，执行A框，A框执行完毕后，再判断条件P1是否成立，如果仍然成立，再执行A框，如此反复执行A框，直到某一次条件P1不成立为止，此时不再执行A框，从b离开循环结构。

另一类是直到型循环结构，它的功能是先执行，然后判断给定的条件P2是否成立，如果P2仍然不成立，则继续执行A框，直到某一次给定的条件P2成立为止，此时不再执行A框，从b点离开循环结构。

两种循环结构有什么差别？

当型：先判断 后执行 先判断指定的条件是否为真，若条件为真，执行循环条件，条件为假时退出循环。

直到型：先执行 后判断 先执行循环体，然后再检查条件是否成立，如果不成立就重复执行循环体，直到条件成立退出循环。

注意：

1.对于算法的理解不能仅局限于解决数学问题的方法，解决任何问题的方法和步骤都应该是算法。算法具有概括性、抽象性、正确性等特点，要通过具体问题的过程和步骤的分析去体会算法的思想，了解算法的含义。

2.在学习程序框图时要掌握各程序框的作用，准确应用三种基本逻辑结构，即顺序结构、条件分支结构、循环结构来画程序框图准确表达算法。画程序框图是用基本语句来编程的前提。

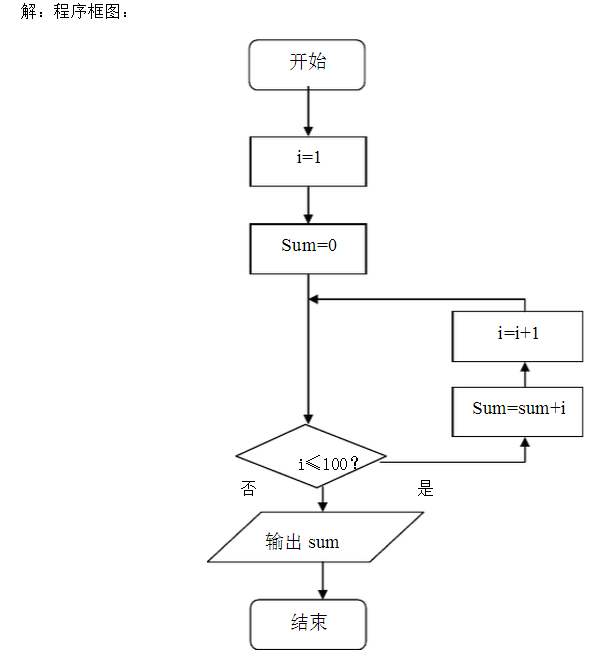
例3：设计一个计算1+2+„+100的值的算法，并画出程序框图。 算法分析：只需要一个累加变量和一个计数变量，将累加变量的初始值为0，计数变量的值可以从1到100。

例题

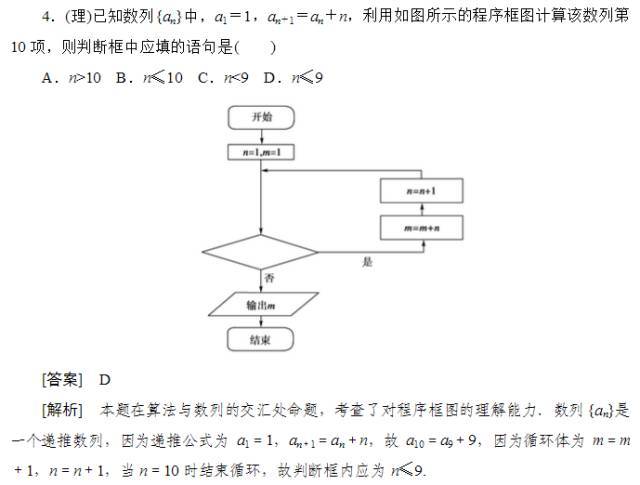
2．(理)下列程序运行后输出结果为( )

S＝1；

n＝1；

while S<100

S＝S*n；

n＝n＋3；

end

n =？

A．4

B．10

C．13

D．16

答案： C

解析： S＝1<100，进行第一次循环后S＝1，n＝4；S＝1<100再进行第二次循环。循环后S＝4，n＝7；第三次循环后S＝28，n＝10；第四次循环后S＝280，n＝13。因S＝280>100，故不再循环，跳出循环后输出n＝13。

---------------------------------------

------------------------------------------返回搜狐，查看更多

责任编辑：