全世界只有3.14 % 的人关注了
青少年数学之旅
何谓数学？
数学家Eduardo曾这样回答
“数学是永恒，是真理，是一切的答案。”
而这一切的发现，都离不开漫长数学史中的那一群人。
他们是科学文明的先驱者，引领数学浪潮，勇攀科技之巅；用字符谱写最动听的数学之歌，传唱于人类的历史长河上。
今天，超模君就来讲几个数学界大咖级别的常数。
毕达哥拉斯常数
没错，就是那个引发第一次数学危机的数字——√2 ≈ 1.4142135623730950488。
公元前500年，有一位牛人，叫毕达哥拉斯。如果你对这位牛人有点儿陌生，那毕达哥拉斯定理应该知道吧，那就是：直角三角形中，两直角边的平方和等于斜边的平方。
在中国，这被称为“勾股定理”。
他创办了一个数学学派，叫做毕达哥拉斯学派，该学派认为：整数就像原子一样，构成了宇宙中的一切，并可以描述宇宙中的一切。宇宙间各种关系都可以用整数或整数之比来表达，除此之外，就什么都没有了。。。
希勃索斯，在研究老师的定理时，发现了一个神奇的现象：边长为1的正方形，其对角线的长竟然无法用整数或整数之比表示出来！
于是，他把这个惊人的发现告诉了老师毕达哥拉斯。。。
希勃索斯本来以为老师会将这一发现公布于众，改变人们错误的认识。
没想到，老师却认为这样会动摇到毕达哥拉斯学派在学术界的统治地位，便新规定了一条纪律：谁都不准泄露存在根号2（即无理数）的秘密。
后来，天真的希勃索斯有一次无意中向别人谈到了他的发现，结果他被认为是学派的“逆贼”，被囚禁，受尽百般折磨，最后被投入爱琴海淹死。。。
关于希勃索斯的死有很多个版本，众说纷纭，但无论如何，希勃索斯都被人们当作是发现无理数的第一人。
√2就是第一个被发现的无理数，它的应用非常广泛，比如我们平常用的A4纸长宽之比就等于√2。
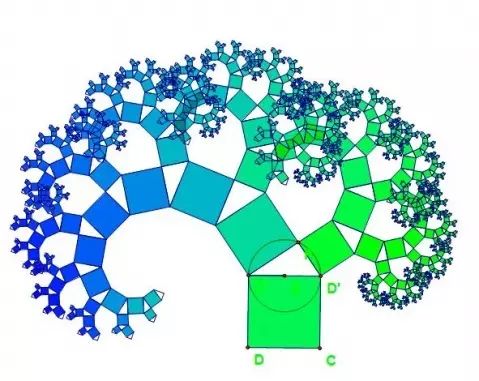
毕达哥拉斯树
辛钦常数
对于任意实数x，都可以写成下面的形式：
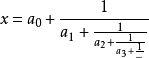
其中，a0,a1,a2……都是整数，而 [a0; a1, a2, a3, …] 就称为实数x的连分数展开。
苏联数学家辛钦Khinchin
1964年，数学家辛钦证明了一个惊人的结论：对于几乎所有实数x（除了有理数、实系数二次方程的解，以及自然对数的底e等特殊情况之外），其连分数表示式的系数ai的几何平均数会收敛到一个相同的数，且与实数x的数值无关。
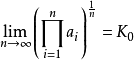
这个数就是辛钦常数，用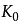
表示。
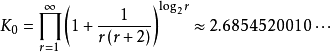
不过，对于这个神秘的常数，人们了解的还是很少，除了它的精确值不容易求出之外，关于辛钦常数是否为无理数，到目前也还没有人能证明。
圆周率π
圆周率 π ≈ 3.14159是圆的周长与直径的比值，是精确计算圆周长、圆面积、球体积等几何形状的关键值，人类很早就认识到了圆周率的存在。
公元前3世纪初，欧几里得在其著作《几何原本》中就提到过圆周率是常数；
公元前2世纪左右，中国古算书《周髀算经》中有“径一而周三”的记载，也认为圆周率是常数。
而如今用来表示圆周率的希腊字母π，本来与圆周率毫无关系，只是从1736年开始，欧拉在书信和论文中都用π来表示圆周率，久而久之，人们就普遍认同π就是圆周率了。
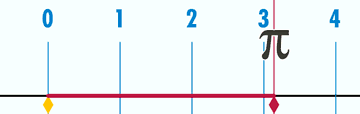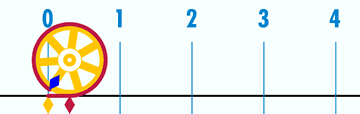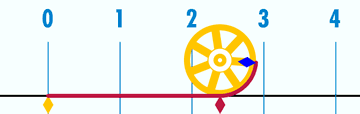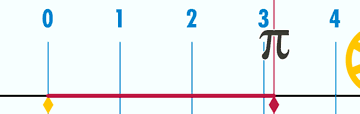
π应该是数学中最基本、最重要、最神奇的常数了，人类对它的探索就从来没停止过，不过，从它的出现到确定它是无理数，人类就花了3000年的时间。。。
直到1761年，德国数学家朗伯（Lambert）才证明了 π 是一个无理数。
1882 年，德国数学家林德曼（Ferdinand von Lindemann）证明了圆周率 π 是一个超越数。（不满足任一个整系数代数方程的数）
自然底数e
17世纪末，伯努利（Bernoulli）发现了一个有趣的现象，
会随着x的增大而越来越接近某个固定的数。
半个世纪后，欧拉才仔细研究了这个问题，并用字母 e 来表示这个常数：
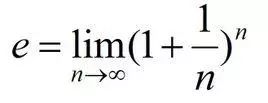
他不仅求出了e ≈ 2.718，还证明了 e 是一个无理数。
跟π一样， e 也是一个超越数，于1873 年被法国数学家夏尔·埃尔米特（Charles Hermite）证明。
复常数
数学中，还有一个很特别的常数，就是虚数单位 i ，它是指 -1 的开平方，它的出现，瞬间将整个数域又扩充了一半。
而最美公式——“欧拉恒等式”就将世界上最基本的两个数字 0，1，以及数学中最重要最基本的三大常数π、e、i 都联系到了一起，干净利落，简直漂亮到了神圣的地步！
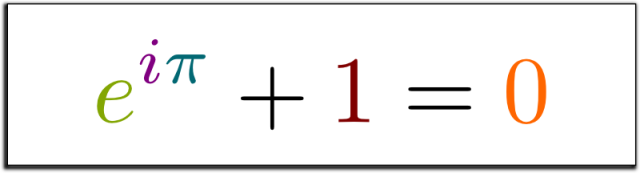
写在最后
无论是毕达哥拉斯常数、辛钦常数、复常数，还是圆周率π、自然底数e ，每一个数学常数都是开启数学之门的钥匙，都是这些顶尖数学家深邃的宝藏。
而我们推出的年度数学艺术礼盒《数学之旅 · 闪耀人类的54个数学家》，透过这一张张扑克牌，我们看到了一群迸发着智慧光芒的顶尖数学家，他们让我们更直观地明白什么才是数学之美！
正因如此，科学与数学的美在这里相聚，才拥有了惊叹千年的艺术魅力。
原价199
众筹价129
点击图片立即参与众筹
