题目描述:给定一个数组A[0,1,...,n-1],请构建一个数组B[0,1,...,n-1]。
其中B中的元素B[i]=A[0] * A[1]... * A[i-1] * A[i+1]... * A[n-1]。不能使用除法。
解题思路:首先,仔细理解题意,B[i]是A数组所有元素的乘积,但是没有A[i]项,如果没有不能使用除法这一限制,我们可以直接将A数组的所有元素相乘,得到一个乘积,记为res,则使用公式B[i] = res/A[i]即可得到B这个乘积数组。
现在有不能使用除法的限制,只能使用其他办法,当然,一个最直观的办法是每次计算B[i]时,都计算A数组中n-1个数字的乘积,显然这需要O(n^2)的时间复杂度。
仔细分析可以发现,这种暴力解法有很多重复的计算,我们可以通过一个简单的改变来避免这些重复计算。具体如下:
我们可以把B[i]=A[0]*A[1]*A[2]*···*A[i-1]*A[i+1]*···*A[n-1]看成是两部分的乘积,第一部分是i之前的所有项,记为C[i],即C[i]=A[0]*A[1]*A[2]*···*A[i-1],第二部分是i之后的所有项,记为D[i],即D[i]=A[i+1]*···*A[n-1]。经过这样的分隔后,数组B就相当于可以用如下的矩阵来构建,B[i]为矩阵中第i行所有元素的乘积。
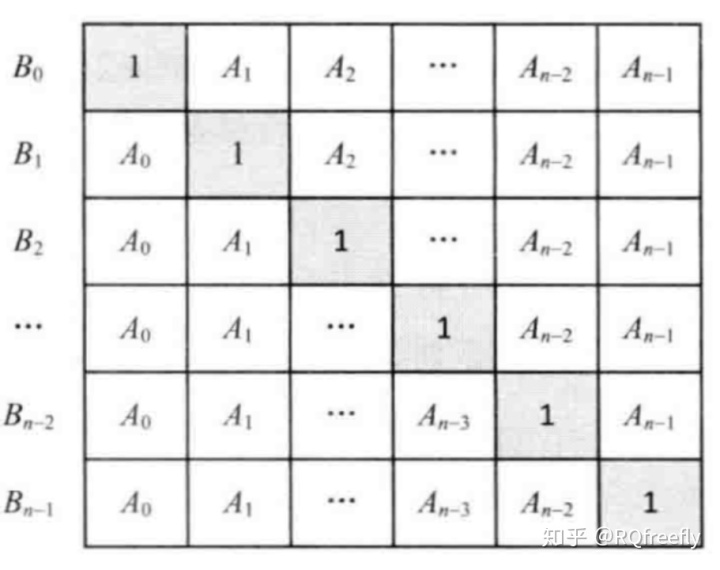
由此,我们不难得出相应的规律:首先B[i]=C[i]*D[i],而C[i]可以通过自上而下的顺序进行计算,即C[0]=1,C[i]=C[i-1]*A[i-1],同理,D[i]可以通过自下而上的顺序进行计算,即D[len-1]=1,D[i]=D[i+1]*A[i+1]。
代码如下所示,第一个for循环从上而下相当于计算C[i],第二个for循环自下而上相当于在C[i]的基础上乘以D[i]。显然时间复杂度为O(n)。
public int[] multiply(int[] A) {/*思路:分成两部分的乘积,第一部分可以自上而下,第二部分自下而上*/if(A==null||A.length<1)return A;int len=A.length;int[] B=new int[len]; B[0]=1;for(int i=1;i<len;i++) //第一部分可以自上而下B[i]=B[i-1]*A[i-1]; //如何要达到上图排序的效果就需要有这样的通项公式int temp=1; //temp用来保存第二部分for(int i=len-2;i>=0;i--){ //第二部分可以自下而上temp=temp*A[i+1];B[i]=B[i]*temp;}return B;
}




)


)


)







