转自：http://blog.csdn.net/dznlong/article/details/2261150
理解离散傅立叶变换（一）
------傅立叶变换的由来
关于傅立叶变换，无论是书本还是在网上可以很容易找到关于傅立叶变换的描述，但是大都是些故弄玄虚的文章，太过抽象，尽是一些让人看了就望而生畏的公式的罗列，让人很难能够从感性上得到理解，最近，我偶尔从网上看到一个关于数字信号处理的电子书籍，是一个叫Steven W. Smith, Ph.D.外国人写的，写得非常浅显，里面有七章由浅入深地专门讲述关于离散信号的傅立叶变换，虽然是英文文档，我还是硬着头皮看完了有关傅立叶变换的有关内容，看了有茅塞顿开的感觉，在此把我从中得到的理解拿出来跟大家分享，希望很多被傅立叶变换迷惑的朋友能够得到一点启发，这电子书籍是免费的，有兴趣的朋友也可以从网上下载下来看一下，URL地址是：
http://www.dspguide.com/pdfbook.htm
要理解傅立叶变换，确实需要一定的耐心，别一下子想着傅立叶变换是怎么变换的，当然，也需要一定的高等数学基础，最基本的是级数变换，其中傅立叶级数变换是傅立叶变换的基础公式。
一、傅立叶变换的提出
让我们先看看为什么会有傅立叶变换？傅立叶是一位法国数学家和物理学家的名字，英语原名是Jean Baptiste Joseph Fourier(1768-1830), Fourier对热传递很感兴趣，于1807年在法国科学学会上发表了一篇论文，论文里描述运用正弦曲线来描述温度分布，论文里有个在当时具有争议性的决断：任何连续周期信号都可以由一组适当的正弦曲线组合而成。当时审查这个论文的人，其中有两位是历史上著名的数学家拉格朗日(Joseph Louis Lagrange, 1736-1813)和拉普拉斯(Pierre Simon de Laplace, 1749-1827)，当拉普拉斯和其它审查者投票通过并要发表这个论文时，拉格朗日坚决反对，在近50年的时间里，拉格朗日坚持认为傅立叶的方法无法表示带有棱角的信号，如在方波中出现非连续变化斜率。法国科学学会屈服于拉格朗日的威望，否定了傅立叶的工作成果，幸运的是，傅立叶还有其它事情可忙，他参加了政治运动，随拿破仑远征埃及，法国大革命后因怕会被推上断头台而一直在逃避。直到拉格朗日死后15年这个论文才被发表出来。
谁是对的呢？拉格朗日是对的：正弦曲线无法组合成一个带有棱角的信号。但是，我们可以用正弦曲线来非常逼近地表示它，逼近到两种表示方法不存在能量差别，基于此，傅立叶是对的。
为什么我们要用正弦曲线来代替原来的曲线呢？如我们也还可以用方波或三角波来代替呀，分解信号的方法是无穷多的，但分解信号的目的是为了更加简单地处理原来的信号。用正余弦来表示原信号会更加简单，因为正余弦拥有原信号所不具有的性质：正弦曲线保真度。一个正余弦曲线信号输入后，输出的仍是正余弦曲线，只有幅度和相位可能发生变化，但是频率和波的形状仍是一样的。且只有正余弦曲线才拥有这样的性质，正因如此我们才不用方波或三角波来表示。
二、傅立叶变换分类
根据原信号的不同类型，我们可以把傅立叶变换分为四种类别：
| 1 | 非周期性连续信号 | 傅立叶变换（Fourier Transform） |
| 2 | 周期性连续信号 | 傅立叶级数(Fourier Series) |
| 3 | 非周期性离散信号 | 离散时域傅立叶变换（Discrete Time Fourier Transform） |
| 4 | 周期性离散信号 | 离散傅立叶变换(Discrete Fourier Transform) |
下图是四种原信号图例：
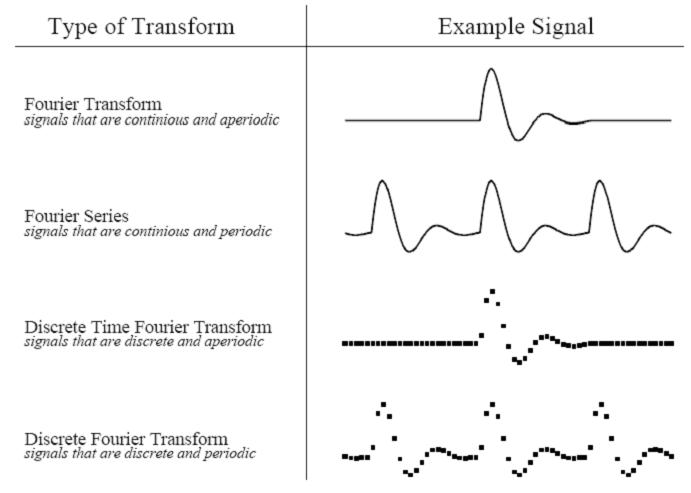
这四种傅立叶变换都是针对正无穷大和负无穷大的信号，即信号的的长度是无穷大的，我们知道这对于计算机处理来说是不可能的，那么有没有针对长度有限的傅立叶变换呢？没有。因为正余弦波被定义成从负无穷小到正无穷大，我们无法把一个长度无限的信号组合成长度有限的信号。面对这种困难，方法是把长度有限的信号表示成长度无限的信号，可以把信号无限地从左右进行延伸，延伸的部分用零来表示，这样，这个信号就可以被看成是非周期性离解信号，我们就可以用到离散时域傅立叶变换的方法。还有，也可以把信号用复制的方法进行延伸，这样信号就变成了周期性离解信号，这时我们就可以用离散傅立叶变换方法进行变换。这里我们要学的是离散信号，对于连续信号我们不作讨论，因为计算机只能处理离散的数值信号，我们的最终目的是运用计算机来处理信号的。
但是对于非周期性的信号，我们需要用无穷多不同频率的正弦曲线来表示，这对于计算机来说是不可能实现的。所以对于离散信号的变换只有离散傅立叶变换（DFT）才能被适用，对于计算机来说只有离散的和有限长度的数据才能被处理，对于其它的变换类型只有在数学演算中才能用到，在计算机面前我们只能用DFT方法，后面我们要理解的也正是DFT方法。这里要理解的是我们使用周期性的信号目的是为了能够用数学方法来解决问题，至于考虑周期性信号是从哪里得到或怎样得到是无意义的。
每种傅立叶变换都分成实数和复数两种方法，对于实数方法是最好理解的，但是复数方法就相对复杂许多了，需要懂得有关复数的理论知识，不过，如果理解了实数离散傅立叶变换(real DFT)，再去理解复数傅立叶变换就更容易了，所以我们先把复数的傅立叶变换放到一边去，先来理解实数傅立叶变换，在后面我们会先讲讲关于复数的基本理论，然后在理解了实数傅立叶变换的基础上再来理解复数傅立叶变换。
还有，这里我们所要说的变换(transform)虽然是数学意义上的变换，但跟函数变换是不同的，函数变换是符合一一映射准则的，对于离散数字信号处理（DSP），有许多的变换：傅立叶变换、拉普拉斯变换、Z变换、希尔伯特变换、离散余弦变换等，这些都扩展了函数变换的定义，允许输入和输出有多种的值，简单地说变换就是把一堆的数据变成另一堆的数据的方法。
三、一个关于实数离散傅立叶变换(Real DFT)的例子
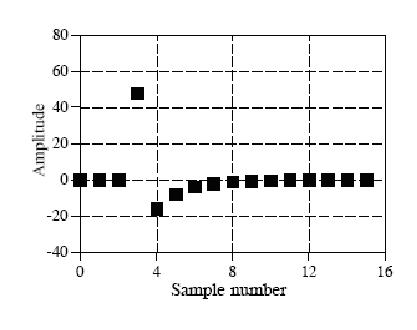
先来看一个变换实例，下图是一个原始信号图像：
这个信号的长度是16，于是可以把这个信号分解9个余弦波和9个正弦波（一个长度为N的信号可以分解成N/2+1个正余弦信号，这是为什么呢？结合下面的18个正余弦图,我想从计算机处理精度上就不难理解，一个长度为N的信号，最多只能有N/2+1个不同频率，再多的频率就超过了计算机所能所处理的精度范围），如下图：
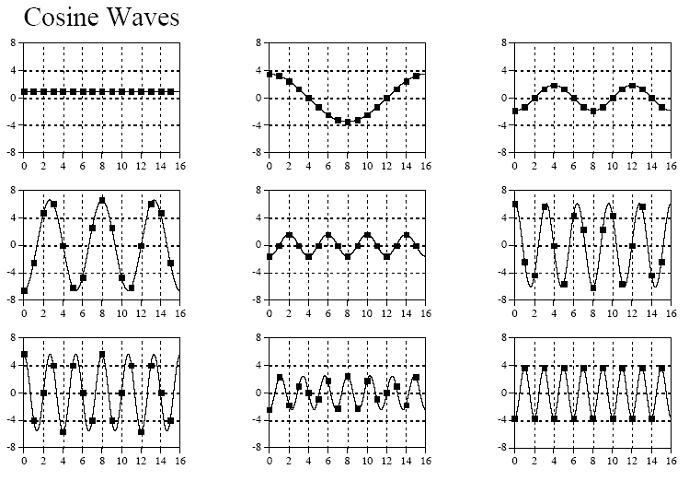
9个余弦信号：
9个正弦信号：
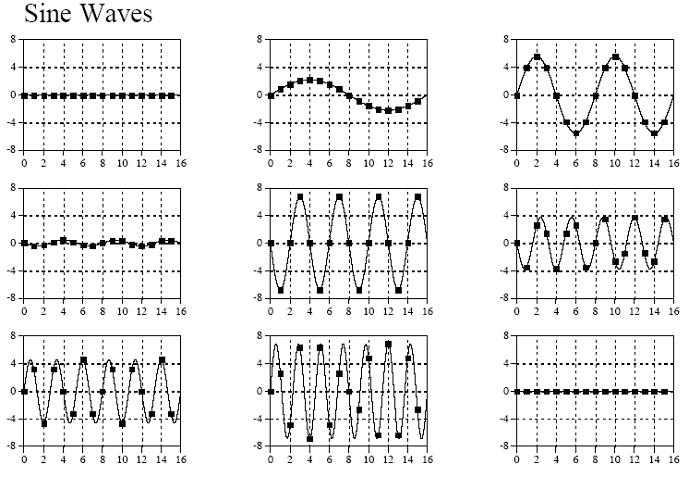
把以上所有信号相加即可得到原始信号，至于是怎么分别变换出9种不同频率信号的，我们先不急，先看看对于以上的变换结果，在程序中又是该怎么表示的，我们可以看看下面这个示例图：
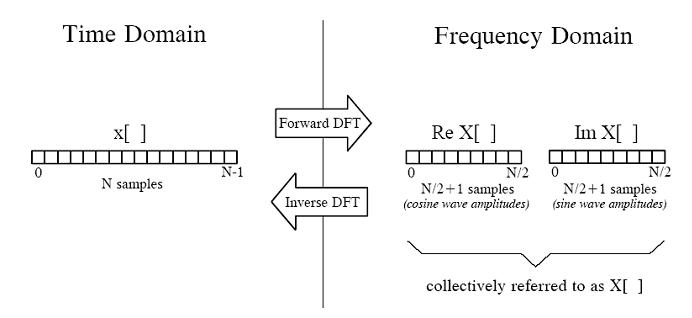
上图中左边表示时域中的信号，右边是频域信号表示方法，从左向右表示正向转换(Forward DFT)，从右向左表示逆向转换(Inverse DFT)，用小写x[]表示信号在每个时间点上的幅度值数组, 用大写X[]表示每种频率的副度值数组, 因为有N/2+1种频率，所以该数组长度为N/2+1，X[]数组又分两种，一种是表示余弦波的不同频率幅度值：Re X[]，另一种是表示正弦波的不同频率幅度值：Im X[]，Re是实数(Real)的意思，Im是虚数(Imagine)的意思，采用复数的表示方法把正余弦波组合起来进行表示，但这里我们不考虑复数的其它作用，只记住是一种组合方法而已，目的是为了便于表达（在后面我们会知道，复数形式的傅立叶变换长度是N，而不是N/2+1）。
下一节我们将来看一下实数傅立叶变换的具体方法。
