

源宝导读:在前端的开发中我们经常会遇到利用贝塞尔曲线帮助我们完成前端的动画和图形绘制,但是对其中的一些参数配置是一头雾水。本文将从贝塞尔曲线的原理讲起,由浅入深剖析一阶到多阶贝塞尔的实现原理,最后从三个方向来介绍它的实际应用。
一、IOS图标莫名的舒适感
先来对比下面两张图:

如果你用过苹果手机就都会有一种感觉,很多安卓手机的图标都会像左侧图标这样——倒角和直线的过渡处有些许不自然;而现在流行的IOS系统图标都是右侧的这种,圆润的倒角,这种就是有一种说不出来哪里来的舒适感:苹果的图标为什么看起来就是比一般的安卓图标要高级?
在IOS6以及以前的版本上,苹果都是用的倒圆角这种图标;但是2013年6月苹果在IOS7发布会上,苹果将iOS上标志性的圆角图标轮廓作了更新,将工业设计中的曲线连续概念应用到了视觉设计之上,而这个曲率连续的线,就是我们今天要提到的——贝塞尔曲线。
二、历史起源
贝塞尔曲线(Bézier curve),又称贝兹曲线或贝济埃曲线,是应用于二维图形应用程序的数学曲线。贝塞尔曲线于1962年由法国工程师皮埃尔·贝塞尔(Pierre Bézier)所广泛发表,他运用贝塞尔曲线来为汽车的主体进行设计。现在主流的曲线设计基本都会用到这条曲线;常用的矢量图形软件都会通过它来精确画出曲线,比如ps的钢笔工具等。
三、数学原理
这条线到底神器在哪?在日常开发中,我们常用的是二次贝塞尔曲线和三次贝塞尔曲线,二次贝塞尔曲线只需要用到三个点,即可绘制出一条的平滑曲率过度自然的曲线;而苹果手机的边框和图标的倒角设计则用到了四个点,就完成了近乎完美的曲线倒角,接下来我们将深入的了解原理看看这条线是如何实现的。
1)向量:
在了解贝塞尔曲线之前,需要先了解一个定义向量:
向量指具有大小和方向的量,它可以形象化地表示为带箭头的线段,二维里面向量是一个[x,y] ,三维则是[x,y,z];
重要的事情说三次!下面定义里所有介绍的P0P1...Pn,ABC..都是向量!都是向量!都是向量!(目前只讨论二维)
2)一阶贝塞尔曲线和多阶贝塞尔曲线:
下图是一到四阶的贝塞尔曲线的示意图
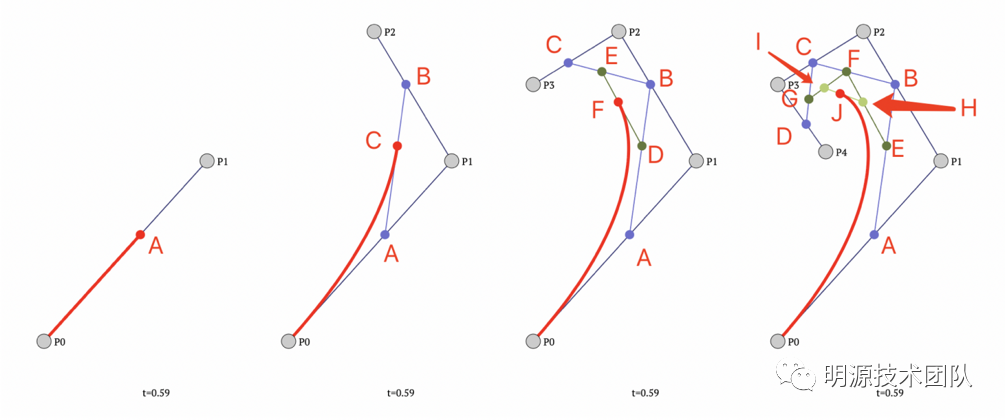
① 一阶:
其实很简单,看上图第一个图形,点A 随着时间t 在P0到P1上运动,所有点的集合就是一次贝塞尔曲线。
用向量的角度来看:
一次贝塞尔曲线 B(t),P0P1线段上随着时间t的变化( 0≤ t ≤1 ), P0表示向量 [x0 ,y0] P1表示向量 [x1, y1], A的值B(t)即为公式:
A = P0 + (P1-P0)*t
A = (1-t)P0 + t*P1
B(t) = (1-t)P0 + t*P1
结论:一阶贝塞尔曲线实际就是一条线段。
② 二阶:
他的定义是这样的:
由P0至P1的连续点A,描述一条线段;由P1至P2的连续点B,描述一条线段;由A至B的连续点C:B(t) 描述一条二次贝塞尔曲线。
那么这些点肯定遵守下面的规则,
t = (A - P0) / (P1 - P0) = ( B- P1) / (P2 - P1) = ( C - A ) / (B - A)
最终的公式如下:
A = (1-t)P0 + t*P1
B = (1-t)P1 + t*P2
C = (1-t)A + t*B
C = (1-t)( (1-t)P0 + t*P1 ) + t * ( (1-t)P1 + t*P2 )
C = (1-t)²P0 + 2t(1-t)P1 + t²P2;0≤t≤1
B(t) = (1-t)²P0 + 2t(1-t)P1 + t²P2;0≤t≤1
结论:二阶的贝塞尔通过在控制点之间再采点的方式实现降阶, 每一次选点都是一次的降阶。
③ 三阶:
理解了二阶以后,三阶可以依葫芦画瓢很快得出
A = (1-t)P0 + t*P1
B = (1-t)P1 + t*P2
C = (1-t)P2 + t*P3
D = (1-t)A + t*B
E = (1-t)B + t*C
F = (1-t)D + t*E
F = ....
结论:这个不就是递归嘛?
总结:
两个点对应一阶的贝塞尔曲线,三个点对应二阶,四个点对应三阶;
每一次的计算都一个降阶计算,高阶的贝塞尔可以通过不停的递归直到一阶。
n个控制点对应着n-1阶的贝塞尔曲线,并且可以通过递归的方式来绘制。
3)公式
通用公式:
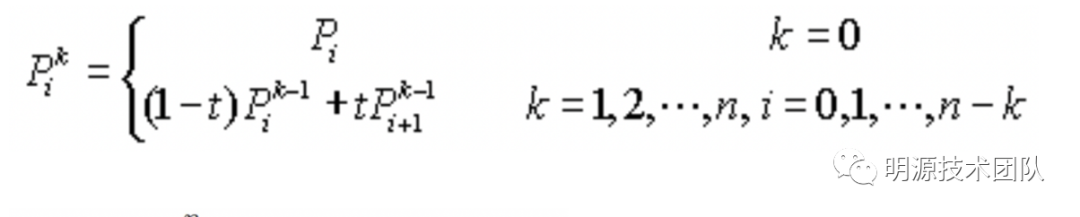
或者导数表示:
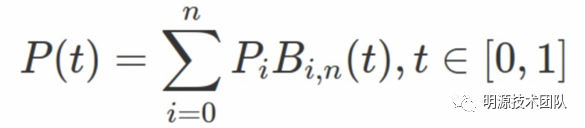
感兴趣的同学可以下去研究一下,这里就不做过于深入的研究了。
四、贝塞尔曲线在前端的应用
贝塞尔曲线在web前端主要在三处会用到:分别是css,svg,canvas
1) svg
svg的path路径d属性,支持二次(二阶)贝塞尔曲线和三次(三阶)贝塞尔曲线,缩写:
C和Q,例如:
Q 300 300, 500 100 二阶
C 200 200, 400 200, 500 100 三阶
我们先来看看一个demo,如下图的曲线:
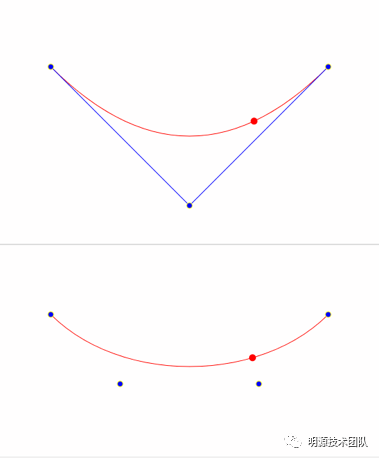
要实现上图的效果,看下图第二行代码svg的path属性当中 d的值:
M100 100 Q 300 300, 500 100 实际就是对应的二次贝塞尔曲线的,三个点:
第一个点:Q 前面的 100 100 起始点对应P0,
第二个点:Q后面第一个点 300 300 对应控制点P1
第三个点:Q后面的第二个点 500 100 对应结束点 P2
依此类推:类ball02:
M100 100 C 200 200, 400 200, 500 100 就是对应的三次贝塞尔曲线的,四个点:
第一个点:C 前面的M 100 100 起始点对应P0
第二个点:C后面第一个点 200 200 对应控制点P1
第三个点:C后面第二个点 400 200 对应结束点 P2
第四个点:C后面第三个点 500 100 对应结束点 P3
放代码:

补充小知识点:
下面的命令可用于路径path的d属性和offset-path的path属性:
M = moveto
L = lineto
H = horizontal lineto
V = vertical lineto
C = curveto
S = smooth curveto
Q = quadratic Belzier curve
T = smooth quadratic Belzier curveto
A = elliptical Arc
Z = closepath
属于贝塞尔曲的有:
C S Q T
2) css3
① offset-path路径
offset-path css的移动路径 可以用path的简写语法, 上面的svg的代码已写明
就是如下这种形式
offset-path: path('M100 100 Q 300 300, 500 100')
② cubic-bezier函数
函数 css3的cubic-bezier函数,主要就是在:
animation-timing-function(设置动画将如何完成一个周期)
transition-timing-function, 属性(设置动画过渡的效果)当中使用
含义 cubic-bezier(x1,y1,x2,y2)函数具体含义如下,如下对应贝塞尔曲线的P0,P1,P2,P3
P0:默认值 (0, 0)
P1:动态取值 (x1, y1)
P2:动态取值 (x2, y2)
P3:默认值 (1, 1)
技巧 在css3中我们常用的几个过渡效果其实都是用贝塞尔曲线的形式来表示的,这些方法名就叫缓动函数(文章末尾会附上缓动函数):
ease: cubic-bezier(0.25, 0.1, 0.25, 1.0)
linear: cubic-bezier(0.0, 0.0, 1.0, 1.0)
ease-in: cubic-bezier(0.42, 0, 1.0, 1.0)
ease-out: cubic-bezier(0, 0, 0.58, 1.0)
ease-in-out: cubic-bezier(0.42, 0, 0.58, 1.0)
注意的点 :
css3的贝塞尔曲线只有2阶和3阶的,并且将贝塞尔曲线做了一个限制:除了所有参数必需,参数是数字值以外;x1 和 x2 需要是 0 到 1 的数字。比较常见transitio的动画例如:宽度大小变化,颜色渐变,位置移动,内外边距等,animation的话可以结合@keyframe 实现一些关键帧动画,效果更好
Demo:

3) canvas
canvas比较简单,语法如下:
1. 二阶:quadraticCurveTo(x1,y1, x2,y2)
2. 三阶:bezierCurveTo(x1,y1, x2,y2, x3,y3)
上面的二阶,三阶 和 svg的 C,Q 是一样的语法,就不赘述了。
有一个波浪的效果这里全部是用canvas绘制的,代码贴在文章末尾。

具体代码:
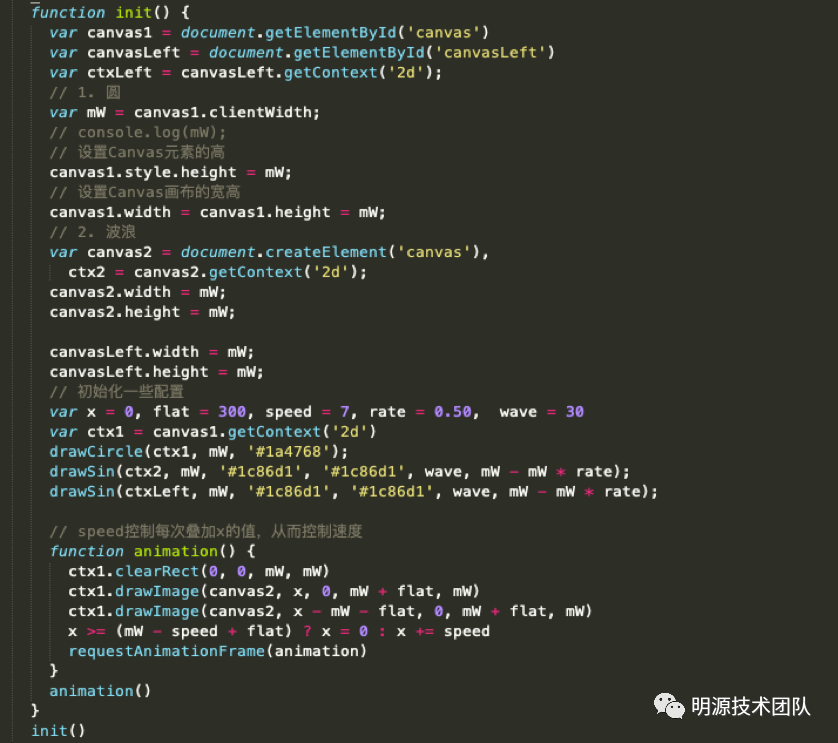
分三块:
1.dom区域:定义容器和尺寸,这个很好理解。

第二个区域:绘制外圈的圆形drawCircle和波浪效果 drawSin的方法。
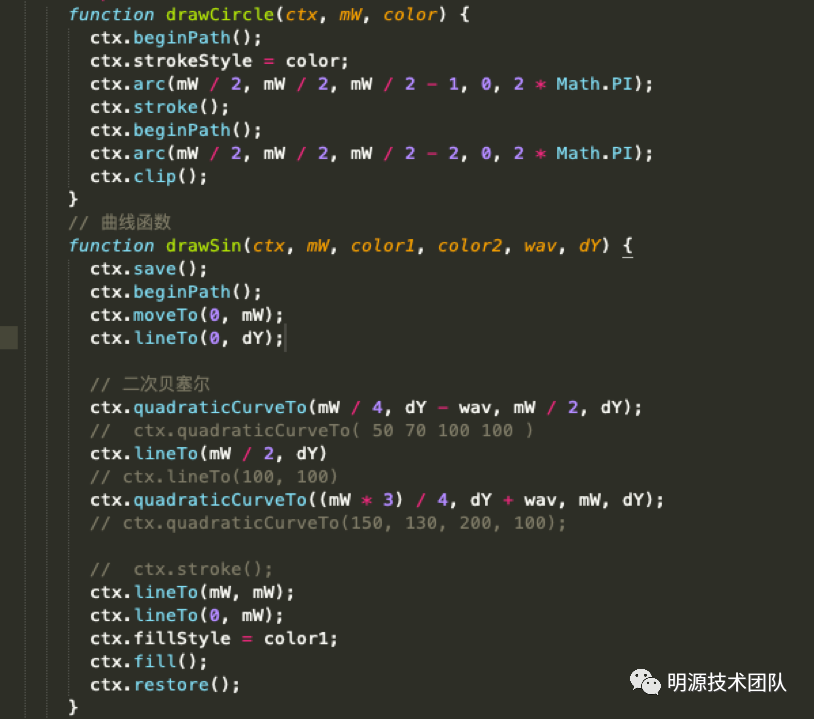
第三个区域:绘制动画,利用requestAnimationFrame方法不断的重新绘制波浪效果(animation方法),不停的重复累加X轴横向位置,这样就可以实现一个不断的波浪。
五、写在结尾的话
贝塞尔曲线这条神器的曲线在前端的应用还是相当广泛的,除了常见的css动画,过渡效果,在svg和canvas的动画当中也必不可少,掌握上述的三个方向,对面大部分的场景,前端的同学都能够游刃有余的去应付。
文章如有纰漏可以在评论里指正交流。
文中用到的代码:
链接: https://pan.baidu.com/s/1aMFK4Dehiz5KjddxN704vw 密码: b404
1. 曲线篇: 贝塞尔曲线 https://zhuanlan.zhihu.com/p/136647181
2. svg路径绘制 http://svg.wxeditor.com/
3. 缓动函数 https://www.xuanfengge.com/easeing/easeing/
另外附上css3 cubic-bezier函数 缓动效果集合:
$easeInSine: cubic-bezier(0.47, 0, 0.745, 0.715);
$easeOutSine: cubic-bezier(0.39, 0.575, 0.565, 1);
$easeInOutSine: cubic-bezier(0.445, 0.05, 0.55, 0.95);
$easeInQuad: cubic-bezier(0.55, 0.085, 0.68, 0.53);
$easeOutQuad: cubic-bezier(0.25, 0.46, 0.45, 0.94);
$easeInOutQuad: cubic-bezier(0.455, 0.03, 0.515, 0.955);
$easeInCubic: cubic-bezier(0.55, 0.055, 0.675, 0.19);
$easeOutCubic: cubic-bezier(0.215, 0.61, 0.355, 1);
$easeInOutCubic: cubic-bezier(0.645, 0.045, 0.355, 1);
$easeInQuart: cubic-bezier(0.895, 0.03, 0.685, 0.22);
$easeOutQuart: cubic-bezier(0.165, 0.84, 0.44, 1);
$easeInOutQuart: cubic-bezier(0.77, 0, 0.175, 1);
$easeInQuint: cubic-bezier(0.755, 0.05, 0.855, 0.06);
$easeOutQuint: cubic-bezier(0.23, 1, 0.32, 1);
$easeInOutQuint: cubic-bezier(0.86, 0, 0.07, 1);
$easeInExpo: cubic-bezier(0.95, 0.05, 0.795, 0.035);
$easeOutExpo: cubic-bezier(0.19, 1, 0.22, 1);
$easeInOutExpo: cubic-bezier(1, 0, 0, 1);
$easeInCirc: cubic-bezier(0.6, 0.04, 0.98, 0.335);
$easeOutCirc: cubic-bezier(0.075, 0.82, 0.165, 1);
$easeInOutCirc: cubic-bezier(0.785, 0.135, 0.15, 0.86);
$easeInBack: cubic-bezier(0.6, -0.28, 0.735, 0.045);
$easeOutBack: cubic-bezier(0.175, 0.885, 0.32, 1.275);
$easeInOutBack: cubic-bezier(0.68, -0.55, 0.265, 1.55);
------ END ------
作者简介
曹同学: 数据分析平台的开发工程师,目前负责天际平台相关开发工作。
也许您还想看:
技术分享|Java SDK动态数据源和上下文机制
技术分享|NodeJS分布式链路追踪实现
技术分享 | Java SDK 元数据驱动的事件通信架构
技术分享|Hangfire深度实践
技术分享 | APT结合JavaPoet生成模板化Java源代码文件
技术分享 | 玩转高效UI自动化测试
更多明源云·天际开放平台场景案例与开发小知识,可以关注明源云天际开发者社区公众号:
【建模】文档服务提供高保真打印模式
明源云·天际硬核技术认可:获华为鲲鹏技术认证书
天际·开发者社区“重装发布”!













)






