导读:算法哥好久没分享有趣的算法题了,有点寂寞空虚冷,今天看到一道似曾相识的题目,而且难度是hard模式,勾起了算法哥的征服欲。特分享之!
题目描述
「推箱子」是一款风靡全球的益智小游戏,玩家需要将箱子推到仓库中的目标位置。
游戏地图用大小为 m * n 的网格 grid 表示,其中每个元素可以是墙、地板或者是箱子。
现在你将作为玩家参与游戏,按规则将箱子 'B' 移动到目标位置 'T' :
玩家用字符 'S' 表示,只要他在地板上,就可以在网格中向上、下、左、右四个方向移动。
地板用字符 '.' 表示,意味着可以自由行走。
墙用字符 '#' 表示,意味着障碍物,不能通行。
箱子仅有一个,用字符 'B' 表示。相应地,网格上有一个目标位置 'T'。
玩家需要站在箱子旁边,然后沿着箱子的方向进行移动,此时箱子会被移动到相邻的地板单元格。记作一次「推动」。玩家无法越过箱子。返回将箱子推到目标位置的最小 推动 次数,如果无法做到,请返回 -1。
题目来源:LeetCode 1263

示例一
题目分析
其实这个题目,一看就能想到需要用广度优先搜索算法(BFS),我们也很自然的会想到,模拟推箱子的过程即可!
过程:
以箱子为起点,尝试每一步4个方向移动,移动的前提是,人可以达到箱子移动过去的格子的反方向的格子!所以这里还需要判断一下,人从当前位置是否可以到达那个反方向的格子。至此题目的思路就出来了。
在BFS的时候,我们需要把搜索过的人和箱子的位置做一个标记,防止重复搜索,因为变化位置的只有可能是人的位置,以及箱子的位置,所以我们可以用一个四维数组来标记人和箱子的状态,BFS过程中,检查一下人和箱子的位置是不是以前搜索过,搜索过就放弃,反之就继续搜索!
显然,搜索的起点是初始状态下箱子和人的位置,我们标记为(bx,by)和(sx,sy),初始移动次数是0,然后我们从起点出发,遍历箱子的4个方向,检查是否可以推过去(推过去的格子是不是墙,人是不是可以到达推过去格子反方向的格子),如果可以,把新的箱子位置和人的位置,以及推动箱子次数,作为一个新的状态加入到BFS的队列里,继续搜索直到走到位置T.
源码如下:
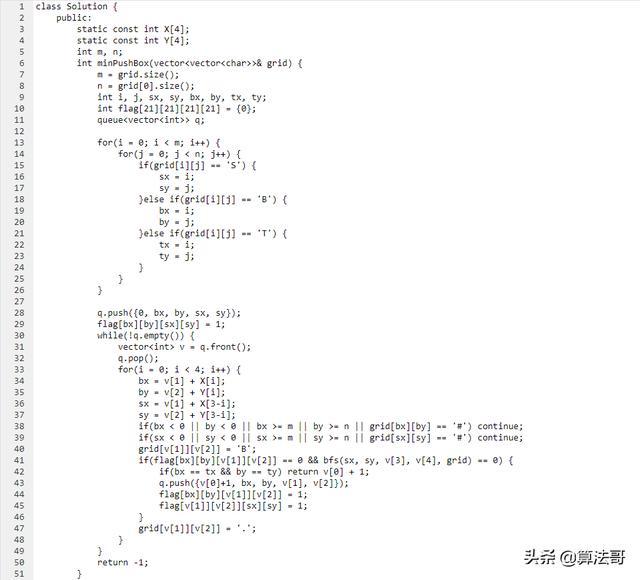
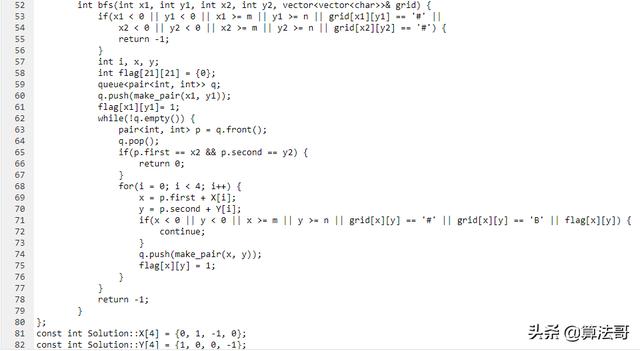
源码
复杂度分析
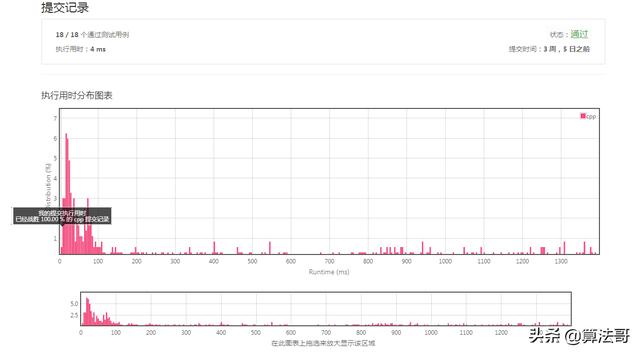
运行时间空间
复杂度,首先我们搜索的时候是从人和箱子的位置来搜索的,箱子的位置有m*n种,人的位置也有m*n种,但是实际在搜索过程中,人永远在箱子相邻4个格子,所以人的位置对于每个箱子位置是4个,总的搜索状态是m*n*4的,其次每次推动过程中有一次判断人的位置是否可以到达箱子推动方向反方向的格子的判断,这个步骤是m*n的复杂度,所以总的时间复杂度是O(m*n*m*n)的,击败了100%的提交!
总结
这个题目是一个比较经典的BFS算法的题目,虽然比较容易想到,但是实现起来是有一定难度的,主要要解决以下几个问题:
- 想到模拟箱子推动的过程,用BFS算法模拟;
- 知道根据箱子和人的位置来标记已经搜索过的状态;
- 两层BFS的嵌套使用,外层BFS解决箱子搜索的问题,里层BFS解决判断人是否可达到箱子推动反方向格子的问题;
- 一些编码上的技巧,比如通过方向向量,向4个方向搜索等;
题目分享完毕,记得给算法哥点赞、分享、评论、转发哦!这都是算法哥继续分享下去的最大鼓励!

备份当前的工作区的内容)



...)
)












