KMP算法配图详解
前言
KMP算法是我们数据结构串中最难也是最重要的算法。难是因为KMP算法的代码很优美简洁干练,但里面包含着非常深的思维。真正理解代码的人可以说对KMP算法的了解已经相当深入了。而且这个算法的不少东西的确不容易讲懂,很多正规的书本把概念一摆出直接劝退无数人。这篇文章将尽量以最详细的方式配图介绍KMP算法及其改进。文章的开始我先对KMP算法的三位创始人Knuth,Morris,Pratt致敬,懂得这个算法的流程后你真的不得不佩服他们的聪明才智。
KMP解决的问题类型
KMP算法的作用是在一个已知字符串中查找子串的位置,也叫做串的模式匹配。比如主串s=“goodgoogle”,子串t=“google”。现在我们要找到子串t 在主串s 中的位置。大家肯定觉得这还不简单,不就在第五个嘛,一眼就看出来了。
当然,在字符串非常少时,“肉眼观察法”不失为一个好方法。但如果要你在一千行文本里找一个单词,我想一般人都会数得崩溃吧。这就让我想起来考试的时候,如果一两道选择题不会。这时候,“肉眼观察法”可能效果不错,但是如果好几道大题不会呢?“肉眼观察法”就丝毫不起效了。所以打铁还需自身硬,我们把这种枯燥的事以一定的算法交给计算机处理。
第一种我们容易想到的就是暴力求解法。
这种方法也叫朴素的模式匹配:
简单来说就是:从主串s 和子串t 的第一个字符开始,将两字符串的字符一一比对,如果出现某个字符不匹配,主串回溯到第二个字符,子串回溯到第一个字符再进行一一比对。如果出现某个字符不匹配,主串回溯到第三个字符,子串回溯到第一个字符再进行一一比对…一直到子串字符全部匹配成功。
下面我们通过图片展示这个过程:
竖直线表示相等,闪电线表示不等
第一个过程:子串“goo”部分与主串相等,'g’不等,结束比对,进行回溯。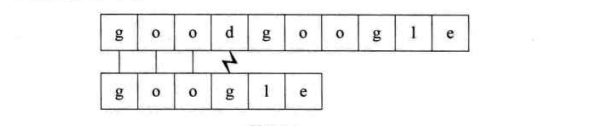
第二个过程:开始时就不匹配,直接回溯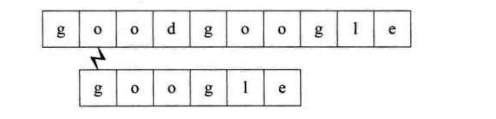
第三个过程:开始时即不匹配,直接回溯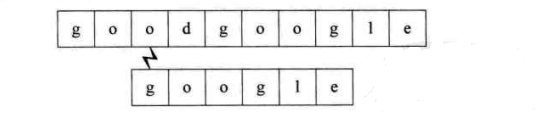
第四个过程:开始时即不匹配,直接回溯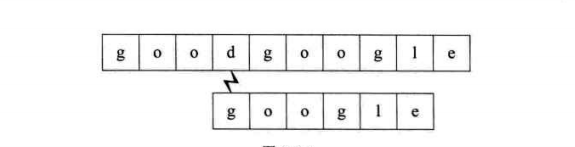
第五个过程:匹配成功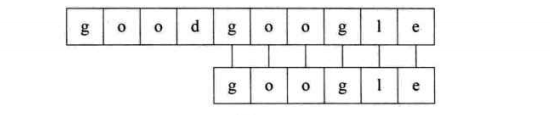
大家可能会想:这个方法也太慢了吧!求一个子串位置需要太多的步骤。而且很多步骤根本不必要进行。
这个想法非常好!!很多伟大的思想都是在一步步完善更正已有方法中诞生的。这种算法在最好情况下时间复杂度为O(n)。即子串的n个字符正好等于主串的前n个字符,而最坏的情况下时间复杂度为O(m*n)。相比而言这种算法空间复杂度为O(1),即不消耗空间而消耗时间。
下面就开始进入我们的正题:KMP算法是怎样优化这些步骤的。其实KMP的主要思想是:“空间换时间”。
大家打起精神,认真看下面的内容。
首先,为什么朴素的模式匹配这么慢呢?
你再回头看一遍就会发现,哦,原来是回溯的步骤太多了。所以我们应该尽量减少回溯的次数。
怎样做呢?比如上面第一个图:当字符’d’与’g’不匹配,我们保持主串的指向不变,
主串依然指向’d’,而把子串进行回溯,让’d’与子串中’g’之前的字符再进行比对。
如果字符匹配,则主串和子串字符同时右移。
至于子串回溯到哪个字符,这个问题我们先放一放。
我先提出一个概念:一个字符串最长相等前缀和后缀。
教科书常用的手段是:在此处摆出一堆数学公式让大家自行理解。
这也是为什么看计算机学科的书没有较好的数学基础会很痛苦。(当初我为什么不好好学数学T_T)
大家先不要强行理解数学公式,且听我慢慢道来:
我给大家个例子。
字符串 abcdab
前缀的集合:{a,ab,abc,abcd,abcda}
后缀的集合:{b,ab,dab,cdab,bcdab}
那么最长相等前后缀不就是ab嘛.
做个小练习吧:
字符串:abcabfabcab中最长相等前后缀是什么呢:
对就是abcab
好了我们现在会求一个字符串的前缀,后缀以及最长相等前后缀了。
这个概念很重要。到这里如果都看懂了,可以鼓励一下自己,然后回想一遍,再往下看。
之前留了一个问题,子串回溯到哪个字符,现在可以着手解决了。
图解KMP
现在我们先看一个图:第一个长条代表主串,第二个长条代表子串。红色部分代表两串中已匹配的部分,
绿色和蓝色部分分别代表主串和子串中不匹配的字符。
再具体一些:这个图代表主串"abcabeabcabcmn"和子串"abcabcmn"。
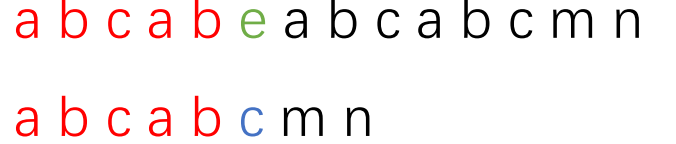
现在发现了不匹配的地方,根据KMP的思想我们要将子串向后移动,现在解决要移动多少的问题。
之前提到的最长相等前后缀的概念有用处了。因为红色部分也会有最长相等前后缀。如下图:
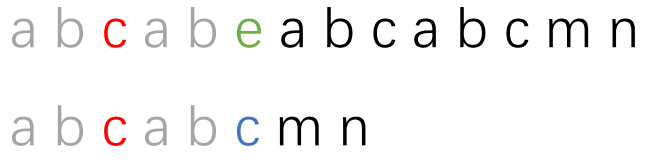
灰色部分就是红色部分字符串的最长相等前后缀,我们子串移动的结果就是让子串的红色部分最长相等前缀和主串红色部分最长相等后缀对齐。
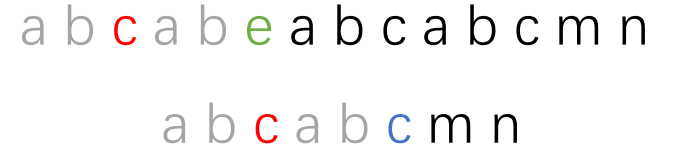
这一步弄懂了,KMP算法的精髓就差不多掌握了。接下来的流程就是一个循环过程了。事实上,每一个字符前的字符串都有最长相等前后缀,而且最长相等前后缀的长度是我们移位的关键,所以我们单独用一个next数组存储子串的最长相等前后缀的长度。而且next数组的数值只与子串本身有关。
所以next[i]=j,含义是:下标为i 的字符前的字符串最长相等前后缀的长度为j。
我们可以算出,子串t= "abcabcmn"的next数组为next[0]=-1(前面没有字符串单独处理)
next[1]=0;next[2]=0;next[3]=0;next[4]=1;next[5]=2;next[6]=3;next[7]=0;
| a | b | c | a | b | c | m | n |
|---|---|---|---|---|---|---|---|
| next[0] | next[1] | next[2] | next[3] | next[4] | next[5] | next[6] | next[7] |
| -1 | 0 | 0 | 0 | 1 | 2 | 3 | 0 |
本例中的蓝色c处出现了不匹配(是s[5]!=t[5]),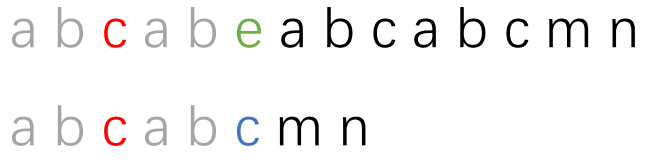
我们把子串移动,也就是让s[5]与t[5]前面字符串的最长相等前缀后一个字符再比较,而该字符的位置就是t[?],很明显这里的?是2,就是不匹配的字符前的字符串 最长相等前后缀的长度。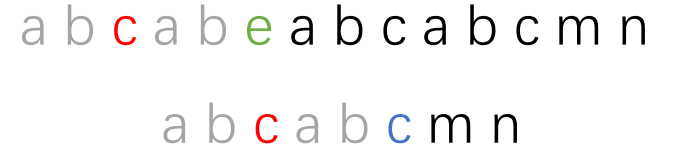
也是不匹配的字符处的next数组next[5]应该保存的值,也是子串回溯后应该对应的字符的下标。 所以?=next[5]=2。接下来就是比对是s[5]和t[next[5]]的字符。这里也是最奇妙的地方,也是为什么KMP算法的代码可以那么简洁优雅的关键。
我们可以总结一下,next数组作用有两个:
一是之前提到的,
next[i]的值表示下标为i的字符前的字符串最长相等前后缀的长度。
二是:
表示该处字符不匹配时应该回溯到的字符的下标
next有这两个作用的源头是:之前提到的字符串的最长相等前后缀
想一想是不是觉得这个算法好厉害,从而不得不由衷佩服KMP算法的创始人们。
KMP算法的时间复杂度
现在我们分析一下KMP算法的时间复杂度:
KMP算法中多了一个求数组的过程,多消耗了一点点空间。我们设主串s长度为n,子串t的长度为m。求next数组时时间复杂度为O(m),因后面匹配中主串不回溯,比较次数可记为n,所以KMP算法的总时间复杂度为O(m+n),空间复杂度记为O(m)。相比于朴素的模式匹配时间复杂度O(m*n),KMP算法提速是非常大的,这一点点空间消耗换得极高的时间提速是非常有意义的,这种思想也是很重要的。
下面还有更厉害的,我们一起来分析具体的代码。
求next数组的代码
下面我们一起来欣赏计算机如何求得next数组的
typedef struct
{ char data[MaxSize];int length; //串长
} SqString;
//SqString 是串的数据结构
//typedef重命名结构体变量,可以用SqString t定义一个结构体。
void GetNext(SqString t,int next[]) //由模式串t求出next值
{int j,k;j=0;k=-1;next[0]=-1;//第一个字符前无字符串,给值-1while (j<t.length-1) //因为next数组中j最大为t.length-1,而每一步next数组赋值都是在j++之后//所以最后一次经过while循环时j为t.length-2{ if (k==-1 || t.data[j]==t.data[k]) //k为-1或比较的字符相等时{ j++;k++;next[j]=k;//对应字符匹配情况下,s与t指向同步后移//通过字符串"aaaaab"求next数组过程想一下这一步的意义//printf("(1) j=%d,k=%d,next[%d]=%d\n",j,k,j,k);}else{k=next[k];**//我们现在知道next[k]的值代表的是下标为k的字符前面的字符串最长相等前后缀的长度//也表示该处字符不匹配时应该回溯到的字符的下标//这个值给k后又进行while循环判断,此时t.data[k]即指最长相等前缀后一个字符**//为什么要回退此处进行比较,我们往下接着看。其实原理和上面介绍的KMP原理差不多//printf("(2) k=%d\n",k);}}
}
解释next数组构造过程中的回溯问题
大家来看下面的图:
下面的长条代表子串,红色部分代表当前匹配上的最长相等前后缀,蓝色部分代表t.data[j]。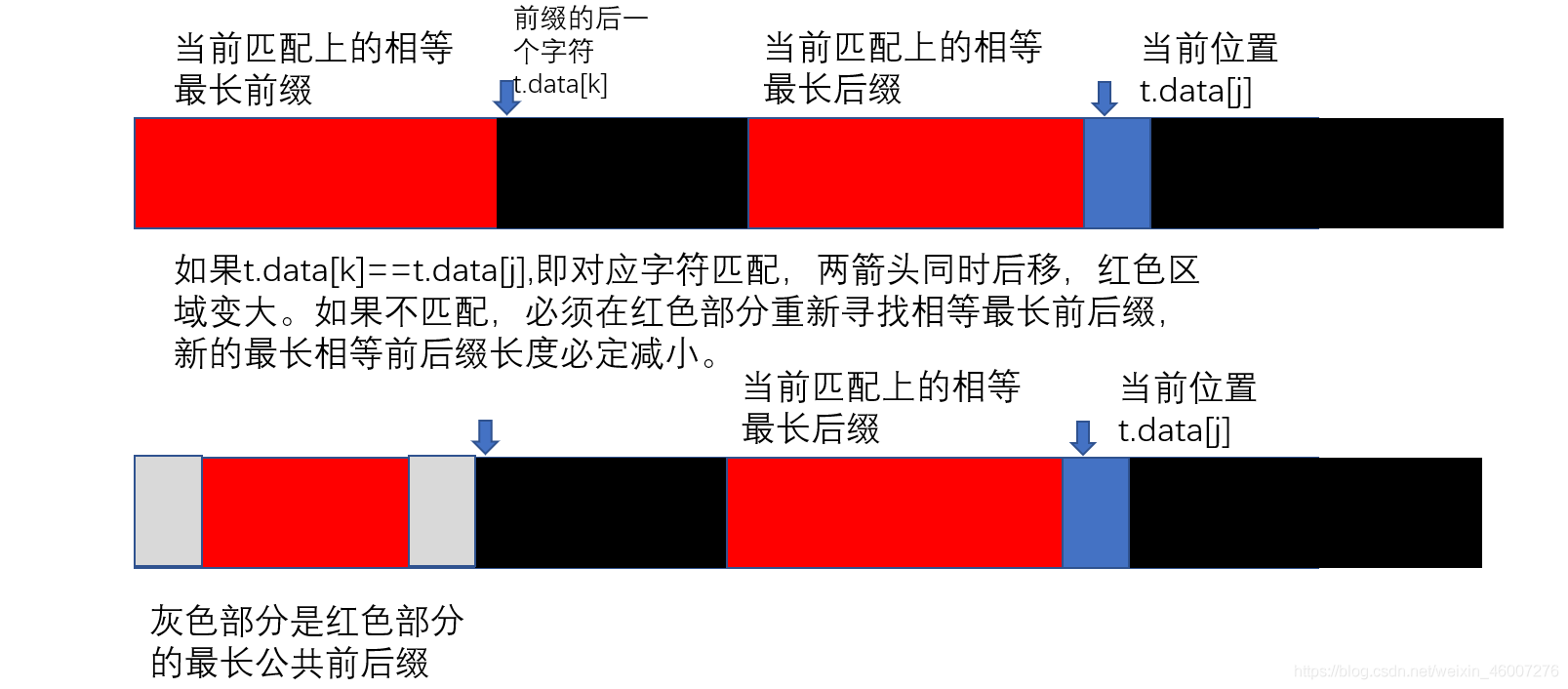
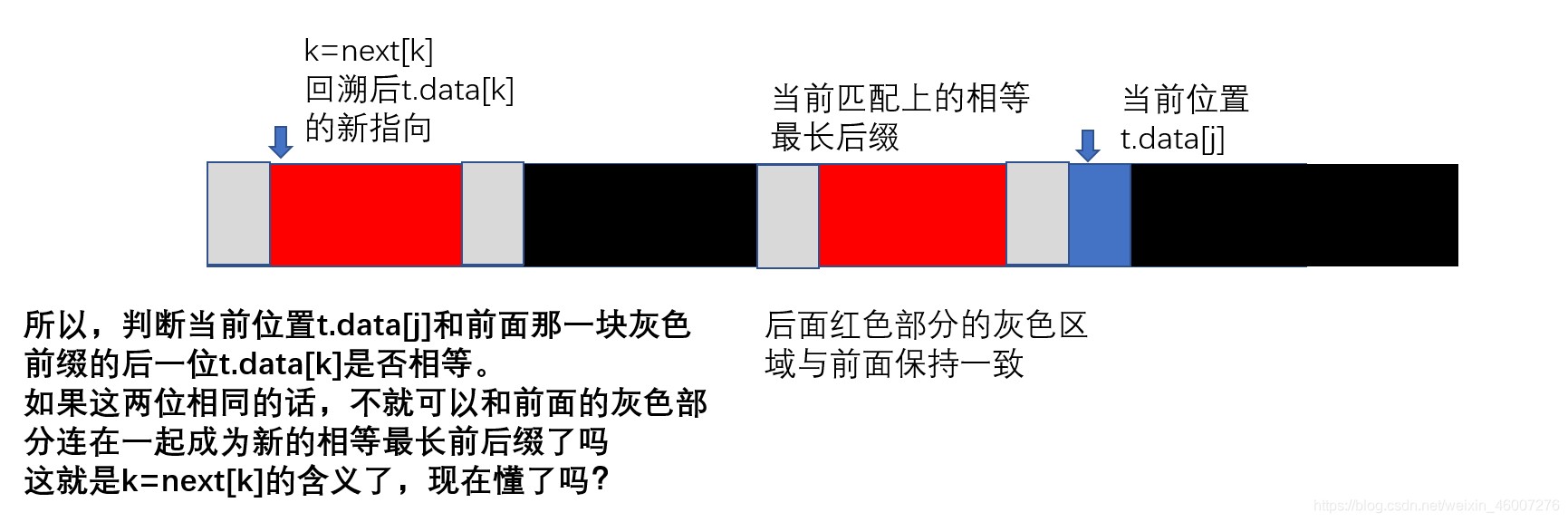
KMP算法代码解释
int KMPIndex(SqString s,SqString t) //KMP算法
{int next[MaxSize],i=0,j=0;GetNext(t,next);while (i<s.length && j<t.length) {if (j==-1 || s.data[i]==t.data[j]) {i++;j++; //i,j各增1}else j=next[j]; //i不变,j后退,现在知道为什么这样让子串回退了吧}if (j>=t.length)return(i-t.length); //返回匹配模式串的首字符下标else return(-1); //返回不匹配标志
}
KMP算法的改进
为什么KMP算法这么强大了还需要改进呢?
大家来看一个例子:
主串s=“aaaaabaaaaac”
子串t=“aaaaac”
这个例子中当‘b’与‘c’不匹配时应该‘b’与’c’前一位的‘a’比,这显然是不匹配的。'c’前的’a’回溯后的字符依然是‘a’。
我们知道没有必要再将‘b’与‘a’比对了,因为回溯后的字符和原字符是相同的,原字符不匹配,回溯后的字符自然不可能匹配。但是KMP算法中依然会将‘b’与回溯到的‘a’进行比对。这就是我们可以改进的地方了。我们改进后的next数组命名为:nextval数组。KMP算法的改进可以简述为: 如果a位字符与它next值指向的b位字符相等,则该a位的nextval就指向b位的nextval值,如果不等,则该a位的nextval值就是它自己a位的next值。 这应该是最浅显的解释了。如字符串"ababaaab"的next数组以及nextval数组分别为:
| 下标 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|---|
| 子串 | a | b | a | b | a | a | a | b |
| next | -1 | 0 | 0 | 1 | 2 | 3 | 1 | 1 |
| nextval | -1 | 0 | -1 | 0 | -1 | 3 | 1 | 0 |
我们来分析下代码:
void GetNextval(SqString t,int nextval[])
//由模式串t求出nextval值
{int j=0,k=-1;nextval[0]=-1;while (j<t.length) {if (k==-1 || t.data[j]==t.data[k]) { j++;k++;if (t.data[j]!=t.data[k])
//这里的t.data[k]是t.data[j]处字符不匹配而会回溯到的字符
//为什么?因为没有这处if判断的话,此处代码是next[j]=k;
//next[j]不就是t.data[j]不匹配时应该回溯到的字符位置嘛nextval[j]=k;else nextval[j]=nextval[k];
//这一个代码含义是不是呼之欲出了?
//此时nextval[j]的值就是就是t.data[j]不匹配时应该回溯到的字符的nextval值
//用较为粗鄙语言表诉:即字符不匹配时回溯两层后对应的字符下标}else k=nextval[k]; }}
int KMPIndex1(SqString s,SqString t)
//修正的KMP算法
//只是next换成了nextval
{int nextval[MaxSize],i=0,j=0;GetNextval(t,nextval);while (i<s.length && j<t.length) {if (j==-1 || s.data[i]==t.data[j]) { i++;j++; }else j=nextval[j];}if (j>=t.length) return(i-t.length);elsereturn(-1);
}
剩下的话
在写这篇博客时,我想起了编译原理老师讲过的一些知识,其实KMP算法的步骤与自动机有不少相似之处,有兴趣的朋友不妨联系对比一下。
参考书籍
《数据结构教程》(第5版) 李春葆
《大话数据结构》 程杰
---------------------
作者:哈顿之光
来源:CSDN
原文:https://blog.csdn.net/weixin_46007276/article/details/104372119
版权声明:本文为作者原创文章,转载请附上博文链接!
内容解析By:CSDN,CNBLOG博客文章一键转载插件

)
![[转]LVS负载均衡(LVS简介、三种工作模式、十种调度算法)](http://pic.xiahunao.cn/[转]LVS负载均衡(LVS简介、三种工作模式、十种调度算法))





![[转]Docker超详细基础教程,快速入门docker](http://pic.xiahunao.cn/[转]Docker超详细基础教程,快速入门docker)
)
)








