A Mysterious Function
| Time Limit: 1000MS | Memory Limit: 65536K | |
| Total Submissions: 3517 | Accepted: 2398 |
Description
For any integers p and q with q > 0, define p mod q to be the integer r with 0 <= r <= q −1 such that p−r is divisible by q. For example, we have
Let Φ be a function defined recursively as follows.
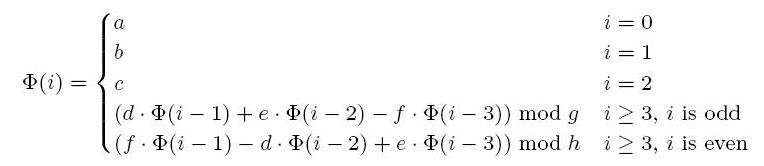
where a, b, c, d, e, f, g, h are integers with 0 < a, b, c, d, e, f, g, h <= 1000. One can easily see that 0 <= Φ(i) <= 1000 holds for any integer i >= 0. Now for any given integers a, b, c, d, e, f, g, h, i with 0 < a, b, c, d, e, f, g, h, i <= 1000, you are asked to write a program to output
Φ(i). (Hint: a direct recursive implementation of the above recurrence
relation is likely to run forever for large i.)
- 109 mod 10 = 9
- −7 mod 3 = 2
- −56 mod 7 = 0
Let Φ be a function defined recursively as follows.
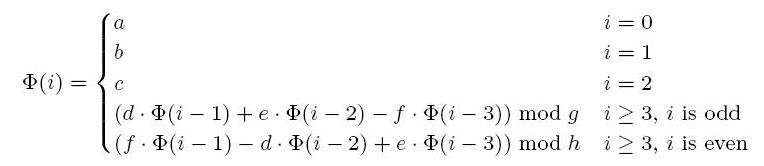
where a, b, c, d, e, f, g, h are integers with 0 < a, b, c, d, e, f, g, h <= 1000. One can easily see that 0 <= Φ(i) <= 1000 holds for any integer i >= 0. Now for any given integers a, b, c, d, e, f, g, h, i with 0 < a, b, c, d, e, f, g, h, i <= 1000, you are asked to write a program to output
Φ(i). (Hint: a direct recursive implementation of the above recurrence
relation is likely to run forever for large i.)
Input
The first line contains the number n of test cases. Each of the following n lines contains the sequence a, b, c, d, e, f, g, h, i of integers.
Output
For each test case, your program has to output the correct value of Φ(i).
Sample Input
3 1 2 3 4 5 6 7 8 9 11 12 13 14 15 16 17 18 19 321 322 323 324 325 326 327 328 329
Sample Output
4 0 90
#include<iostream>
using namespace std;
int mod(int a,int b)
{
int i;
for(i=0;i<=b-1;i++)
if((a-i)%b==0)
return i;
}
int main()
{
int n;
int res[1000];
int a,b,c,d,e,f,g,h,i;
int x;
cin>>n;
while(n--)
{
cin>>a>>b>>c>>d>>e>>f>>g>>h>>i;
res[0]=a;
res[1]=b;
res[2]=c;
x=3;
while(1)
{
if(x%2==1)
res[x]=mod((d*res[x-1]+e*res[x-2]-f*res[x-3]),g);
if(x%2==0)
res[x]=mod((f*res[x-1]-d*res[x-2]+e*res[x-3]),h);
if(x>=i)
break;
x++;
}
cout<<res[i]<<endl;
}
return 0;
}





)


)










