# -*- coding:utf-8 -*-
'''
@Author: 董咚咚
@contact: 2648633809@qq.com
@Time: 2023/7/31 17:02
@version: 1.0
'''
import requests
import reimport xlwt
from bs4 import BeautifulSoupurl = "https://www.dygod.net/html/gndy/dyzz/"
hd = {'user-Agent':'Mozilla/4.0 (Windows NT 10.0; Win64; x64) AppleWebKit/537.36 (KHTML, like Gecko) Chrome/95.0.4638.69 Safari/537.36'
}#linkurl = "https://www.dygod.net/html/gndy/dyzz/20230712/120036.html"
def getmanget(linkurl):res = requests.get(linkurl)res.encoding = res.apparent_encodingsoup = BeautifulSoup(res.text,"html.parser")ret = soup.find_all("a")for n in ret:if "magnet" in str(n.string):return n.stringreturn Nonedef insertDB():passdef saveExcel(worksheet,count,lst):for i in range(6):worksheet.write(count,i,lst[i])#代码正式开始
count = 0 #记录爬取电影的数量,每爬取一次,就在下面的列表里面添加一次
total = [] #用来储存记录信息的列表
workbook = xlwt.Workbook(encoding="utf-8")
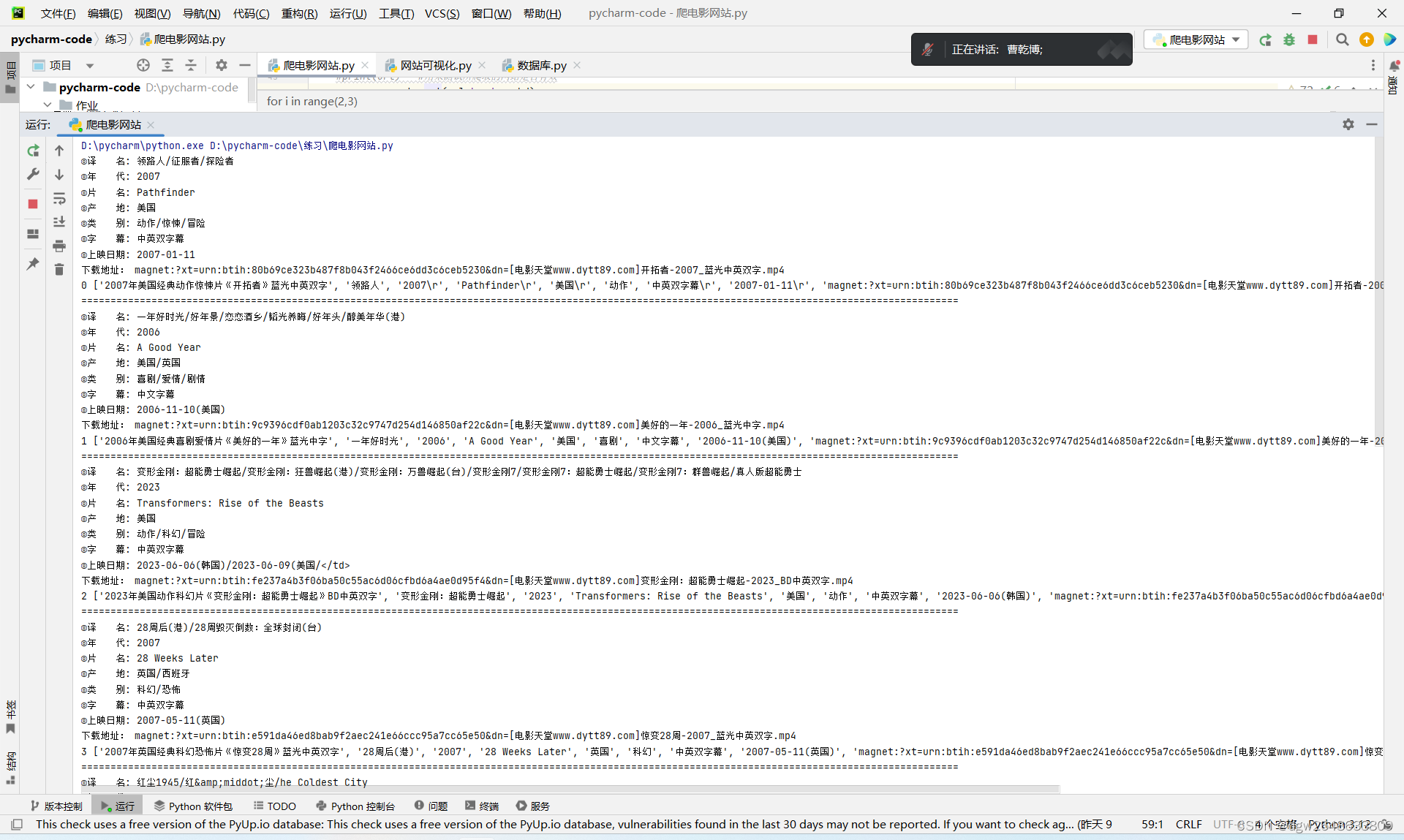
worksheet = workbook.add_sheet('sheet1')for i in range(2,3): #页面数量,就是从第二页到第八页,页数可以自己测试url = "https://www.dygod.net/html/gndy/dyzz/index_"+str(i)+".html"#print(url) #用来测试所爬取的网站是否有效res = requests.get(url,headers=hd)res.encoding = res.apparent_encoding#print(res.text) #获取相关和列表soup = BeautifulSoup(res.text,"html.parser")#print(soup.title,type(soup.title)) #查看电影的名字ret = soup.find_all(class_="tbspan",style = "margin-top:6px") #此内容都可以用Fn+F12查看,找到所有电影的表格for x in ret: #遍历每个电影的表格info = []#print(x.find("a").string) #打印除a标签的内容,即电影的名称info.append(x.find("a").string)pat = re.compile(r"◎译 名(.*)\n")ret = re.findall(pat,str(x))for n in ret:n = n.replace(u'\u3000',u'') #查看电影译名print("◎译 名:",n)info.append(str(n).split("/")[0])pat = re.compile(r"◎年 代(.*)\n")ret = re.findall(pat,str(x))for n in ret:n = n.replace(u'\u3000',u'')print("◎年 代:",n) #打印出相关的年代info.append(str(n))pat = re.compile(r"◎片 名(.*)\n")ret = re.findall(pat,str(x))for n in ret:n = n.replace(u'\u3000', u'')print("◎片 名:",n) #打印出相关的片名info.append(str(n).split("/")[0])pat = re.compile(r"◎产 地(.*)\n")ret = re.findall(pat,str(x))for n in ret:n = n.replace(u'\u3000', u'')print("◎产 地:",n) #打印出相关的片名info.append(str(n).split("/")[0])pat = re.compile(r"◎类 别(.*)\n")ret = re.findall(pat,str(x))for n in ret:n = n.replace(u'\u3000', u'')print("◎类 别:",n) #打印出相关的片名info.append(str(n).split("/")[0])pat = re.compile(r"◎字 幕(.*)\n")ret = re.findall(pat,str(x))for n in ret:n = n.replace(u'\u3000', u'')print("◎字 幕:",n) #打印出相关的片名info.append(str(n).split("/")[0])pat = re.compile(r"◎上映日期(.*)\n")ret = re.findall(pat,str(x))for n in ret:n = n.replace(u'\u3000', u'')print("◎上映日期:",n) #打印出相关的片名info.append(str(n).split("/")[0])linkurl = "https://www.dygod.net/" + x.find("a").get("href")manget = getmanget(linkurl)if manget:print("下载地址:",manget)info.append(str(manget))print(count,info)saveExcel(worksheet,count,info)count+=1print("="*150) #将列表转换成百分比的形式workbook.save("movie.xls")
print(count)






)




原理逻辑代码超详细!参考自《算法导论》)




)

————三轴加速度ADXL345使用(SPI方式))

