一、▽ 算子、点积、叉积
l▽ 算子叫“del”算子,即<< span="">∂/∂x,∂/∂y,∂/∂z>,可以理解为一个符号向量,向量里的元素是偏微分运算符号,没有任何具体意义,只是一个表示方法。
ln维向量的内积定义如下:
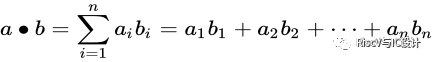
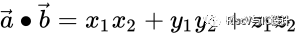 (常用的3维空间定义)
(常用的3维空间定义)
对于二维和三维空间,点积的几何定义为:
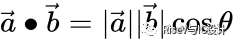
这个运算可以简单地理解为:在点积运算中,第一个向量投影到第二个向量上
l向量积,数学中又称外积、叉积,物理中称矢积、叉乘,是一种在向量空间中向量的二元运算。与点积不同,它的运算结果是一个向量而不是一个标量,其常见的各种定义如下:
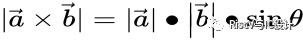


名称 | 标积/内积/数量积/点积 | 矢积/外积/向量积/叉积 |
运算式 | a·b=|a||b|·cosθ | a×b=c,其中|c|=|a||b|·sinθ,c的方向遵守右手定则 |
几何意义 | 向量a在向量b方向上的投影与向量b的模的乘积 | c是垂直a、b所在平面,且以|b|·sinθ为高、|a|为底的平行四边形的面积 |
运算结果的区别 | 标量(常用于物理)/数量(常用于数学) | 矢量(常用于物理)/向量(常用于数学) |
二、梯度、散度、旋度
有了▽算子,梯度、散度、旋度都可以用▽向量来表示。
1.梯度 gradient
函数f(x,y,z)(标量)的梯度可以理解为▽向量与函数f的乘积,即: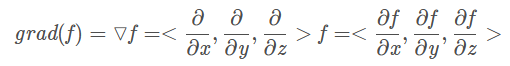

梯度的定义:在标量场f中的一点处存在一个矢量grad(f),该矢量方向为f在该点处变化率最大的方向,其模也等于这个最大变化率的数值,则矢量grad(f)称为标量场f的梯度。因此,梯度是矢量。
2.散度 divergence
散度可用于表征空间各点矢量场发散的强弱程度,物理上,散度的意义是场的有源性。当div F>0 ,表示该点有散发通量的正源(发散源);当div F<0 表示该点有吸收通量的负源(洞或汇);当div F=0,表示该点无源。
散度可以表示为▽向量与矢量场F的点积,散度是标量:
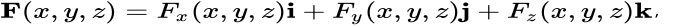
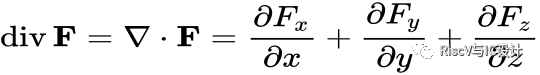
l运算法则
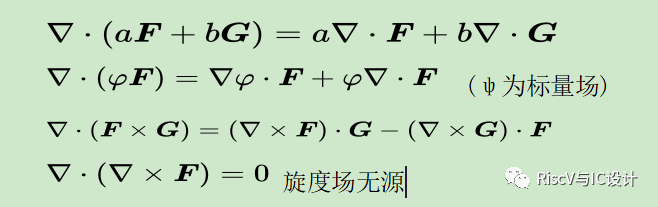
l不同坐标系下的散度表达式
矢量V的散度在笛卡尔坐标(直角坐标系)下的表达式:
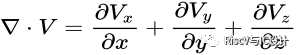
矢量V的散度在球坐标下的表达式:
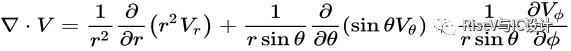
矢量V的散度在柱坐标下的表达式:
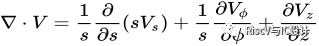
3.旋度 curl
定义向量场的旋度,首先要引入环量(或称为旋涡量)的概念。给定一个三维空间中的向量场u以及一个简单闭合有向(平面)曲线L,u沿着曲线的环量就是u沿着路径的闭合曲线L的点积的积分:
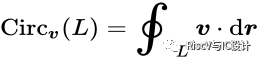
其中曲线上的线元 dr是矢量,方向是曲线的切线方向,其正方向规定为使得闭合曲线所包围的面积在它的左侧。
环量和通量一样,是描述向量场的重要参数。某个区域中的环量不等于零,说明这个区域中的向量场表现出环绕某一点或某一区域旋转的特性。旋度则是局部地描述这一特性的方法。为了描述一个向量场在一点附近的环量,将闭合曲线收小,使它包围的面元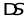 的面积趋于零。向量场u沿着L的环量和面元的比值在趋于零时候的极限值:
的面积趋于零。向量场u沿着L的环量和面元的比值在趋于零时候的极限值:
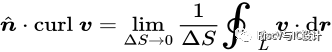
 为
为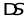 的所在平面的法向量
的所在平面的法向量
向量场的旋度记作: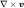
l直角坐标系
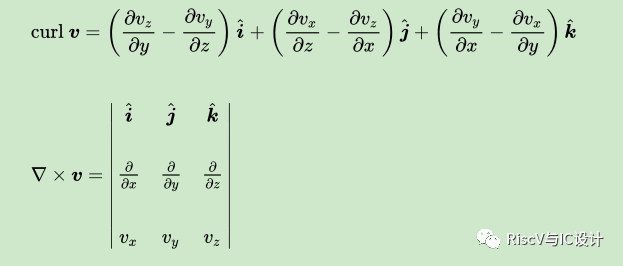
l圆柱坐标系
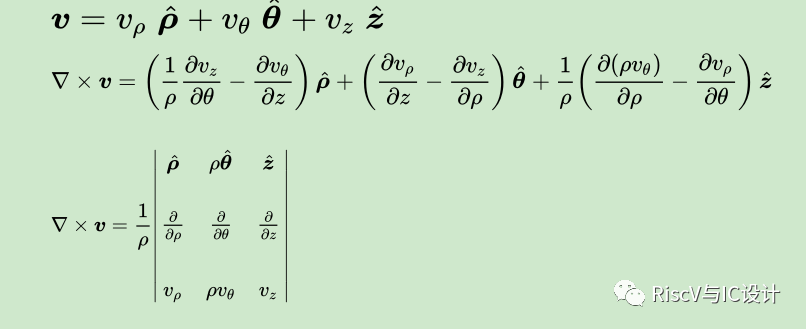
l球坐标系
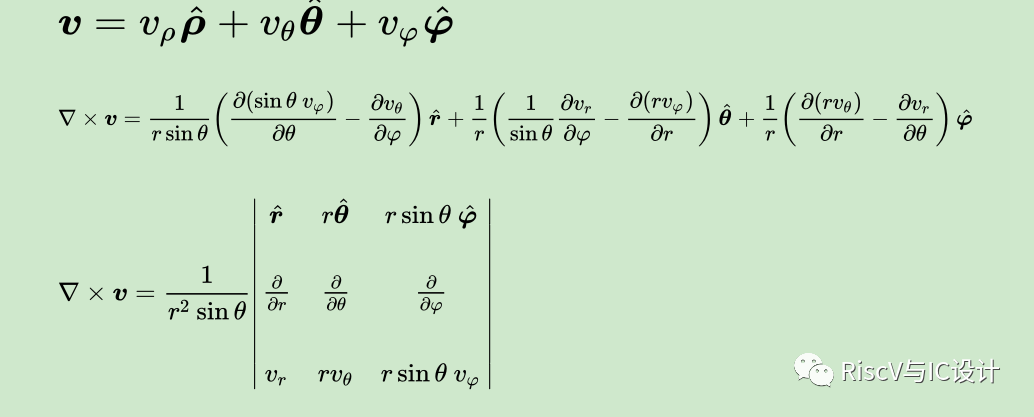
三、线积分、面积分、散度定律、斯托克斯定理
l线积分
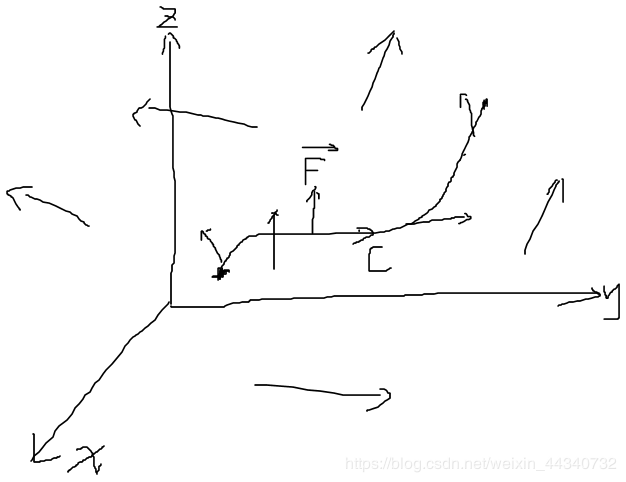
上图中,F是空间中的矢量场, C是含有方向的线段。则 F对C的积分(理解为物理上的功)可以表示为:
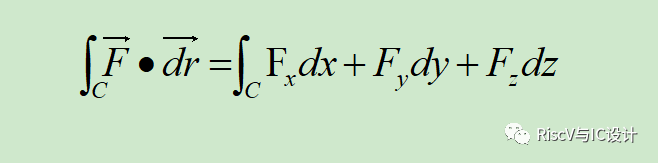
l面积分
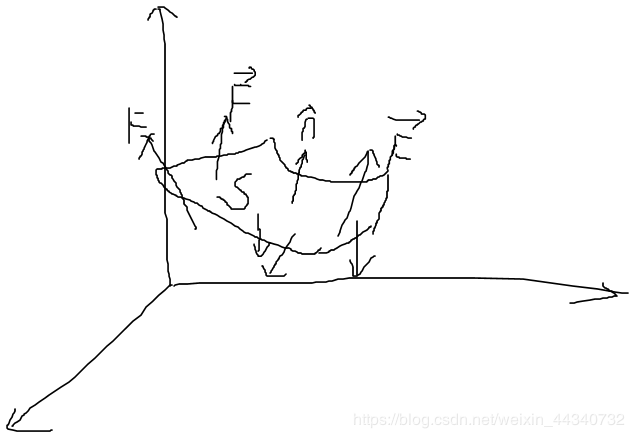
上图中,S表示空间中一个曲面,nˆ表示曲面的法向量(两个方向中选一个)。则矢量 F对曲面S的积分表示通量(Flux),即: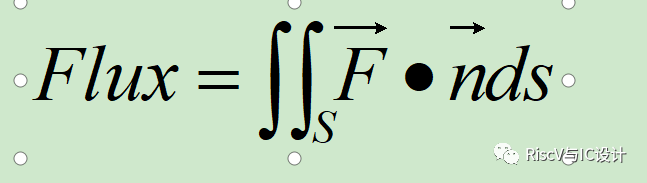
lGauss-Green 定理(散度定理)
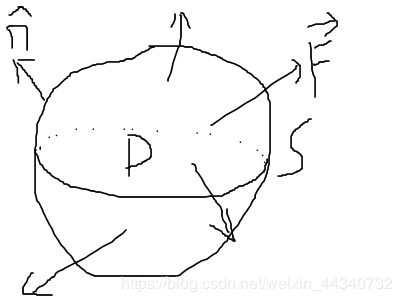
如果S是空间中的封闭曲面,包裹了一个区域D,法向量nˆ
n^向外, F在D的每一个区域都定义且可微,则下式成立: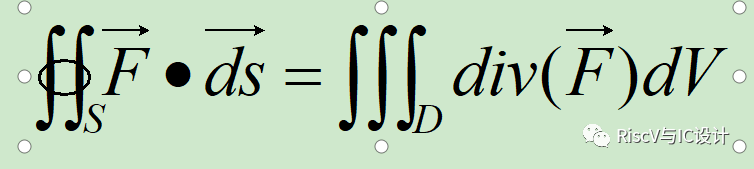
l斯托克斯定理(Stokes)定理
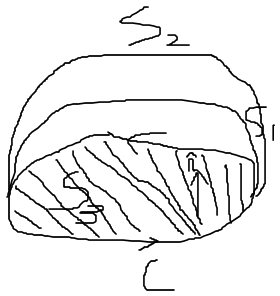
如果C是一个封闭曲线,S是以C为边的任意曲面,F在S上有定义,nˆ为满足右手定则方向向外,则有如下公式: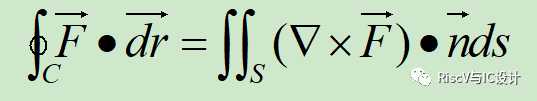
四、麦克斯韦方程组
1. 积分形式的麦克斯韦方程组是描述电磁场在某一体积或某一面积内的数学模型。表达式为:
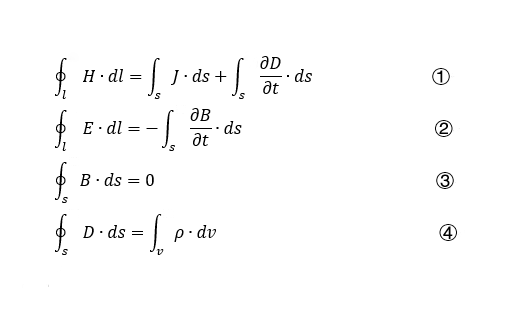
l式①是由安培环路定律推广而得的全电流定律,其含义是:磁场强度H沿任意闭合曲线的线积分,等于穿过此曲线限定面积的全电流。等号右边第一项是传导电流.第二项是位移电流。
l式②是法拉第电磁感应定律的表达式,它说明电场强度E沿任意闭合曲线的线积分等于穿过由该曲线所限定面积的磁通对时间的变化率的负值。这里提到的闭合曲线,并不一定要由导体构成,它可以是介质回路,甚至只是任意一个闭合轮廓。
l式③表示磁通连续性原理,说明对于任意一个闭合曲面,有多少磁通进入曲面就有同样数量的磁通离开。即B线是既无始端又无终端的;同时也说明并不存在与电荷相对应的磁荷。
l式④是高斯定律的表达式,说明在时变的条件下,从任意一个闭合曲面出来的D的净通量,应等于该闭曲面所包围的体积内全部自由电荷之总和。
2. 微分形式的麦克斯韦方程组。微分形式的麦克斯韦方程是对场中每一点而言的。应用del算子,可以把它们写成
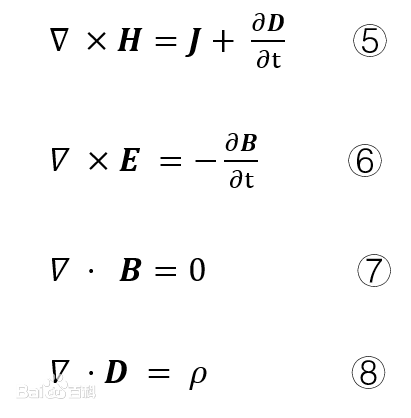
l式⑤是全电流定律的微分形式,它说明磁场强度H的旋度等于该点的全电流密度(传导电流密度J与位移电流密度之和),即磁场的漩涡源是全电流密度,位移电流与传导电流一样都能产生磁场。
l式⑥是法拉第电磁感应定律的微分形式,说明电场强度E的旋度等于该点磁通密度B的时间变化率的负值,即电场的涡旋源是磁通密度的时间变化率。
l式⑦是磁通连续性原理的微分形式,说明磁通密度B的散度恒等于零,即B线是无始无终的。也就是说不存在与电荷对应的磁荷。
l式⑧是静电场高斯定律的推广,即在时变条件下,电位移D的散度仍等于该点的自由电荷体密度。
除了上述四个方程外,还需要有媒质的本构关系式,才能最终解决场量的求解问题。式中ε是媒质的介电常数,μ是媒质的磁导率,σ是媒质的电导率:
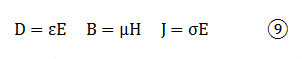
麦克斯韦方程组表格:
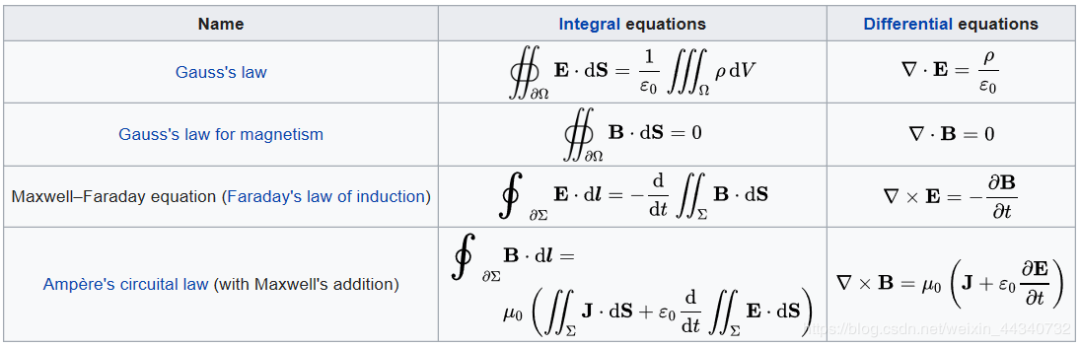
、Handler类、安卓Socket传数据、WebView)


















